
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стационарные случайные процессыСодержание книги
Поиск на нашем сайте
В стационарном случайном процессе закон распределения один и тот же для каждого момента времени, т.е. w x (x, t) – не зависит от времени т.е. w(x, t) = w(t). (2.7) Следовательно mx (t) = mx = const, s x (t) = s x = const вдоль всего процесса. Пример: колебание напряжения и тока в установившемся режиме электрической цепи. Следует заметить, что если mx (t) ¹ const, а s x (t) = s x = const для ряда задач такая нестационарность несущественна, т.к. можно перейти к центрированному случайному процессу:
1) ограничиваясь только стационарными процессами, можно определить только установившиеся (стационарные) динамические ошибки автоматических систем при случайных воздействиях. (По аналогии с исследованием динамических свойств систем в установившемся режиме); 2) эргодическое свойство стационарных случайных процессов (эргодическая гипотеза): стационарный процесс обладает эргодическим свойством, если для него среднее значение по множеству наблюдений (множеству реализаций) равно среднему значению по времени наблюдения (по длине реализации) т.е. среднее по множеству равно среднему по времени.
Следовательно, математическое ожидание для любого ti
Аналогичным образом могут быть определены и моменты более высоких порядков: D, τ и т.д. Эргодическая гипотеза значительно упрощает многие расчёты и эксперименты. Так вместо одновременного испытания многих систем в один момент времени можно испытывать систему в течение длительного времени. Таким образом, одна реализация стационарного случайного процесса на бесконечном (большом) промежутке времени полностью определяет весь процесс со всеми бесконечными его реализациями. Заметим, что этим свойством не обладают другие случайные процессы. Преобразования случайных функций. Сложение случайных функций. При сложении случайных функций, в общем случае, с произвольными постоянными коэффициентами а и b, и образовании случайной функции суммы Z(t) = aЧ X(t) + bЧ Y(t) функция математического ожидания процесса Z(t): mz(t)= M{Z(t)}= M{aX(t)+bY(t)}= aЧ M{X(t)}+bЧ M{Y(t)}= aЧ mx(t)+bЧ my(t). Корреляционная функция суммы вычисляется аналогично и равна:
Rz(t1,t2) = M{Z(t1)Ч Z(t2)}= M{[aX(t1)+bY(t1)][(aX(t2)+bY(t2)]}= = M{a2X(t1)X(t2)+b2Y(t1)Y(t2)+Ч ab[X(t1)Y(t2)+Y(t1)X(t2)]} = a2Rx(t1,t2)+b2Ry(t1,t2)+abЧ [Rxy(t1,t2)+Ryx(t1,t2)]. Для некоррелированных функций X(t) и Y(t) функции взаимной корреляции Rxy и Ryx обнуляются. Аналогичную форму записи имеют и ковариационные функции (как частный случай корреляционных функций при центрировании случайных процессов). Выражения легко обобщаются на сумму любого числа случайных функций. В частности, для корреляционной функции стационарной случайной функции Z(t) = При сложении случайной функции X(t) с неслучайной функцией y(t) математическое ожидание и корреляционная функция суммы Z(t)=X(t)+y(t) равны: mz(t) = mx(t) + y(t), Rz(t1,t2) = Rx(t1,t2). При сложении случайной функции X(t) с некоррелированной случайной величиной Y математическое ожидание и корреляционная функция суммы Z(t)=X(t)+Y: mz(t) = mx(t) + my, Rz(t1,t2) = Rx(t1,t2) + Dy. Произведение случайной и неслучайной функций X(t) и f(t). Математическое ожидание и корреляционная функция выходного сигнала: mz(t) = M{Z(t)}= M{f(t)Ч X(t)}= f(t)Ч M{X(t)}= f(t)Ч mx(t) Rz(t1,t2)=M{f(t1)X(t1) f(t2)X(t2)}= f(t1)f(t2)M{X(t1)X(t2)}= f(t1)f(t2)Ч Rx(t1,t2). Если f(t) = const = C и Z(t) = CЧ X(t), то соответственно имеем: mz(t) = СЧ mx(t), Rz(t1,t2) = С2Ч Rx(t1,t2). Производная от случайной функции Z(t) = dX(t)/dt. Если функция X(t) является непрерывной и дифференцируемой, то математическое ожидание производной: mz(t) = M{Z(t)} = M{dX(t)/dt} = d(M{X(t)})/dt = dmx(t)/dt т.е. математическое ожидание производной от случайной функции равно производной от ее математического ожидания. Для корреляционной функции имеем: Rz(t1,t2)=M{(dX(t1)/dt1)(dX(t2)/dt2)}= Интеграл от случайной функции Z(t) = mz(t)=M{Z(t)}=M{ т.е. математическое ожидание интеграла от случайной функции равно интегралу от ее математического ожидания. Для корреляционной функции имеем: Rz(t1,t2)=M{ Преобразования стационарных случайных функций выполняются по вышеприведенным формулам и приводят к следующим результатам (вместо корреляционных функций приводятся ковариационные функции, которые обычно используются на практике).
Математическое ожидание выходного сигнала Z(t) входной стационарной случайной функции X(t) по mz = h(t) * mx = mx Отсюда следует, что математическое ожидание выходных сигналов системы равно математическому ожиданию входных сигналов, умноженному на площадь (или сумму коэффициентов) импульсного отклика системы, т.е. на коэффициент усиления системой постоянной составляющей. Если система не пропускает постоянную составляющую сигналов (площадь или сумма коэффициентов импульсного отклика системы равна нулю), то случайный выходной сигнал всегда будет иметь нулевое математическое ожидание. Сумма двух стационарных случайных функций X(t) и Y(t) дает стационарную случайную функцию Z(t), при этом: mz = mx + my, Dz = Dx + Dy + 2Kxy(0). Kz(t1,t2) = Kz(t) = Kx(t) + Ky(t) + Kxy(t) + Kyx(t) Сумма стационарной случайной и неслучайной функций X(t) и y(t) нестационарна по математическому ожиданию: mz(t) = mx + y(t), Kz(t) = Kx(t). Произведение стационарной случайной и неслучайной функций X(t) и y(t) -нестационарная случайная функция, так как: mz(t) = y(t)Ч mx, Dz(t) = y2(t)Ч Dx. Kz(t,t) = y(t)y(t+t)Kx(t). Производная от стационарной случайной функции - стационарная случайная функция с математическим ожиданием mz = 0 и ковариационными функциями: Kz(t1,t2) = Kzx(t) = d(Kx(t))/dt, Kxz(t) = -d(Kx(t))/dt. (9.3.33) Из выражения (17.3.32) следует также, что для дифференцируемости X(t) необходимо, чтобы ее ковариационная функция была дважды дифференцируемой по t. Интеграл от стационарной случайной функции - нестационарная случайная функция с математическим ожиданием mz(t) = Спектральное разложение Стационарный случайный процесс может быть представлен каноническим разложением вида:
где Vk и Uk –некоррелированные и центрированные случайные величины с дисперсиями D [ Vk ] = D [ Uk ] = Dk; w – неслучайная величина (частота). В этом случае каноническое разложение корреляционной функции определяется выражением
Каноническое разложение называется спектральным разложением стационарного случайного процесса. Спектральное разложение может быть также представлено в виде
где qk – фаза гармонического колебания элементарного стационарного случайного процесса, являющаяся случайной величиной равномерно распределенной в интервале (0, 2 p); Zk – амплитуда гармонического колебания элементарного стационарного случайного процесса – тоже случайная величина. Случайные величины qk и Zk зависимы. Для них имеют место соотношения:
Таким образом, стационарный случайный процесс может быть представлен в виде суммы гармонических колебаний со случайными амплитудами Zk и случайными фазами qk на различных неслучайных частотах wk. Так как корреляционная функция стационарного случайного процесса X (t) является четной функцией своего аргумента, т. е. kx (t) = kx (–t), то ее на интервале (– T, T) можно разложить в ряд Фурье по четным (косинусам) гармоникам
Подставляя в выражение (6.45) t = 0, получим каноническое разложение для дисперсии стационарного случайного процесса:
Таким образом, дисперсия стационарного случайного процесса, представленная своим каноническим разложением, равна сумме дисперсий всех гармоник его спектрального разложения.
Используя формулы при k = 1, 2, 3, …, можно построить график изменения дисперсий Dk по частотам wk (рис.6.7). Зависимость Dk = f (wk)в этом случае называется дискретным спектром дисперсий или просто – дискретным спектром стационарного случайного процесса.
Рис.6.7. Дискретный спектр стационарного случайного процесса. В пределе, при В качестве характеристики распределения дисперсии по частотам непрерывного спектра используется спектральная плотность – Sx (w), которую можно рассматривать, как предел отношения дисперсии приходящейся на каждую частоту к D w:
1. Она является неотрицательной функцией частоты:
2. Интеграл от спектральной плотности в пределах от 0 до ∞ равен дисперсии стационарного случайного процесса: Нормированная корреляционная функция и нормированная спектральная плотность также связаны между собой преобразованием Фурье Интеграл от нормированной спектральной плотности в пределах от 0 до ∞ равен единице:
Таблица 6.1 Различные определения спектральной плотности Спектральная плотность
Корреляционная функция
При аналитических расчетах нередко используется спектральная плотность в комплексной форме Спектральная плотность в комплексной форме обладает следующими свойствами: 1.
2. Интеграл от
Пара преобразований Фурье для корреляционной функции и спектральной плотности в комплексной форме имеет вид:
Следует отметить, что если спектральную плотность для действительных случайных процессов рассматривать как часть спектральной плотности 19.Основные статистические описания. Вариационный ряд и эмпирические квантили. Распределение частот. Эмпирический коэффициент корреляция. Межгрупповая дисперсия. Ряды распределения, построенные по количественному признаку (возраст, стаж, сроки расследования или рассмотрения дел, число судимостей и т.д.), называются вариационными рядами. Различия единиц совокупности (до 20 лет, 20-24 года, 25-29 лет и т.д.) количественного признака называется вариацией, а сам конкретный признак – вариантой. Вариация признаков может быть дискретной, или прерывной (20, 21, 22, 23, 24, 25 лет и т.д.), либо непрерывной (до 20 лет, 20-25, 25-30 лет и т.д.). При дискретной вариации величина количественного признака (варианты) может принимать вполне определенные значения, отличающиеся в нашем примере на 1 год (20,21,22 и т.д.). При непрерывной вариации величина количественного признака у единиц совокупности в определенном численном промежутке (интервале) может принимать любые значения, хоть сколько-нибудь отличающиеся друг от друга. Например, в интервале 20-25 лет возраст конкретных сотрудников может быть 20 лет и 2 дня, 21 год и 10 месяцев и т.д. Вариационные ряды, построенные по дискретно варьирующим признакам, именуют дискретными вариационными рядами, а построенные по непрерывно варьирующим признакам (интервалам) – интервальными вариационными рядами. Вариационный ряд всегда состоит из двух основных граф (колонок) цифр. В первой колонке указываются значения количественного признака в порядке возрастания. В нашем примере интервального вариационного ряда: до 20 лет, 20-24 года, 25-29 лет и т.д. При дискретной вариации 20, 21, 22, 23, 24, 25 лет. Эти значения количественного признака и называют вариантами. В статистической литературе этот термин иногда употребляется как существительное мужского рода (вариант, варианты), а иногда – как существительное женского рода (варианта, варианты). Во второй колонке указываются числа единиц, которые свойственны той или иной варианте. Их называют частотами, если они выражены в абсолютных числах, т.е. сколько раз в изучаемой совокупности встречается та или иная варианта, или частостями, если они выражены в удельных весах или долях, т.е. в процентах или коэффициентах к итогу. Интервальный вариационный ряд иногда строится с равными интервалами (20-24, 25-29 лет), а иногда с неравными (14-15, 16-18, 19-20, 21-25 лет) интервалами. В первом случае оба интервала равны 5 годам, а во втором случае – 2, 3, 5 годам. При построении интервального ряда с непрерывной вариацией верхняя граница каждого интервала обычно является нижней границей последующего (20-25, 25-30, 30-35 и т.д.), а в построении интервального ряда по дискретному признаку границы смежных интервалов не повторяются (1-5 дней, 6-10 дней, 11-15 дней и т.д.)
Статистический анализ вариационных рядов требует не только наличия единичных частот (частостей), но и накопленных частот (частостей). Накопленная частота для той или иной варианты представляет собой сумму частот всех предшествующих вариант (интервалов). В нашем примере (табл. 1) для интервала 20-24 года накопленная частота будет равна: Вариационные ряды легко изображаются графически в виде полигона или гистограммы. Графическое изображение накопленных частот (частостей) воспроизводится в системе прямоугольных координат в виде кумуляты, или кумулятивной кривой. По оси ординат откладывается величина накопленных частот, а по оси абсцисс – возрастающие значения количественного признака. Накопленные частоты и кумулята – это интегральные показатели плотности распределения в вариационном ряду. Квантили и процентные точки распределения.При использовании различных методов математической статистики, особенно разнообразных статистических критериев методов построения интервальных оценок неизвестных параметров широко используются понятия -квантилей и -процентных точек распределения Квантилью уровня q (или -квантилью) непрерывной случайной величины обладающей непрерывной функцией распределения называется такое возможное значение этой случайной величины, для которого вероятность события равна заданной величине q, т. е.
Очевидно, чем больше заданное значение тем больше будет и соответствующая величина квантили Частным случаем квантили — -квантилью является характеристика центра группирования — медиана. Для всякой дискретной случайной величиныфункция распределения с увеличением аргумента меняется, как мы видели, скачтми, и, следовательно, существуют такие значения уровней q, для каждого из которых не найдется возможного значения точно удовлетворяющего уравнению Эмпирическими аналогами теоретических квантилей, как легко понять, будут члены вариационного ряда (порядковые статистики). Из их определения, в частности, следует что порядковая статистика является одновременно выборочной квантилью уровня. Часто вместо понятия квантили используют тесно связанное с ним понятие процентной точки. Под -процентной точкой случайной величины понимается такое ее возможное значение для которого вероятность события равна т. е. Для дискретных случайных величин это определение корректируется аналогично тому, как это делалось при определении квантилей. Из определения квантилей и процентных точек вытекает простое соотношение, их связывающее:
Для ряда наиболее часто встречающихся в статистической практике законов распределения составлены специальные таблицы квантилей и процентных точек. Очевидно, достаточно иметь только одну из таких таблиц, так как если, например, по таблицам процентных точек требуется найти -квантиль нормального распределения, то следует искать, в соответствии с (5.32), -процентную точку того же распределения. Наглядное геометрическое представление о смысле введенных понятий дает рис. 5.10. Здесь. Квантильные характеристики помимо своей основной роли вспомогательного теоретического статистического инструментария порой играют самостоятельную роль основных характеристик изучаемого закона распределения или содержательно интерпретируемых параметров модели. Так, широко распространенной характеристикой степени случайного рассеяния при изучении законов распределения заработной платы и доходов являются так называемые квантильные (уровня q) коэффициенты дифференциации которые определяются соотношением
При анализе модельных законов распределения квантили и процентные точки используют также для обозначения практических границ диапазона изменения исследуемого признака: так, например, квантилями уровня 0,005 и 0,995 иногда определяют соответственно минимальный и максимальный уровни заработной платы работников в соответствующей системе показателей. Частотное распределение — метод статистического описания данных (измеренных значений, характерных значений). Математически распределение частот является функцией, которая в первую очередь определяет для каждого показателя идеальное значение, так как эта величина обычно уже измерена. Такое распределение можно представить в виде таблицы или графика, моделируя функциональные уравнения. В описательной статистике частота распределения имеет ряд математических функций, которые используются для выравнивания и анализа частотного распределения (например, нормальное распределение распределение Гаусса). Объём данных (измеренные значения, данные обследования) является первым оригинальным неупорядоченным списком. Во-первых, его необходимо отсортировать. От первоначального списка, в этом случае, может возникнуть небольшое отклонение квантилей (статистический разброс), вероятного отклонения и стандартного отклонения (эмпирическое правило: стандартное отклонение = расстояние / 6). Затем мы приписываем каждой величине значение и суммируем их. Как правило мы получаем абсолютную частоту. Опираясь на данные абсолютной частоты вычисляем общее количество значений выборки и вычисляем относительные частоты. Теперь у нас есть упорядоченное множество пар значений (характерные значения и связанных с ними относительные частоты), так называемый рейтинг. Добавим относительные частоты, начиная с наименьшего значения признака и назначим каждой функции значение суммы (в том числе его собственного вклада), так чтобы получилось распределение. Это указывает для каждого значения признака, насколько велика его доля, меньших или равных соответствующего характеристического значения. Процент начинается с 0 и приближается к 1 или 100 процентам. Графически это изображается слабой монотонно возрастающей кривой, имеющей удлиненную S-образную форму. Существуют многочисленные попытки воспроизведения результатов распределения функциональными уравнениями. Распределение суммы, в зависимости от значений признаков самый простой тип представления распределения частот. По правилам также необходимо произвести классификацию характерных значений. Эта процедура делит диапазон значений, возникающих, например, в 10 или 20 одинаковой ширины классов (редких значений по краям (см. «выбросы») иногда группирующихся вместе в большими классами). Затем определяется плотность функции, производной функции распределения в соответствии с характеристикой значения в случае непрерывного распределения. Кроме того, частоту можно определить не только путём подсчета, но также, например, путём взвешивания. Тогда мы получим распределение массы вместо ряда распределения. В принципе, можно воспользоваться любой аддитивной величиной для измерения частоты. Если случайная выборка сильно отличается от нормального распределения (кривой нормального распределения), то данные могут быть смещены с помощью выбора эффектов или тенденций. Различные статистические тесты предлагают вывод или дисперсионный анализ. Если размер выборки находится в суперпозиции нескольких подмножеств (возрастное распределение, профессий, групп), то распределение частот вместо максимальных также может быть двух-или многомерным. Коэффициент Корреляции Коэффициентом корреляции r между случайными величинами x и y называется математическое ожидание произведения их нормированных отклонений:
Коэффициент корреляции r может быть также записан в одной из следующих форм:
Коэффициент корреляции представляет собой безразмерную величину, лежащую в пределах:
Несмещенными и состоятельными оценками средних значений a и b служат эмпирические средние значения:
Наконец, несмещенной и состоятельной оценкой корреляционного момента служит эмпирический корреляционный момент:
Если весь диапазон изменения величины x разбит на интервалы равной длины, также как и весь диапазон изменения величины y, то результаты измерений удобно записывать в виде корреляционной таблицы (“корреляционной решетки”). В каждую клетку корреляционной таблицы проставляется только число измерений, результаты которых попали в данную клетку, а в заглавных строке и столбце указываются середины соответствующих интервалов. При этом и весь расчет удобно проводить в той же корреляционной таблице. Поскольку здесь мы имеем дело с интервальными рядами, то в качестве масштабных коэффициентов Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней: 20.Интервальные хар-ки признака. Повторные и бесповторные выборки. Выборочная доля признака. Пропорциональная выборка.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.124 (0.014 с.) |

 ,который будет стационарным, т.к.
,который будет стационарным, т.к. 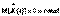 . Отсюда следуют важные практические свойства:
. Отсюда следуют важные практические свойства: аРис. 2.4. Случайный процесс обладает (а), и не обладает (б)эргодическим свойством
аРис. 2.4. Случайный процесс обладает (а), и не обладает (б)эргодическим свойством бРис. 2.4. Окончание
бРис. 2.4. Окончание .
. aiXi(t) при t2-t1 = t имеем: Rz(t) =
aiXi(t) при t2-t1 = t имеем: Rz(t) =  ai2Rxi(t) +
ai2Rxi(t) +  aiajRxixj(t).
aiajRxixj(t). M{X(t1)X(t2)}=
M{X(t1)X(t2)}=  X(v)dv.
X(v)dv. X(v)dv}=
X(v)dv}=  mx(v)dv, (17.3.24)
mx(v)dv, (17.3.24) M{X(t1)X(t2)}dt1dt2]=
M{X(t1)X(t2)}dt1dt2]=  h(t) dt
h(t) dt Kx(t1-t2) = -
Kx(t1-t2) = -  Kx(t) = Kz(t). (17.3.32)
Kx(t) = Kz(t). (17.3.32) mx(t)dt и функцией ковариации:Kz(t1,t2) =
mx(t)dt и функцией ковариации:Kz(t1,t2) = 
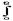 Kx(u1-u2) du1du2.
Kx(u1-u2) du1du2. ,
, ,
, ,
, ,
,  .
.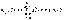 , где wk и Dk определяются выражениями:
, где wk и Dk определяются выражениями: ,
,  , (6.46)
, (6.46)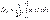 ,
,  .
. .
. (т. е. при
(т. е. при  ) мы перейдем к непрерывному спектру.
) мы перейдем к непрерывному спектру. . В этом случае выражение примет вид:
. В этом случае выражение примет вид: . Таким образом, корреляционная функция и спектральная плотность стационарного случайного процесса связаны косинус-преобразованием Фурье. Следовательно, спектральная плотность стационарного случайного процесса может быть выражена через корреляционную функцию по формуле
. Таким образом, корреляционная функция и спектральная плотность стационарного случайного процесса связаны косинус-преобразованием Фурье. Следовательно, спектральная плотность стационарного случайного процесса может быть выражена через корреляционную функцию по формуле .Спектральная плотность обладает следующими свойствами.
.Спектральная плотность обладает следующими свойствами. . (6.53)
. (6.53) . По аналогии с нормированной корреляционной функцией вводится нормированная спектральная плотность:
. По аналогии с нормированной корреляционной функцией вводится нормированная спектральная плотность:  . (6.55)
. (6.55) ,
, 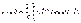 . (6.57)
. (6.57) . Таким образом, если на графике нормированной спектральной плотности (рис.6.8) рассматривать полосу частот от w 1 до w 2, то площадь подграфика, заключенная в интервале от w 1 до w 2, будет равна доле дисперсии случайного процесса, приходящейся на эти частоты. При этом общая площадь подграфика будет равна единице.
. Таким образом, если на графике нормированной спектральной плотности (рис.6.8) рассматривать полосу частот от w 1 до w 2, то площадь подграфика, заключенная в интервале от w 1 до w 2, будет равна доле дисперсии случайного процесса, приходящейся на эти частоты. При этом общая площадь подграфика будет равна единице.







 . В этом случае рассматриваются как положительные, так и отрицательные частоты, а
. В этом случае рассматриваются как положительные, так и отрицательные частоты, а  и S (w) связаны соотношением:
и S (w) связаны соотношением: 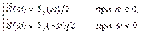
 является неотрицательной функцией частоты, то есть:
является неотрицательной функцией частоты, то есть: .
. в бесконечных пределах равен дисперсии случайного процесса:
в бесконечных пределах равен дисперсии случайного процесса: . 3.
. 3.  .
. ,
,  .
. , лежащую в области положительных частот, то мы получим определение S (w), приведенное в строке 2 таблицы 6.1. Однако в этом случае интеграл от нормированной спектральной плотности будет равен 0.5, а не единице, что с формальной точки зрения не очень хорошо.
, лежащую в области положительных частот, то мы получим определение S (w), приведенное в строке 2 таблицы 6.1. Однако в этом случае интеграл от нормированной спектральной плотности будет равен 0.5, а не единице, что с формальной точки зрения не очень хорошо.



 Геометрическое пояснение смысла -квантили и -ной точки случай стандартного нормального распределения, (соответственно) соответственно)
Геометрическое пояснение смысла -квантили и -ной точки случай стандартного нормального распределения, (соответственно) соответственно) , где
, где  ,
,  – центры распределения величин x и y;
– центры распределения величин x и y;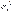 и
и  – их дисперсии.
– их дисперсии. . Величина
. Величина  называется корреляционным моментом или ковариацией.
называется корреляционным моментом или ковариацией. . Для независимых x и y коэффициент корреляции
. Для независимых x и y коэффициент корреляции  . Равенство
. Равенство  говорит о наличии линейной функциональной зависимости между величинами x и y (т.е. означает, что каждому значению одной величины соответствует только одно значение другой величины): для возрастающей функции
говорит о наличии линейной функциональной зависимости между величинами x и y (т.е. означает, что каждому значению одной величины соответствует только одно значение другой величины): для возрастающей функции  , для убывающей функции
, для убывающей функции 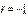 .Для экспериментального изучения зависимости между двумя величинами x и y производят некоторое количество n независимых испытаний (опытов, наблюдений). Результат i -го испытания дает пару значений
.Для экспериментального изучения зависимости между двумя величинами x и y производят некоторое количество n независимых испытаний (опытов, наблюдений). Результат i -го испытания дает пару значений  (
( ). По этим значениям определяются точечные оценки как средних значений, так и коэффициента корреляции.
). По этим значениям определяются точечные оценки как средних значений, так и коэффициента корреляции. ,
,  . Несмещенными и состоятельными оценками дисперсий
. Несмещенными и состоятельными оценками дисперсий  и
и  служат эмпирические дисперсии:
служат эмпирические дисперсии: (5)
(5) . По этим оценкам рассчитывают эмпирический коэффициент корреляции:
. По этим оценкам рассчитывают эмпирический коэффициент корреляции: . Эмпирический коэффициент корреляции не изменяется при изменении начала отсчета и масштаба измерения величин x и y. Это свойство позволяет существенно упростить вычисления с помощью выбора удобного начала отсчета
. Эмпирический коэффициент корреляции не изменяется при изменении начала отсчета и масштаба измерения величин x и y. Это свойство позволяет существенно упростить вычисления с помощью выбора удобного начала отсчета  и подходящих единиц масштаба: после замены
и подходящих единиц масштаба: после замены ,
,  (
( ,
,  ), т.е.
), т.е.  ,
,  , эмпирический коэффициент корреляции вычисляется по формуле:
, эмпирический коэффициент корреляции вычисляется по формуле: , где
, где 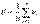 ,
,  .
. следует выбирать длины соответствующих интервалов. При этом в новых переменных u и v середины интервалов оказываются просто номерами интервалов, отсчитываемыми от некоторого интервала.
следует выбирать длины соответствующих интервалов. При этом в новых переменных u и v середины интервалов оказываются просто номерами интервалов, отсчитываемыми от некоторого интервала.



