
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы дисперсионного анализаСодержание книги
Поиск на нашем сайте
Дисперсионный анализ является одним из методов изучения влияния одного или нескольких факторных признаков на результативный признак. В зависимости от количества факторов дисперсионный анализ подразделяется на однофакторный и многофакторный. Ниже рассмотрено применение дисперсионного анализа для случая однофакторного комплекса.В основе дисперсионного анализа лежит расчленение общей вариации изучаемого признака по источникам ее происхождения на два вида вариации: •систематическую вариацию, которая обусловлена изменением признака-фактора;•остаточную (случайную) вариацию, обусловленную действием прочих, случайных, не связанных с данным фактором обстоятельств. Для разграничения этих вариаций всю совокупность наблюдавшихся единиц разбивают на группы (классы) по факторному признаку и исчисляют средние результативного признака по группам. Групповые средние где xi - индивидуальные значения признака в группе; ni - число единиц, входящих в группу; п - общее число наблюдений.Если сравнение групповых средних показывает определенное различие в их уровне, то необходимо установить, является ли это различие существенным и вызвано ли оно влиянием признака-фактора.Для ответа на поставленный вопрос определяют два показателя дисперсии:1) показатель
Эконометрические модели описывают взаимообусловленное развитие социально-экономических процессов на основе информации, отражающей распределение их уровней во времени и в пространстве однородных объектов. Наиболее важной задачей является оценка и проверка экономической модели. Эконометрическое моделирование охватывает весь цикл решения экономической задачи – от ее постановки до содержательной интерпретации результатов статистического анализа и прогнозирования. Классификация переменных в эконометрических моделях.1. Эндогенные переменные, т.е экономические величины, которые являются зависимыми и объясняются эконометрической моделью.2. Экзогенные переменные, определяемые вне модели. Они не объясняются моделью и являются внешними, заданными экономическими величинами.3. Лаговые переменные, значения которых отстают на один или несколько периодов. Поскольку лаговые переменные в период времени t также не объясняются эконометрической моделью, то их можно отнести к заранее заданным экзогенным.4. Предопределенные переменные, к которым относятся: а.) обычные экзогенные переменные, они заранее предопределены, так как объясняются фактами, лежащими вне модели;б.) лаговые экзогенные переменные, они заранее предопределены, так как их значения принадлежат предшествующим периодам и объясняются вне модели;в.) лаговые эндогенные переменные, их предопределенность следует из предшествующего объяснения в эконометрической модели.5. Совместно зависимые переменные, которые определяются не одним уравнением, а одновременными уравнениями модели.6. Возмущающие переменные, т.е. экономические величины, не входящие в уравнения эконометрических моделей, но оказывающие влияние на совместно зависимые переменные. Виды эконометрических моделейВ зависимости от цели исследования и поставленных задач эконометрическая модель может быть представлена в различных видах. 1. Структурная форма модели. Она отражает одно- и многосторонние стохастические причинные отношения между экономическими величинами в их непосредственном виде. 2. Полная эконометрическая модель:а.) она охватывает те переменные, которые оказывают существенное влияние на совместно зависимые переменные, а возмущения имеют случайный характер;б.) она содержит столько уравнений, сколько в ней имеется совместно зависимых переменных;в.) система уравнений имеет однозначное решение относительно совместных зависимых переменных. 4. Рекурсивная модель. Модель может быть представлена в следующем виде: В данной системе линейных уравнений зависимая переменная одного уравнения является фактором в других уравнениях. 5. Модель из системы независимых уравнений. В системе каждая эндогенная переменная Эндогенные переменные независимы между собой, структурная и приведенная формы таких моделей совпадают. Оценивание параметров эконометрических моделей Обыкновенный метод наименьших квадратов может применяться для оценивания параметров системы независимых уравнений, рекурсивных и моделей из взаимозависимых переменных.Для решения идентифицируемых уравнений применяется косвенный метод наименьших квадратов. Обычный МНК не учитывает одновременных соотношений между совместно зависимыми переменными, поэтому не может непосредственно применяться.Модель вначале представляется в прогнозной (приведенной) форме. Применяя МНК к каждому полученному уравнению, оценивают все параметры (коэффициенты) системы в прогнозной форме. Так как по предположению все структурные уравнения точно идентифицируемы, на следующем этапе однозначно определяются структурные коэффициенты по коэффициентам прогнозных уравнений. То есть структурные коэффициенты оцениваются косвенно через оценки параметров прогнозной модели.Для решения сверхидентифицированных уравнений применяется двухшаговый метод наименьших квадратов, учитывающий многосторонние связи совместно зависимых переменных. В данном случае структурные уравнения содержат меньше коэффициентов, чем приведенные.Метод является обобщением обычного МНК и выполняется в два этапа. Основная идея двухшагового МНК заключается в замене зависимых переменных Эти расчетные значения эндогенных переменных, находящихся в правой части структурных уравнений, и соответствующие значения экзогенных переменных используются для решения структурных уравнений с помощью МНК.Вновь проверяется надежность полученных решений. Эта проверка необходима, так как при ДМНК решенные структурные уравнения качественно отличны от приведенных уравнений, в том числе имеют другое число степеней свободы вариации, поэтому надежность приведенных уравнений еще не гарантирует надежность решения структурных уравнений.
26. Функциональная - когда каждому значению одной переменной соответствует вполне определенное значение другой. Функциональная зависимость может иметь место как между детерминированными (неслучайными) переменными (например, зависимость скорости падения в вакууме от времени и т.п.), так и между случайными величинами (например, зависимость стоимости проданных изделий от их числа и т.п.).
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.93.168 (0.007 с.) |

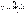 ;общая средняя
;общая средняя  .
. , характеризующий колеблемость групповых
, характеризующий колеблемость групповых , отражающий остаточную, внутригрупповую
, отражающий остаточную, внутригрупповую .При дисперсионном анализе межгрупповую
.При дисперсионном анализе межгрупповую  ивнутригрупповую
ивнутригрупповую  дисперсии определяют путем деления суммы квадратов отклонений на соответствующее число степеней свободы.
дисперсии определяют путем деления суммы квадратов отклонений на соответствующее число степеней свободы. ,где
,где 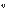 — число единиц в группе:
— число единиц в группе: 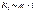 ; т - число групповых средних (число выделенных групп по признаку-фактору);
; т - число групповых средних (число выделенных групп по признаку-фактору);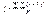 .По таблице F-распределения Р. Фишера (см. приложение 5) при определенном уровне значимости (или доверительной вероятности)1 и числе степеней свободы (К1 и К2) определяется табличное дисперсионное отношение (Fтабл).Если Fрасч >Ftтабл, то следует считать, что гипотеза о влиянии признака-фактора не опровергается. Статистический анализ экономических временных рядов и прогнозирование.Объектом статистического изучения в социальных науках являются сложные системы. Измерение тесноты связей между переменными, построение изолированных уравнений регрессии недостаточны для описания таких систем и объяснения механизма их функционирования. Отдельно взятое уравнение множественной регрессии не может характеризовать истинные влияния отдельных признаков на вариацию результирующей переменной. Именно поэтому в экономических исследованиях важное место заняла проблема описания структуры связей между переменными системой так называемых одновременных уравнений или структурных уравнений.
.По таблице F-распределения Р. Фишера (см. приложение 5) при определенном уровне значимости (или доверительной вероятности)1 и числе степеней свободы (К1 и К2) определяется табличное дисперсионное отношение (Fтабл).Если Fрасч >Ftтабл, то следует считать, что гипотеза о влиянии признака-фактора не опровергается. Статистический анализ экономических временных рядов и прогнозирование.Объектом статистического изучения в социальных науках являются сложные системы. Измерение тесноты связей между переменными, построение изолированных уравнений регрессии недостаточны для описания таких систем и объяснения механизма их функционирования. Отдельно взятое уравнение множественной регрессии не может характеризовать истинные влияния отдельных признаков на вариацию результирующей переменной. Именно поэтому в экономических исследованиях важное место заняла проблема описания структуры связей между переменными системой так называемых одновременных уравнений или структурных уравнений. рассматривается как функция одного и того же набора факторов
рассматривается как функция одного и того же набора факторов  .
. . Благодаря этому содержащиеся в уравнениях переменные приобретают характер предопределенных переменных и применение МНК дает удовлетворительные оценки.Алгоритм метода включает следующие шаги:Структурные уравнения преобразовываются в приведенные.Приведенные уравнения решаются с помощью МНК.Проверяется надежность уравнений по F-критерию.Если уравнения надежны, по ним вычисляются расчетные значения эндогенных переменных для каждой единицы совокупности.
. Благодаря этому содержащиеся в уравнениях переменные приобретают характер предопределенных переменных и применение МНК дает удовлетворительные оценки.Алгоритм метода включает следующие шаги:Структурные уравнения преобразовываются в приведенные.Приведенные уравнения решаются с помощью МНК.Проверяется надежность уравнений по F-критерию.Если уравнения надежны, по ним вычисляются расчетные значения эндогенных переменных для каждой единицы совокупности.


