
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комбинаторика. Элементарная теория вероятностей. Методы вычисления вероятностей.Содержание книги
Поиск на нашем сайте
Предмет теории вероятностей. Пространство элементарных событий. Понятие случайного события. Определения вероятности. Теория вероятностей –математическая наука, изучающая закономерности, присущие массовым случайным явлениям. При этом изучаемые явления рассматриваются в абстрактной форме, независимо от их конкретной природы. То есть теория вероятности рассматривает не сами явления, а их упрощенные схемы-математические модели. 2.Алгебра случайных событий.
Операции над событиями обладают следующими свойствами: А + В = В + А, А *В = В *А- коммутативность, (переместительное); (А + В) + С = А +(В + С), (А*В)*С = А*(В*С)-ассоциативность, (сочетательное); (А + В)С = А*С + В*С-дистрибутивность; А + А = А, А + 1. ∅ Независимые события. Событие А называется независимым от события В, если вероятность события А не зависит от того, наступило событие В или нет. В противном случае событие А называется зависимым от события В. События А и В -независимы. P(A*B)= P(A)* P(B/A)= P(A)* P(B). ТЕОРЕМА: для двух событий верна формула P(A*B)= P(A)* P(B), то события А и В являются независимыми. ЛЕММА: Если событие В не зависит от события А, то событие А не зависит от события В. ЛЕММА: Если события А и В независимы, то независимы и события не А и В, А и не В. ЛЕММА: Если события А и В независимы, то независимы не А и не В. Понятие независимых событий – одно из центральный в теории вероятностей. Понятие независимости может быть распространено на случай n событий. Опр. События А1, А2,…Аn называются независимыми (или независимыми в совокупности), если каждое из них не зависит от произведения любого числа остальных событий и от каждого в отдельности. ТЕОРЕМА: Если события А1, А2,…Аn независимы в совокупности, то вероятность их одновременного появления вычисляется по формуле: P(A1*A2*A3)= P(A1) * P(A2) * P(A3)
Схема Бернулли. Последовательность n-независимых испытаний, в каждой из которых может произойти событие А с вероятностью р, а может произойти не А с вероятностью q, q=1-p=P(A) Формула Бернулли. Если производится n-независимых испытаний в схеме Бернулли, тогда вероятность того, что событие А произойдет n-раз, определяется формулой
Распределение Вейбулла f(x)= {0, x<0 {aλx^a-1*exp(-λx), если x>=0
Математическое ожидание и мода случайной величины, распределённые по закону Вейбула, имеют следующий вид: M(X)=a+bΓ(1+1/n); Распределение Вейбула в ряде случаев характеризует срок службы радиоэлектронной аппаратуры и, кроме того, применяется для аппроксимации различных несимметричных распределений в математической статистике. Распределение Коши
Распределение Парето
Гамма-распределение Говорят, что случайная величина X имеет гамма-распределение с параметрами a>0 и b>0, если её плотность распределения вероятностей имеет вид f(x)= {0, если x<=0 {c*x^λ-1*e^-ax, если x>0 Понятие интервальной оценки При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра. Поэтому при небольшом объеме Статистическая оценка называется интервальной, если она выражается двумя числами – концами интервала Точность оценки. Надежность оценки. Доверительный интервал:Пусть Итак, точностью оценки Надежностью (или доверительной вероятностью) оценки
Так как неравенство доверительным интервалом для оцениваемого параметра В случае "больших" выборок (
Стандартными методами в теории вероятностей устанавливается, что искомая точность оценивания где величина Оценки параметров распределения случайных величин в виде среднего арифметического для оценки математического ожидания и СКО для оценки дисперсии называются точечными оценками, так как они выражаются одним числом. Однако в некоторых случаях знание точечной оценки является недостаточным. Наиболее корректной и наглядной оценкой случайной погрешности измерений является оценка с помощью доверительных интервалов. Симметричный интервал в границами ± Δх(Р) называется доверительным интервалом случайной погрешности с довери-тельной вероятностью Р, если площадь кривой распределения между абсциссами – Δх и + Δх составляет Р -ю часть всей площади под кривой плотности распределения вероятностей. При нормировке всей площади на единицу Р представляет часть этой площади в долях единицы (или в процентах). Другими словами, в интервале от -Dх(Р) до +Dх(Р) с заданной вероятностью Р встречаются Р ×100% всех возможных значений случайной погрешности. Доверительный интервал для нормального распределения находится по формуле:
где коэффициент t зависит от доверительной вероятности Р. Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью: 1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999). Доверительные вероятности для выражения результатов измерений и погрешностей в различных областях науки и техники принимаются равными. Так, в технических измерениях принята доверительная вероятность 0,95. Лишь для особо точных и ответственных измерений принимают более высокие доверительные вероятности. В метрологии используют, как правило, доверитель-ные вероятности 0,97, в исключительных случаях 0,99. Необходимо отметить, что точность измерений должна соответствовать поставленной измерительной задаче. Излишняя точность ведет к неоправданному расходу средств. Недостаточная точность измерений может привести к принятию по его результатам ошибочных решений с самыми непредсказуемыми последствиями, вплоть до серьезных материальных потерь или катастроф. При проведении многократных измерений величины х, подчиняющейся нормальному распределению, доверительный интервал может быть построен для любой доверительной вероятности по формуле:
где tq – коэффициент Стьюдента, зависящий от числа наблюдений n и выбранной доверительной вероятности Р. Он определяется с помощью таблицы q -процентных точек распределения Стьюдента, которая имеет два параметра: k = n – 1 и q = 1 – P; Доверительный интервал для погрешности Dх(Р) позволяет построить доверительный интервал для истинного (действи-тельного) значения измеряемой величины, оценкой которой является среднее арифметическое Недостатком доверительных интервалов при оценке случай-ных погрешностей является то, что при произвольно выбираемых доверительных вероятностях нельзя суммировать несколько погреш-ностей, т.к. доверительный интервал суммы не равен сумме довери-тельных интервалов. Суммируются дисперсии независимых случай-ных величин: Då = åDi. То есть, для возможности суммирования составляющие случайной погрешности должны быть представлены своими СКО, а не предельными или доверительными погрешностя-ми. Цепи Маркова Определение. Цепью Маркова называют последовательность испытаний, в каждом из которых появляется одно и только одно из Например, если последовательность испытаний образует цепь Маркова и полная группа состоит из четырех несовместных событий Заметим, что независимые испытания являются частным случаем цепи Маркова. Действительно, если испытания независимы, то появление некоторого определенного события в любом испытании не зависит от результатов ранее произведенных испытаний. Отсюда следует, что понятие цепи Маркова является обобщением понятия независимых испытаний. Часто при изложении теории цепей Маркова придерживаются иной терминология и говорят о некоторой физической системе Таким образом, события называют состояниями системы, а испытания – изменениями ее состояний. Дадим теперь определение цепи Маркова, используя новую терминологию. Теорема 1. При любых s, t
Доказательство. Вычислим вероятность
Из равенств и следует
Отсюда из равенств (4) и
получим утверждение теоремы. Определим матрицу Так как
Результаты, полученной в теории матриц, позволяют по формуле (6) вычислить
Спектральное разложение Стационарный случайный процесс может быть представлен каноническим разложением вида:
где Vk и Uk –некоррелированные и центрированные случайные величины с дисперсиями D [ Vk ] = D [ Uk ] = Dk; w – неслучайная величина (частота). В этом случае каноническое разложение корреляционной функции определяется выражением
Каноническое разложение называется спектральным разложением стационарного случайного процесса. Спектральное разложение может быть также представлено в виде
где qk – фаза гармонического колебания элементарного стационарного случайного процесса, являющаяся случайной величиной равномерно распределенной в интервале (0, 2 p); Zk – амплитуда гармонического колебания элементарного стационарного случайного процесса – тоже случайная величина. Случайные величины qk и Zk зависимы. Для них имеют место соотношения:
Таким образом, стационарный случайный процесс может быть представлен в виде суммы гармонических колебаний со случайными амплитудами Zk и случайными фазами qk на различных неслучайных частотах wk. Так как корреляционная функция стационарного случайного процесса X (t) является четной функцией своего аргумента, т. е. kx (t) = kx (–t), то ее на интервале (– T, T) можно разложить в ряд Фурье по четным (косинусам) гармоникам
Подставляя в выражение (6.45) t = 0, получим каноническое разложение для дисперсии стационарного случайного процесса:
Таким образом, дисперсия стационарного случайного процесса, представленная своим каноническим разложением, равна сумме дисперсий всех гармоник его спектрального разложения. Используя формулы при k = 1, 2, 3, …, можно построить график изменения дисперсий Dk по частотам wk (рис.6.7). Зависимость Dk = f (wk)в этом случае называется дискретным спектром дисперсий или просто – дискретным спектром стационарного случайного процесса.
Рис.6.7. Дискретный спектр стационарного случайного процесса. В пределе, при В качестве характеристики распределения дисперсии по частотам непрерывного спектра используется спектральная плотность – Sx (w), которую можно рассматривать, как предел отношения дисперсии приходящейся на каждую частоту к D w:
1. Она является неотрицательной функцией частоты:
2. Интеграл от спектральной плотности в пределах от 0 до ∞ равен дисперсии стационарного случайного процесса: Нормированная корреляционная функция и нормированная спектральная плотность также связаны между собой преобразованием Фурье Интеграл от нормированной спектральной плотности в пределах от 0 до ∞ равен единице:
Таблица 6.1 Различные определения спектральной плотности Спектральная плотность
Корреляционная функция
При аналитических расчетах нередко используется спектральная плотность в комплексной форме Спектральная плотность в комплексной форме обладает следующими свойствами: 1.
2. Интеграл от
Пара преобразований Фурье для корреляционной функции и спектральной плотности в комплексной форме имеет вид: Следует отметить, что если спектральную плотность для действительных случайных процессов рассматривать как часть спектральной плотности 19.Основные статистические описания. Вариационный ряд и эмпирические квантили. Распределение частот. Эмпирический коэффициент корреляция. Межгрупповая дисперсия. Ряды распределения, построенные по количественному признаку (возраст, стаж, сроки расследования или рассмотрения дел, число судимостей и т.д.), называются вариационными рядами. Различия единиц совокупности (до 20 лет, 20-24 года, 25-29 лет и т.д.) количественного признака называется вариацией, а сам конкретный признак – вариантой. Вариация признаков может быть дискретной, или прерывной (20, 21, 22, 23, 24, 25 лет и т.д.), либо непрерывной (до 20 лет, 20-25, 25-30 лет и т.д.). При дискретной вариации величина количественного признака (варианты) может принимать вполне определенные значения, отличающиеся в нашем примере на 1 год (20,21,22 и т.д.). При непрерывной вариации величина количественного признака у единиц совокупности в определенном численном промежутке (интервале) может принимать любые значения, хоть сколько-нибудь отличающиеся друг от друга. Например, в интервале 20-25 лет возраст конкретных сотрудников может быть 20 лет и 2 дня, 21 год и 10 месяцев и т.д. Вариационные ряды, построенные по дискретно варьирующим признакам, именуют дискретными вариационными рядами, а построенные по непрерывно варьирующим признакам (интервалам) – интервальными вариационными рядами. Вариационный ряд всегда состоит из двух основных граф (колонок) цифр. В первой колонке указываются значения количественного признака в порядке возрастания. В нашем примере интервального вариационного ряда: до 20 лет, 20-24 года, 25-29 лет и т.д. При дискретной вариации 20, 21, 22, 23, 24, 25 лет. Эти значения количественного признака и называют вариантами. В статистической литературе этот термин иногда употребляется как существительное мужского рода (вариант, варианты), а иногда – как существительное женского рода (варианта, варианты). Во второй колонке указываются числа единиц, которые свойственны той или иной варианте. Их называют частотами, если они выражены в абсолютных числах, т.е. сколько раз в изучаемой совокупности встречается та или иная варианта, или частостями, если они выражены в удельных весах или долях, т.е. в процентах или коэффициентах к итогу. Интервальный вариационный ряд иногда строится с равными интервалами (20-24, 25-29 лет), а иногда с неравными (14-15, 16-18, 19-20, 21-25 лет) интервалами. В первом случае оба интервала равны 5 годам, а во втором случае – 2, 3, 5 годам. При построении интервального ряда с непрерывной вариацией верхняя граница каждого интервала обычно является нижней границей последующего (20-25, 25-30, 30-35 и т.д.), а в построении интервального ряда по дискретному признаку границы смежных интервалов не повторяются (1-5 дней, 6-10 дней, 11-15 дней и т.д.) Статистический анализ вариационных рядов требует не только наличия единичных частот (частостей), но и накопленных частот (частостей). Накопленная частота для той или иной варианты представляет собой сумму частот всех предшествующих вариант (интервалов). В нашем примере (табл. 1) для интервала 20-24 года накопленная частота будет равна: Вариационные ряды легко изображаются графически в виде полигона или гистограммы. Графическое изображение накопленных частот (частостей) воспроизводится в системе прямоугольных координат в виде кумуляты, или кумулятивной кривой. По оси ординат откладывается величина накопленных частот, а по оси абсцисс – возрастающие значения количественного признака. Накопленные частоты и кумулята – это интегральные показатели плотности распределения в вариационном ряду. Квантили и процентные точки распределения.При использовании различных методов математической статистики, особенно разнообразных статистических критериев методов построения интервальных оценок неизвестных параметров широко используются понятия -квантилей и -процентных точек распределения Квантилью уровня q (или -квантилью) непрерывной случайной величины обладающей непрерывной функцией распределения называется такое возможное значение этой случайной величины, для которого вероятность события равна заданной величине q, т. е.
Очевидно, чем больше заданное значение тем больше будет и соответствующая величина квантили Частным случаем квантили — -квантилью является характеристика центра группирования — медиана. Для всякой дискретной случайной величиныфункция распределения с увеличением аргумента меняется, как мы видели, скачтми, и, следовательно, существуют такие значения уровней q, для каждого из которых не найдется возможного значения точно удовлетворяющего уравнению Эмпирическими аналогами теоретических квантилей, как легко понять, будут члены вариационного ряда (порядковые статистики). Из их определения, в частности, следует что порядковая статистика является одновременно выборочной квантилью уровня. Часто вместо понятия квантили используют тесно связанное с ним понятие процентной точки. Под -процентной точкой случайной величины понимается такое ее возможное значение для которого вероятность события равна т. е. Для дискретных случайных величин это определение корректируется аналогично тому, как это делалось при определении квантилей. Из определения квантилей и процентных точек вытекает простое соотношение, их связывающее:
Для ряда наиболее часто встречающихся в статистической практике законов распределения составлены специальные таблицы квантилей и процентных точек. Очевидно, достаточно иметь только одну из таких таблиц, так как если, например, по таблицам процентных точек требуется найти -кванти
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.255.103 (0.016 с.) |

 - {W} всех возможных взаимоисключающих исходов данного опыта называется пространством элементарных событий (коротко: ПЭС), а сами исходыW- элементарными событиями (или «элементами», «точками»).
- {W} всех возможных взаимоисключающих исходов данного опыта называется пространством элементарных событий (коротко: ПЭС), а сами исходыW- элементарными событиями (или «элементами», «точками»). В.
В.
 ,А+∅=А,-поглощение А * А = А, А *
,А+∅=А,-поглощение А * А = А, А *  =А-отрицание отрицание;
=А-отрицание отрицание;  =
=  *
*  , и наоборот-закон де Моргана
, и наоборот-закон де Моргана S 2. из A
S 2. из A 




 выборки следует пользоваться так называемыми интервальными оценками.
выборки следует пользоваться так называемыми интервальными оценками. , покрывающего оцениваемый параметр
, покрывающего оцениваемый параметр  . Уточнение понятия интервальной оценки требует введения ряда важных сопровождающих понятий.
. Уточнение понятия интервальной оценки требует введения ряда важных сопровождающих понятий. – неизвестный оцениваемый параметр теоретического распределения признака Cгенеральной совокупности (
– неизвестный оцениваемый параметр теоретического распределения признака Cгенеральной совокупности ( – его точечная статистическая оценка, найденная по данным выборки (
– его точечная статистическая оценка, найденная по данным выборки ( – случайная величина, меняющаяся от выборки к выборке). Ясно, что оценка
– случайная величина, меняющаяся от выборки к выборке). Ясно, что оценка  тем точнее определяет параметр
тем точнее определяет параметр  . Если рассмотреть неравенство
. Если рассмотреть неравенство  , то число
, то число  будет характеризовать точность оценки (чем меньше
будет характеризовать точность оценки (чем меньше  , тем оценка точнее).
, тем оценка точнее). называется такое положительное число
называется такое положительное число  , которое удовлетворяет неравенству
, которое удовлетворяет неравенству  .Поскольку точечная оценка
.Поскольку точечная оценка  ) удовлетворять неравенству
) удовлетворять неравенству  . Это неравенство является случайным событием и, следовательно, оно может осуществляться лишь с некоторой вероятностью.
. Это неравенство является случайным событием и, следовательно, оно может осуществляться лишь с некоторой вероятностью. , с которой выполняется неравенство
, с которой выполняется неравенство  , т.е.
, т.е. (1)На практике надежность
(1)На практике надежность  назначается (задается наперед): это достаточно большая вероятность (0,95; 0,99; 0,999) – такая, чтобы событие с вероятностью
назначается (задается наперед): это достаточно большая вероятность (0,95; 0,99; 0,999) – такая, чтобы событие с вероятностью  диктуется особенностями каждой конкретно рассматриваемой задачи.
диктуется особенностями каждой конкретно рассматриваемой задачи. равносильно неравенству
равносильно неравенству  , то формулу (1) можно истолковать следующим образом: с заданной надежностью
, то формулу (1) можно истолковать следующим образом: с заданной надежностью  интервал
интервал  накрывает неизвестный оцениваемый параметр
накрывает неизвестный оцениваемый параметр  называется интервал вида
называется интервал вида 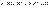 , накрывающий неизвестный параметр
, накрывающий неизвестный параметр  с заданной надежностью
с заданной надежностью  (рис.10.).
(рис.10.). и
и  этого интервала называют доверительными границами.
этого интервала называют доверительными границами. ) стандартными в теории вероятностей методами доказывается, что искомая точность
) стандартными в теории вероятностей методами доказывается, что искомая точность  вычисляется по формуле
вычисляется по формуле , (2)где величина
, (2)где величина  определяется по специальной таблице значений функции Лапласа, исходя из равенства
определяется по специальной таблице значений функции Лапласа, исходя из равенства .Сам же искомый доверительный интервал имеет вид
.Сам же искомый доверительный интервал имеет вид  В случае "малых" выборок (
В случае "малых" выборок ( ) доказывается, что точностьоценивания
) доказывается, что точностьоценивания  находится по формуле
находится по формуле  ,где величина
,где величина  определяется по специальной таблице Стьюдента значений функции
определяется по специальной таблице Стьюдента значений функции  [1].
[1]. вычисляется по формуле
вычисляется по формуле  ,
, определяется по специальной таблице значений функции
определяется по специальной таблице значений функции  [2].
[2].

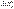 – оценка среднего квадратического отклонения среднего арифметического.
– оценка среднего квадратического отклонения среднего арифметического. . Истинное значение измеряе-мой величины находится с доверительной вероятностью Р внутри интервала:
. Истинное значение измеряе-мой величины находится с доверительной вероятностью Р внутри интервала:  . Доверительный интервал позволяет выяснить, насколько может измениться полученная в результате данной серии измерений оценка измеряемой величины при проведении повторной серии измерений в тех же условиях. Необходимо отметить, что доверительные интервалы строят для неслучайных величин, значения которых неизвестны. Такими являются истинное значение измеряемой величины и средние квадратические отклонения. В то же время оценки этих величин, получаемые в результате обработки данных наблюдений, являются случайными величинами.
. Доверительный интервал позволяет выяснить, насколько может измениться полученная в результате данной серии измерений оценка измеряемой величины при проведении повторной серии измерений в тех же условиях. Необходимо отметить, что доверительные интервалы строят для неслучайных величин, значения которых неизвестны. Такими являются истинное значение измеряемой величины и средние квадратические отклонения. В то же время оценки этих величин, получаемые в результате обработки данных наблюдений, являются случайными величинами. несовместных событий
несовместных событий  полной группы, причем условная вероятность
полной группы, причем условная вероятность  того, что в
того, что в  -м испытании наступит событие
-м испытании наступит событие  , при условии, что в
, при условии, что в  -м испытании наступило событие
-м испытании наступило событие  , не зависит от результатов предшествующих испытаний.
, не зависит от результатов предшествующих испытаний. , причем известно, что в шестом испытании появилось событие
, причем известно, что в шестом испытании появилось событие  , то условная вероятность того, что в седьмом испытании наступит событие
, то условная вероятность того, что в седьмом испытании наступит событие  , не зависит от того, какие события появились в первом, втором, …, пятом испытаниях.
, не зависит от того, какие события появились в первом, втором, …, пятом испытаниях. , которая в каждый момент времени находится в одном из состояний:
, которая в каждый момент времени находится в одном из состояний:  , и меняет свое состояние только в отдельные моменты времени
, и меняет свое состояние только в отдельные моменты времени  то есть система переходит из одного состояния в другое (например из
то есть система переходит из одного состояния в другое (например из  в
в  ). Для цепей Маркова вероятность перейти в какое-либо состояние
). Для цепей Маркова вероятность перейти в какое-либо состояние  в момент
в момент  зависит только от того, в каком состоянии система находилась в момент
зависит только от того, в каком состоянии система находилась в момент  , и не изменяется от того, что становятся известными ее состояния в более ранние моменты. Так же в частности, после испытания система может остаться в том же состоянии («перейти» из состояния
, и не изменяется от того, что становятся известными ее состояния в более ранние моменты. Так же в частности, после испытания система может остаться в том же состоянии («перейти» из состояния  ).
).
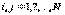 (3)
(3)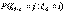 по формуле полной вероятности, положив
по формуле полной вероятности, положив 
 (4)
(4)





 В матричной записи (3) имеет вид
В матричной записи (3) имеет вид  (5)
(5) то
то  где
где  − матрица вероятности перехода. Из (5) следует
− матрица вероятности перехода. Из (5) следует (6)
(6) и исследовать их поведение при
и исследовать их поведение при 

 ,
, ,
, ,
, ,
,  .
.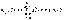 , где wk и Dk определяются выражениями:
, где wk и Dk определяются выражениями: ,
,  , (6.46)
, (6.46)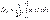 ,
,  .
. .
. (т. е. при
(т. е. при  ) мы перейдем к непрерывному спектру.
) мы перейдем к непрерывному спектру. . В этом случае выражение примет вид:
. В этом случае выражение примет вид: . Таким образом, корреляционная функция и спектральная плотность стационарного случайного процесса связаны косинус-преобразованием Фурье. Следовательно, спектральная плотность стационарного случайного процесса может быть выражена через корреляционную функцию по формуле
. Таким образом, корреляционная функция и спектральная плотность стационарного случайного процесса связаны косинус-преобразованием Фурье. Следовательно, спектральная плотность стационарного случайного процесса может быть выражена через корреляционную функцию по формуле .Спектральная плотность обладает следующими свойствами.
.Спектральная плотность обладает следующими свойствами. . (6.53)
. (6.53) . По аналогии с нормированной корреляционной функцией вводится нормированная спектральная плотность:
. По аналогии с нормированной корреляционной функцией вводится нормированная спектральная плотность:  . (6.55)
. (6.55) ,
, 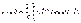 . (6.57)
. (6.57) . Таким образом, если на графике нормированной спектральной плотности (рис.6.8) рассматривать полосу частот от w 1 до w 2, то площадь подграфика, заключенная в интервале от w 1 до w 2, будет равна доле дисперсии случайного процесса, приходящейся на эти частоты. При этом общая площадь подграфика будет равна единице.
. Таким образом, если на графике нормированной спектральной плотности (рис.6.8) рассматривать полосу частот от w 1 до w 2, то площадь подграфика, заключенная в интервале от w 1 до w 2, будет равна доле дисперсии случайного процесса, приходящейся на эти частоты. При этом общая площадь подграфика будет равна единице.







 . В этом случае рассматриваются как положительные, так и отрицательные частоты, а
. В этом случае рассматриваются как положительные, так и отрицательные частоты, а  и S (w) связаны соотношением:
и S (w) связаны соотношением: 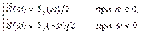
 является неотрицательной функцией частоты, то есть:
является неотрицательной функцией частоты, то есть: .
. в бесконечных пределах равен дисперсии случайного процесса:
в бесконечных пределах равен дисперсии случайного процесса: . 3.
. 3.  .
. ,
,  .
. , лежащую в области положительных частот, то мы получим определение S (w), приведенное в строке 2 таблицы 6.1. Однако в этом случае интеграл от нормированной спектральной плотности будет равен 0.5, а не единице, что с формальной точки зрения не очень хорошо.
, лежащую в области положительных частот, то мы получим определение S (w), приведенное в строке 2 таблицы 6.1. Однако в этом случае интеграл от нормированной спектральной плотности будет равен 0.5, а не единице, что с формальной точки зрения не очень хорошо.





