
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доказательство. По свойству характеристической функцииСодержание книги
Поиск на нашем сайте
Свойство 4. Если Бе́та-распределе́ние в теориивероятностей и статистике — двухпараметрическое семейство абсолютно непрерывных распределений. Используется для описания случайных величин, значения которых ограничены конечным интервалом. Бета распределение. Бета-распределение часто используется для описания процессов, обладающих естественными нижним и верхним пределами. Бета распределения определяется формулой: f(x) = Интервальные статистические оценки. Точные доверительные интервалы. Асимптотические доверительные интервалы. Понятие интервальной оценки При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра. Поэтому при небольшом объеме Статистическая оценка называется интервальной, если она выражается двумя числами – концами интервала Точность оценки. Надежность оценки. Доверительный интервал:Пусть Итак, точностью оценки
Надежностью (или доверительной вероятностью) оценки
Так как неравенство доверительным интервалом для оцениваемого параметра В случае "больших" выборок (
Стандартными методами в теории вероятностей устанавливается, что искомая точность оценивания где величина Оценки параметров распределения случайных величин в виде среднего арифметического для оценки математического ожидания и СКО для оценки дисперсии называются точечными оценками, так как они выражаются одним числом. Однако в некоторых случаях знание точечной оценки является недостаточным. Наиболее корректной и наглядной оценкой случайной погрешности измерений является оценка с помощью доверительных интервалов. Симметричный интервал в границами ± Δх(Р) называется доверительным интервалом случайной погрешности с довери-тельной вероятностью Р, если площадь кривой распределения между абсциссами – Δх и + Δх составляет Р -ю часть всей площади под кривой плотности распределения вероятностей. При нормировке всей площади на единицу Р представляет часть этой площади в долях единицы (или в процентах). Другими словами, в интервале от -Dх(Р) до +Dх(Р) с заданной вероятностью Р встречаются Р ×100% всех возможных значений случайной погрешности.
Доверительный интервал для нормального распределения находится по формуле:
где коэффициент t зависит от доверительной вероятности Р. Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью: 1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999). Доверительные вероятности для выражения результатов измерений и погрешностей в различных областях науки и техники принимаются равными. Так, в технических измерениях принята доверительная вероятность 0,95. Лишь для особо точных и ответственных измерений принимают более высокие доверительные вероятности. В метрологии используют, как правило, доверитель-ные вероятности 0,97, в исключительных случаях 0,99. Необходимо отметить, что точность измерений должна соответствовать поставленной измерительной задаче. Излишняя точность ведет к неоправданному расходу средств. Недостаточная точность измерений может привести к принятию по его результатам ошибочных решений с самыми непредсказуемыми последствиями, вплоть до серьезных материальных потерь или катастроф. При проведении многократных измерений величины х, подчиняющейся нормальному распределению, доверительный интервал может быть построен для любой доверительной вероятности по формуле:
где tq – коэффициент Стьюдента, зависящий от числа наблюдений n и выбранной доверительной вероятности Р. Он определяется с помощью таблицы q -процентных точек распределения Стьюдента, которая имеет два параметра: k = n – 1 и q = 1 – P; Доверительный интервал для погрешности Dх(Р) позволяет построить доверительный интервал для истинного (действи-тельного) значения измеряемой величины, оценкой которой является среднее арифметическое Недостатком доверительных интервалов при оценке случай-ных погрешностей является то, что при произвольно выбираемых доверительных вероятностях нельзя суммировать несколько погреш-ностей, т.к. доверительный интервал суммы не равен сумме довери-тельных интервалов. Суммируются дисперсии независимых случай-ных величин: Då = åDi. То есть, для возможности суммирования составляющие случайной погрешности должны быть представлены своими СКО, а не предельными или доверительными погрешностя-ми.
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.175.68 (0.011 с.) |

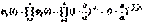 - что есть характеристическая функция случайной величины, распределенной по
- что есть характеристическая функция случайной величины, распределенной по  .
. независимы и имеют стандартное нормальное распределение, то
независимы и имеют стандартное нормальное распределение, то  Доказательство. Вытекает из свойств 2 и 3.
Доказательство. Вытекает из свойств 2 и 3. (
( +
+  )/(
)/( (
( (
( )) * x
)) * x  -1 * (1-x)
-1 * (1-x)  -1 0
-1 0  x
x  1
1 выборки следует пользоваться так называемыми интервальными оценками.
выборки следует пользоваться так называемыми интервальными оценками. , покрывающего оцениваемый параметр
, покрывающего оцениваемый параметр  . Уточнение понятия интервальной оценки требует введения ряда важных сопровождающих понятий.
. Уточнение понятия интервальной оценки требует введения ряда важных сопровождающих понятий. – неизвестный оцениваемый параметр теоретического распределения признака Cгенеральной совокупности (
– неизвестный оцениваемый параметр теоретического распределения признака Cгенеральной совокупности ( – его точечная статистическая оценка, найденная по данным выборки (
– его точечная статистическая оценка, найденная по данным выборки ( – случайная величина, меняющаяся от выборки к выборке). Ясно, что оценка
– случайная величина, меняющаяся от выборки к выборке). Ясно, что оценка  тем точнее определяет параметр
тем точнее определяет параметр  . Если рассмотреть неравенство
. Если рассмотреть неравенство  , то число
, то число  будет характеризовать точность оценки (чем меньше
будет характеризовать точность оценки (чем меньше  , тем оценка точнее).
, тем оценка точнее). называется такое положительное число
называется такое положительное число  , которое удовлетворяет неравенству
, которое удовлетворяет неравенству  .Поскольку точечная оценка
.Поскольку точечная оценка  ) удовлетворять неравенству
) удовлетворять неравенству  . Это неравенство является случайным событием и, следовательно, оно может осуществляться лишь с некоторой вероятностью.
. Это неравенство является случайным событием и, следовательно, оно может осуществляться лишь с некоторой вероятностью. , с которой выполняется неравенство
, с которой выполняется неравенство  , т.е.
, т.е. (1)На практике надежность
(1)На практике надежность  назначается (задается наперед): это достаточно большая вероятность (0,95; 0,99; 0,999) – такая, чтобы событие с вероятностью
назначается (задается наперед): это достаточно большая вероятность (0,95; 0,99; 0,999) – такая, чтобы событие с вероятностью  диктуется особенностями каждой конкретно рассматриваемой задачи.
диктуется особенностями каждой конкретно рассматриваемой задачи. равносильно неравенству
равносильно неравенству  , то формулу (1) можно истолковать следующим образом: с заданной надежностью
, то формулу (1) можно истолковать следующим образом: с заданной надежностью  интервал
интервал  накрывает неизвестный оцениваемый параметр
накрывает неизвестный оцениваемый параметр  называется интервал вида
называется интервал вида 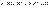 , накрывающий неизвестный параметр
, накрывающий неизвестный параметр  с заданной надежностью
с заданной надежностью  (рис.10.).
(рис.10.). и
и  этого интервала называют доверительными границами.
этого интервала называют доверительными границами. ) стандартными в теории вероятностей методами доказывается, что искомая точность
) стандартными в теории вероятностей методами доказывается, что искомая точность  вычисляется по формуле
вычисляется по формуле , (2)где величина
, (2)где величина  определяется по специальной таблице значений функции Лапласа, исходя из равенства
определяется по специальной таблице значений функции Лапласа, исходя из равенства .Сам же искомый доверительный интервал имеет вид
.Сам же искомый доверительный интервал имеет вид  В случае "малых" выборок (
В случае "малых" выборок ( ) доказывается, что точностьоценивания
) доказывается, что точностьоценивания  находится по формуле
находится по формуле  ,где величина
,где величина  определяется по специальной таблице Стьюдента значений функции
определяется по специальной таблице Стьюдента значений функции  [1].
[1]. вычисляется по формуле
вычисляется по формуле  ,
, определяется по специальной таблице значений функции
определяется по специальной таблице значений функции  [2].
[2].

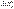 – оценка среднего квадратического отклонения среднего арифметического.
– оценка среднего квадратического отклонения среднего арифметического. . Истинное значение измеряе-мой величины находится с доверительной вероятностью Р внутри интервала:
. Истинное значение измеряе-мой величины находится с доверительной вероятностью Р внутри интервала:  . Доверительный интервал позволяет выяснить, насколько может измениться полученная в результате данной серии измерений оценка измеряемой величины при проведении повторной серии измерений в тех же условиях. Необходимо отметить, что доверительные интервалы строят для неслучайных величин, значения которых неизвестны. Такими являются истинное значение измеряемой величины и средние квадратические отклонения. В то же время оценки этих величин, получаемые в результате обработки данных наблюдений, являются случайными величинами.
. Доверительный интервал позволяет выяснить, насколько может измениться полученная в результате данной серии измерений оценка измеряемой величины при проведении повторной серии измерений в тех же условиях. Необходимо отметить, что доверительные интервалы строят для неслучайных величин, значения которых неизвестны. Такими являются истинное значение измеряемой величины и средние квадратические отклонения. В то же время оценки этих величин, получаемые в результате обработки данных наблюдений, являются случайными величинами.


