
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретная случайная величина. Типичные законы распределения дискретной величины.Содержание книги
Поиск на нашем сайте Случайная величина- величина в результате опытов принимает то или иное значение, причем заранее не известно какое именно. Дискретная- случайная величина, принимающие конечное или счетное множество значений. Непрерывная - случайная величина, принимающие несчетные множество значений. Для задания дискретной случайной величины недостаточно перечислить все ее возможные значения, нужно указать еще и их вероятность. Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления. Закон распределения можно задать таблично, аналитически (в виде формулы) или графически (в виде многоугольника распределения). Рассмотрим случайную величину X, которая принимает значения x1, x2, x3... xn с некоторой вероятностью pi, где i = 1.. n. Сумма вероятностей pi равна 1.
Таблица соответствия значений случайной величины и их вероятностей вида
называется рядом распределения дискретной случайной величины или просто рядом распределения. Эта таблица является наиболее удобной формой задания дискретной случайной величины. Графическое представление этой таблицы называется многоугольником распределения. По оси абсцисс откладываются возможные значения дискретной случайной величины, а по оси ординат соответствующие вероятности.
Пуассоновский поток событий. Пуассоновский поток – это поток обладающий двумя свойствами – ординарностью и отсутствием последействия. Для двух неперекрывающихся интервалов времени число событий, попадающих в один интервал, не зависит от того, сколько событий попало в другой. Пусть дан стационарный поток с интенсивностью - вероятность наступления одного события за время - вероятность ненаступления события Функции распределения случайной величины и ее свойства Фун-ия распред. случ. величины Х- называется функ-ей F(x), кот. для любого числа Х из множества R равна вероятности событий Св-ва: 1) F(x)- неубывающая фун-ия, т.е. x2>x1; F(x1)≥F(x2) 2) F(x)- ограниченная 0≤F(x)≤1 3) 4) 5) F(x;y) непрерывная слева фун-ия Вероятность попадания случ. величины Х в промежуток от А до В принимающие ее фун-ии распределения на промежуток [a;b] P{a≤x≤b}=F(b)-F(a) дискретная случайная величина, принимающая значения xесли x 1 < x 2 < … < xi < … с вероятностями p 1 < p 2 < … < pi < …, то таблица вида
называется распределением дискретной случайной величины.Функция распределения случайной величины, с таким распределением, имеет вид У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:
Плотностью распределения вероятностей непрерывной случайной величины Х называется производная ее функции распределения f(x)=F’(x) Св-ва 1) f(x) неотрицательная, т.е. f(x)≥0 2) Вероятность попадания н.с.в. в промежуток [a;b) равна определенному интегралу от ее плотности в пределах от a до b, т.е. 3) Функция распределения н.с.в. может быть выражена через ее плотность вероятности по формуле 4) Условие нормировки: несобственный интеграл от плотности вероятности н.с.в в бесконечных пределах равен единице, т.е. Числа, назначение которых в сжатом виде характеризовать основные особенности распределений случайных величин, называются числовыми характеристиками. Рассмотрим некоторые из числовых характеристик и их основные свойства.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

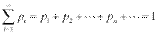

 . Из ординарности потока следует:
. Из ординарности потока следует: :
: 






 .
.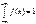 Закон распределения случайной величины дает исчерпывающую информацию о случайной величине. Однако, иногда можно охарактеризовать достаточно ярко случайную величину с помощью всего одного или нескольких чисел. Например, можно указать закон распределения количества осадков выпадающих в данной местности за определенный месяц, но проще инагляднее указать среднее количество осадков в данном месяце.
Закон распределения случайной величины дает исчерпывающую информацию о случайной величине. Однако, иногда можно охарактеризовать достаточно ярко случайную величину с помощью всего одного или нескольких чисел. Например, можно указать закон распределения количества осадков выпадающих в данной местности за определенный месяц, но проще инагляднее указать среднее количество осадков в данном месяце.


