
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следствие. Пусть X1, . . .Xn; Y1, . . . ,Yn – значения признаков X и Y в выборочной совокупности объема n, Cov(X ,Y )– ковариация признаков X и Y в генеральной совокупностиСодержание книги
Поиск на нашем сайте
объема N. Тогда для ковариации выборочных средних справедливы соотношения: • в случае повторной выборки Cov(X¯,Y¯) =Cov(X,Y)/n • в случае бесповторной выборки Cov(¯X, ¯Y) =Cov(X,Y)/n ·N –n/N −1 Выборочная доля (w), или частость, определяется отношением числа единиц, обладающих изучаемым признаком т, к общему числу единиц выборочной совокупности п: w= т/п. Например, если из 100 деталей выборки (и = 100), 95 деталей оказались стандартными (т =95), то выборочная доля w = 95 / 100 = 0,95. Пропорциональная (Типическая, районированная, стратифицированная) выборка преследует две цели: • обеспечить представительство в выборке соответствующих типических групп генеральной совокупности по интересующим исследователя признакам; • увеличить точность результатов выборочного обследования. При типической выборке до начала ее формирования генеральная совокупность единиц разбивается на типические группы. При этом очень важным моментом является правильный выбор группировочного признака. Выделенные типические группы могут содержать одинаковое или различное число единиц отбора. В первом случае выборочная совокупность формируется с одинаковой долей отбора из каждой группы, во втором – с долей, пропорциональной ее доле в генеральной совокупности. Если выборка формируется с равной долей отбора, по существу она равносильна ряду собственно случайных выборок из меньших генеральных совокупностей, каждая из которых и есть типическая группа. Отбор из каждой группы осуществляется в случайном (повторном или бесповторном) либо механическом порядке. При типической выборке, как с равной, так и неравной долей отбора, удается устранить влияние межгрупповой вариации изучаемого признака на точность ее результатов, так как обеспечивается обязательное представительство в выборочной совокупности каждой из типических групп. Стандартная ошибка выборки будет зависеть не от величины общей дисперсии,а от величины средней из групповых дисперсий. Поскольку средняя из групповых дисперсий всегда меньше общей дисперсии, постольку при прочих равных условиях стандартная ошибка типической выборки будет меньше стандартной ошибки собственно случайной выборки. При определении стандартных ошибок типической выборки применяются следующие формулы: • при повторном способе отбора
8.Пределные теоремы в схеме Бернулли. Приближенные формулы Лапласа. Теорема Пуассона. К настоящему моменту мы накопили значительное число точных результатов, относящихся к последовательности независимых испытаний Бернулли и связанному с ней биномиальному распределению. Мы знаем, что Vn, число успехов в последовательности из Vn=ɛ1+...+ɛn где ɛ1+...+ɛn - независимые одинаково распределенные бернуллиевские случайные величины. Мы знаем в явном виде распределение, Vn,а именно,
где p - вероятность успеха в единичном испытании. Вместе с тем, во многих задачах приходится находить вероятности Локальная приближенная формула Лапласа. При больших n имеет место приближенное равенство
где (Таблицу значений функции j(х) см. в приложении 1). Локальная теорема Лапласа Если вероятность р наступления события А постоянно отлично от 0 и 1, а число испытаний достаточно велико, то вероятность может быть вычисленно по следующей формуле
Замечание1: равенство тем точнее, чем >n Определение: Замечание2: Интегральная приближенная формула Лапласа. При больших n имеет место приближенное равенство
где
Функция Ф (х) называется функцией Лапласа (таблицу ее значений см. в приложении). При нахождении значений функции j(х) и Ф (х) для отрицательных значений аргументов следует иметь в виду, что j(х) четная, а Ф (х) – нечетная. Отметим еще, что приближенными формулами Лапласа (1) и (2) на практике пользуются в случае, если npq ³ 10. Если же npq < 10, то эти формулы приводят к довольно большим погрешностям. Интегральная теорема Лапласа. Если вероятность наступления р события А постоянно отлично от 0 и 1, то тгда вероятность того, что событие А состоится m-раз в промежутке от k1 до k2 равна Р(А)=р, р
Теорема Пуассона. Если число испытаний неограниченно увеличивается (n→∞) и вероятность наступления события А неограниченно уменьшается, но так что произведение числа испытаний (np=λ=const) на вероятность события является постоянной, тогда вероятность удовлетворить предельному равенству
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.216.248 (0.006 с.) |

 • при бесповторном способе отбора:
• при бесповторном способе отбора:  средняя из групповых дисперсий в выборочной совокупности.
средняя из групповых дисперсий в выборочной совокупности. независимых испытаний Бернулли, можно представить в виде
независимых испытаний Бернулли, можно представить в виде
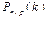 при больших значениях n. Это может вызвать значительные вычислительные трудности ввиду громоздкости биномиальных коэффициентов
при больших значениях n. Это может вызвать значительные вычислительные трудности ввиду громоздкости биномиальных коэффициентов  и необходимости возводить числа
и необходимости возводить числа  и
и  в высокие степени. Ниже мы рассмотрим две важные предельные ситуации, когда биномиальное распределение может быть приближено другими распределениями.
в высокие степени. Ниже мы рассмотрим две важные предельные ситуации, когда биномиальное распределение может быть приближено другими распределениями. , (1)
, (1) ,
,  .
.
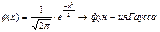

 , (2)
, (2)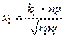 ,
,  ,
, 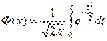 .
. 0 и р
0 и р 





