
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точечные оценки параметров распределения. Методы моментов, максимального правдоподобия, наименьших квадратов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Оценка параметра называется точечной, если она выражается одним числом. Задача нахождения точечных оценок – частный случай статистической задачи нахождения оценок параметров функции распределения случайной величины на основании выборки. Любая точечная оценка, вычисленная на основании опытных данных, является их функцией и поэтому сама должна представлять собой случайную величину с распределением, зависящим от распределения исходной случайной величины, в том числе от самого оцениваемого параметра и от числа опытов n. Точечные оценки могут быть состоятельными, несмещенными и эффективными. Состоятельной называется оценка, которая при увеличении объема выборки стремится по вероятности к истинному значению числовой характеристики. Несмещенной называется оценка, математическое ожидание которой равно оцениваемой числовой характеристике (параметру).Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра, т.е. наиболее эффективной считают ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию. Требование несмещенности на практике не всегда целесообразно, так как оценка с небольшим смещением и малой дисперсией может оказаться предпочтительнее несмещенной оценки с большой дисперсией. На практике не всегда удается удовлетворить одновременно все три этих требования, однако выбору оценки должен предшествовать ее критический анализ со всех перечисленных точек зрения.Наиболее распространенным методом получения оценок является, метод наибольшего (максимального) правдоподобия, теоретически обоснованный математиком Р. Фишером, который приводит к асимптотически несмещенным и эффективным оценкам с приближенно нормальным распределением. Среди других методов можно назвать методы моментов и наименьших квадратов.Точечной оценкой математического ожидания результата измерений является среднее арифметическое значение измеряемой величины При любом законе распределения оно является состоятельной и несмещенной оценкой, а также наиболее эффективной по критерию наименьших квадратов. Точечная оценка дисперсии, определяемая по формуле, является несмещенной и состоятельной. Ме́тод моме́нтов — метод оценки неизвестных параметров распределений в математической статистике и эконометрике, основанный на предполагаемых свойствах моментов (Пирсон, 1894 г.). Идея метода заключается в замене истинных соотношений выборочными аналогами. Суть метода: Пусть случайная величина (вектор, матрица и т. д.) X имеет некоторое распределение
Пусть
причем в данном представлении (когда справа от равенства — ноль) достаточно использовать просто суммы вместо средних. Оценки, получаемые из решения этой системы уравнений (выборочных условий на моменты), называются оценками метода моментов. Название метода связано с тем, что чаще всего в качестве функций Если моментные функции непрерывны, то оценки метода моментов состоятельны. Преимущества и недостатки метода: В известной мере, при оценке параметров из известного семейства вероятностных распределений, этот метод упраздняется Фишеровским методом максимального правдоподобия, так как максимально правдоподобная оценка имеет большую вероятность оказаться ближе к истинному значению оцениваемой величины. Тем не менее, в некоторых случаях, например, как выше в случае гамма-распределения, использование метода максимального правдоподобия требует использования компьютеров, в то время как метод моментов может быть быстро и легко реализован вручную. Оценки, полученные методом моментов, могут быть использованы как первое приближение для метода максимума правдоподобия. Дальнейшее улучшение оценок может быть получено с использованием метода Ньютона-Рафсона. В некоторых случаях, редких при больших объемах данных и более частых при малом их количестве, оценки, даваемые методом моментов могут оказаться вне допустимой области. Такая проблема никогда не возникает в методе максимального правдоподобия. Также, оценки по методу моментов не обязательно оказываются достаточной статистикой, то есть, они иногда извлекают из данных не всю имеющуюся в них информацию. Ме́тод максима́льного правдоподо́бия или метод наибольшего правдоподобия (ММП, ML, MLE — англ. maximum likelihood estimation) в математической статистике — это метод оценивания неизвестного параметра путём максимизации функции правдоподобия[1]. Основан на предположении о том, что вся информация о статистической выборке содержится в функции правдоподобия. Метод максимального правдоподобия был проанализирован, рекомендован и значительно популяризирован Р. Фишером между 1912 и 1922 годами (хотя ранее он был использован Гауссом,Лапласом и другими).Оценка максимального правдоподобия является популярным статистическим методом, который используется для создания статистической модели на основе данных, и обеспечения оценки параметров модели. Метод максимального правдоподобия соответствует многим известным методам оценки в области статистики. Например, вы интересуетесь таким антропометрическим параметром, как рост жителей России. Предположим, у вас имеются данные о росте некоторого количества людей, а не всего населения. Кроме того предполагается, что рост является нормально распределённойвеличиной с неизвестной дисперсией и средним значением. Среднее значение и дисперсия роста в выборке являются максимально правдоподобными к среднему значению и дисперсии всего населения. Для фиксированного набора данных и базовой вероятностной модели, используя метод максимального правдоподобия, мы получим значения параметров модели, которые делают данные «более близкими» к реальным. Оценка максимального правдоподобия даёт уникальный и простой способ определить решения в случае нормального распределения. Метод оценки максимального правдоподобия применяется для широкого круга статистических моделей, в том числе: линейные модели и обобщённые линейные модели;факторный анализ;моделирование структурных уравнений;многие ситуации, в рамках проверки гипотезы и доверительного интервала формирования;дискретные модели выбора. Метод максимального правдоподобия, сокращенно ММП (термин был впервые использован в работе Фишера, 1922) - это общий метод оценивания параметров генеральной совокупности с помощью максимизации функции правдоподобия L выборки. Функция правдоподобия L есть совместное распределение выборки, которое представляет собой функцию параметра
Если выборка имеет непрерывное распределение, функция правдоподобия L описывается совместной плотностью распределения В случае, если элементы выборки Величину Пусть L - функция правдоподобия выборки; при наблюдаемых значениях - является функцией параметров θ.
Тогда оценками максимального правдоподобия θ называются наиболее правдоподобные значения
Очевидно, оценки зависят от наблюдений Часто проще искать точку максимума функции Пусть Метод наименьших квадратов является одним из наиболее распространенных и наиболее разработанных вследствие своей простоты и эффективности методов оценки параметров линейных эконометрических моделей. Вместе с тем, при его применении следует соблюдать определенную осторожность, поскольку построенные с его использованием модели могут не удовлетворять целому ряду требований к качеству их параметров и, вследствие этого, недостаточно “хорошо” отображать закономерности развития процесса Рассмотрим процедуру оценки параметров линейной эконометрической модели с помощью метода наименьших квадратов более подробно. Такая модель в общем виде может быть представлена уравнением (1.2): yt = a0 + a1 х1t +...+ an хnt + εt. Исходными данными при оценке параметров a0 , a1 ,..., an является вектор значений зависимой переменной y = (y1, y2,..., yT)' и матрица значений независимых переменных
в которой первый столбец, состоящий из единиц, соответствует коэффициенту модели Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной.
22. Основные распределения в статистике. Квантилии и процентные точки распределения. Распределения хи-квадрат (закон Пирсона), Стьюента, Фишера, гамма-распределение, бета-распределение. Ряд распределния является одним из видов группировок. Ряд распределения — представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку.В зависимости от признака, положенного в основу образования ряда распределения различают атрибутивные и вариационные ряды распределения: -Атрибутивными — называют ряды распределения, построенные по качественными признакам. -Ряды распределения, построенные в порядке возрастания или убывания значений количественного признака называются вариационными. Вариационный ряд распределения состоит из двух столбцов:В первом столбце приводятся количественные значения варьирующегося признака, которые называются вариантами и обозначаются Частоты — это абсолютные числа, показывающие столько раз в совокупности встречается данное значение признака, которые обозначают
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 835; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.195.15 (0.01 с.) |



 , зависящее от параметров
, зависящее от параметров  . Пусть для функций (называемых моментами или моментными функциями)
. Пусть для функций (называемых моментами или моментными функциями)  , интегрируемых по мере
, интегрируемых по мере  , выполнены условия на моменты
, выполнены условия на моменты
 — выборка случайной величины X. Предполагается, что соотношения аналогичные условиям на моменты выполнены и для выборки, а именно вместо математического ожидания в условиях на моменты необходимо использовать выборочные средние:
— выборка случайной величины X. Предполагается, что соотношения аналогичные условиям на моменты выполнены и для выборки, а именно вместо математического ожидания в условиях на моменты необходимо использовать выборочные средние:
 выступают функции степенного вида, математические ожидания от которых в теории вероятностей и математической статистике принято называть моментами.
выступают функции степенного вида, математические ожидания от которых в теории вероятностей и математической статистике принято называть моментами. .
. - вектор неизвестных параметров модели
- вектор неизвестных параметров модели
 имеют дискретное распределение, функция правдоподобия принимает вид
имеют дискретное распределение, функция правдоподобия принимает вид 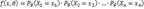
 можно считать мерой правдоподобия значения θ при заданной реализации x.
можно считать мерой правдоподобия значения θ при заданной реализации x.
 максимизирующие функцию L.
максимизирующие функцию L.
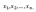 В широких предположениях эти оценки являются оптимальными.
В широких предположениях эти оценки являются оптимальными. , которая совпадает с
, которая совпадает с  в силу монотонности логарифма.
в силу монотонности логарифма. - это элемент пространства
- это элемент пространства  Если
Если  открытый интервал, а
открытый интервал, а  дифференцируема и достигает максимума на
дифференцируема и достигает максимума на  то оценки максимального правдоподобия удовлетворяют уравнению
то оценки максимального правдоподобия удовлетворяют уравнению 
 .
.
 .
. . Дискретная варианта — выражается целым числом. Интервальная варианта находится в пределах от и до. В зависимости от типа варианты можно построить дискретный или интервальный вариационный ряд.
. Дискретная варианта — выражается целым числом. Интервальная варианта находится в пределах от и до. В зависимости от типа варианты можно построить дискретный или интервальный вариационный ряд. . Сумма всех частот равна должна быть равна численности единиц всей совокупности. Частости (
. Сумма всех частот равна должна быть равна численности единиц всей совокупности. Частости ( ) — это частоты выраженные в процентах к итогу. Сумма всех частостей выраженных в процентах должна быть равна 100% в долях единице.
) — это частоты выраженные в процентах к итогу. Сумма всех частостей выраженных в процентах должна быть равна 100% в долях единице.


