
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эффективность точечной оценки.Содержание книги
Поиск на нашем сайте
Опр. Несмещенная оценка Замечания: 1) В отличие от несмещенности и состоятельности, эффективность зависит от закона распределения 2) Для проверки эффективности можно использовать неравенство Крамера-Рао:
Если 46. Метод максимального правдоподобия. Пусть снова Выборочный вектор – вектор (Х1,Х2…Хn), где Хi одинаково распределены и независимы (х1,х2…хn) – реализация выборочного вектора. Функция правдоподобия выборки: - для непрерывного генерального – плотность распределения выборочного вектора, взятая в точке его реализации; - для дискретного генерального – вероятность реализации данного выборочного вектора. Обозначение
Оценками максимального правдоподобия (ММП-оценками) называются такие значения параметров ( Обозначим ММП-оценку вектора
Метод моментов. Пусть з-н распределения интервальной совокупности Х известен с точностью до параметров
Получим систему m уравнений, для нахождения оценок:
Пример. Пусть
Найти ММ оценки параметров а и b: Находим:
Общее: и для 47 и 48: Пусть неизвестная функция генеральной совокупности зависит от некоторого параметра Примеры статистик. Эта оценка Будет рассматриваться, как приближенное значение параметра
Качество оценки устанавливают, проверяя, выполняются ли следующие три свойства (требования).Требования, предъявляемые к точечным оценкам: 1. Несмещенность, т.е. Это свойство желательно, но не обязательно. Часто полученная оценка бывает существенной, но ее можно поправить так, что она станет несмещенной. Иногда оценка бывает смещенной, но асимптотически несмещенной, т.е. 2. Состоятельность, т.е. Это свойство является обязательным. Несостоятельные оценки не используются. 3. Эффективность. а) Если оценки Если б) Если оценки Если Где Рассмотрим использование этих свойств на примерах выбора оценок МО и дисперсии:
48. Выборочная дисперсия Докажем, что выборочная дисперсия является смещенной оценкой для дисперсии генеральной совокупности. Выполним следующие преобразования
Найдем МО для дисперсии:
МО не совпадает с s 2, а отличается на –s2/n – смещение. Таким образом эта оценка занимает в среднем истинное значение дисперсии на величину s2/n, правда это смещение сходит на нет при n ® ¥. Чтобы устранить это смещение надо «исправить» дисперсию.
Можно доказать, что статистика S2 является и состоятельной оценкой для дисперсии генеральной совокупности. Замечание. К сожалению, на практике при оценке параметров не всегда оказывается возможным одновременное выполнение требований: несмещенности, эффективности и состоятельности.
49. Выборочное среднее: а) Несмещенность. По определению выборочного вектора
M[Xсред]=M[(1/n)åXi]=(1/n)M[åXi]= (1/n)åM[Xi]=(1/n)nm D[Xсред]=D[(1/n)åXi]=(1/n2)D[åXi]= (1/n2)åD[Xi]=(1/n)ns2=s2/n б) Состоятельность Воспользуемся неравенством Чебышева: Применим это неравенство к При n ®¥
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.93.10 (0.008 с.) |

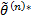 параметра
параметра  называется эффективной, если её дисперсия минимальна по сравнению со всеми возможными оценками
называется эффективной, если её дисперсия минимальна по сравнению со всеми возможными оценками 
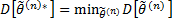

 , где
, где 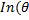 ) – информация Фишера
) – информация Фишера
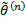 – эффективна.
– эффективна.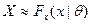 . Требуется оценить векторный параметр
. Требуется оценить векторный параметр 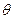 .
.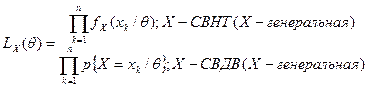
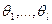 ), которые доставляют максимум функции правдоподобия выборки.
), которые доставляют максимум функции правдоподобия выборки. . Пусть
. Пусть 
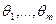 . Выберем m каких-либо начальных и центральных моментов
. Выберем m каких-либо начальных и центральных моментов 
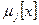 , найдем теоретически их зависимость от
, найдем теоретически их зависимость от 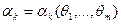
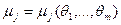 и приравняем эти зависимости к соответствующим выборочным моментам
и приравняем эти зависимости к соответствующим выборочным моментам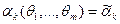

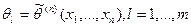
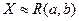 (равномерное распределение)
(равномерное распределение)
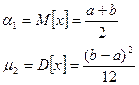


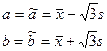
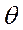 . Нужно по наблюдениям оценить параметр. Для построения оценок используются статистики – функции от выборочных значений.
. Нужно по наблюдениям оценить параметр. Для построения оценок используются статистики – функции от выборочных значений.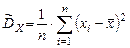 .
.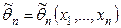 .
.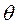 . Замечание. Как правило, для оценки параметра
. Замечание. Как правило, для оценки параметра 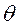 можно использовать несколько статистик, получая при этом различные значения параметра
можно использовать несколько статистик, получая при этом различные значения параметра 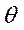 . Как измерить «близость» оценки
. Как измерить «близость» оценки  к истинному значению
к истинному значению 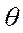 ? Как определить качество оценки? Комментарий: Качество оценки определяется не по одной конкретной выборке, а по всему мыслимому набору конкретных выборок, т.е. по случайному выборочному вектору
? Как определить качество оценки? Комментарий: Качество оценки определяется не по одной конкретной выборке, а по всему мыслимому набору конкретных выборок, т.е. по случайному выборочному вектору  , поэтому для установления качества полученных оценок моментов
, поэтому для установления качества полученных оценок моментов 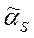 ,
, 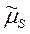 следует во всех этих формулах заменить конкретные выборочные значения
следует во всех этих формулах заменить конкретные выборочные значения 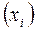 на СВ Xi.
на СВ Xi. ;
; 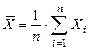 ;
;  .
.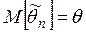 .
.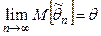 .
.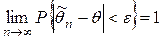 .
.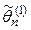 и
и 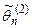 – несмещенные, то
– несмещенные, то 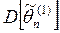 и
и  .
.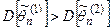 , то оценка
, то оценка 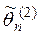 более эффективна, чем
более эффективна, чем 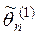 .
.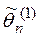 и
и  – смещенные, тогда
– смещенные, тогда 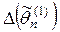 и
и 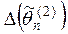 .
. , то оценка
, то оценка 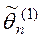 .
.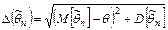 – средний квадрат отклонения оценки.
– средний квадрат отклонения оценки.
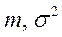
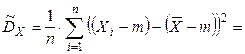
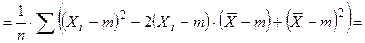
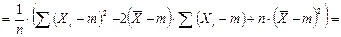
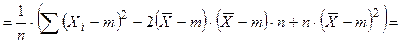
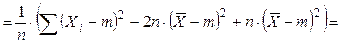
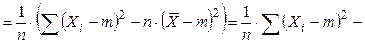
 ;
; 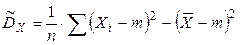 .
.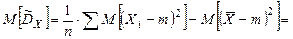
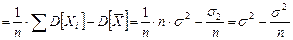 .
. .
. ;
; 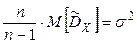
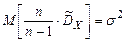 ;
; 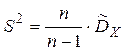
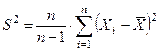 .
. является несмещенной и состоятельной оценкой МО генеральной совокупности (X1 ,…, Xn), причем каждое Xi совпадает с m и s 2.
является несмещенной и состоятельной оценкой МО генеральной совокупности (X1 ,…, Xn), причем каждое Xi совпадает с m и s 2.
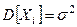 , причем Xi – независимые в совокупности СВ, тогда вычислим
, причем Xi – независимые в совокупности СВ, тогда вычислим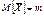 g.
g.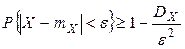
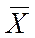
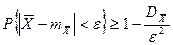

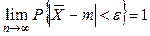 ,что и доказывает состоятельность
,что и доказывает состоятельность 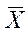 .
.


