
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет теории вероятностей.Содержание книги
Поиск на нашем сайте Предмет теории вероятностей. Используется 2 основных типа моделей: 1) Детерминированная: При повторении заданного опыта в неизменных условиях, событие А происходит всякий раз. П1. Опыт: К проводнику сопротивлением R приложено напряжение U. А={течет ток I=U/R}. 2) Вероятностная: При повторении опыта в неизменных условиях событие А может произойти или нет. Такие события и опыт называют случайными. П2. Подбрасывают монету. A={Выпадет «герб»}. ТВ изучает случайные события и их числовые характеристики. Статистическая вероятность. Еще в древности заметили статистическую устойчивость случайных явлений: если случайный опыт повторяется многократно, то отношение числа mn(A) появлений события А к числу n опытов приближается к некоторому числу P*(A). mn(A)/n= P*(A), n – велико. P*(A) – статистическая вероятность. Используется при составлении частотных словарей, разработке клавиатуры и т.д.
№2 Случайные события и связанные с ними понятия. Алгебраические операции над событиями. Случайные события. Случайный опыт – это создание заданного комплекса условий и наблюдение результата. Результат интерпретируется как случайное событие(исход). Пространство элементарных исходов – мн-во простейших(неразложимых в рамках данного опыта на более простые) взаимоисключающих исходов Случайное событие – любое подмн-во Основные понятия связанные со случайными событиями: 1) Всё пр-во элементарных исходов в 2) Пустое множество Ǿ 3) Суммой событий А и В называется событие А+В состоящее из элем исходов входящих в мн-во 4) Произведение А и В это событие сост. из элементарных исходов входящих в мн-во 5) Разность событий А и В – событие состоящее из элементарных исходов, входящих в мн-во А\В. Т.о. событие А произошло, а В нет. 6) Событие А влечет за собой В, если А – подмножество В( 7) Событие 8) События А и В называются несовместными если нет Св-ва: 1)Коммутативность: А+В=В+А; АВ=ВА. 2)Ассоциативность: (А+В)+С=А+(В+С); (АВ)С=А(ВС). 3)Дистрибутивность: (А+В)С=АС+ВС; А+ВС=(А+В)(А+С).
№3 Классическое определение вероятности. События равновероятные, если нет объективных оснований для того, чтобы, одно из них было более или менее вероятным чем другое. Случайный опыт удовлетворяющий условиям: а) б) все элем. исходы равновозможны называется классической схемой. Пусть Р(А)= Св-ва: 1)Р(А)>0 2) 3)Если А и В несовместны, (АВ= Ǿ), то Р(А+В)=Р(А)+Р(В).
№4 Геометрические вероятности Пусть случайный опыт состоит в случайном выборе точки на прямой R1 или плоскости R2 или n мерного пространства Rn. На прямой рассмотрим только мн-ва Длина, площадь, объем – мера множества Пусть случайная точка Пусть П1. 2 судна должны подойти к причалу для разгрузки в течении суток. Одновременная разгрузка невозможна. Разгрузка любого из них длится 8 часов. С какиой вероятностью одно будет ожидать разгрузки другого? х- время прихода однеого
 у – время прихода другого у – время прихода другого
(х,у)
A = {(х,у) mes( P(A)=5/9 Cв-ва: 1)Р(А) 2) 3)А и В несовместимы.
№5 Понятие об аксиоматической вероятности Пусть Чтобы вместе с вероятностью событий А и Если П1. А={ из 4х карточек 1,2,3 и 4 случайно выбирают одну} Найдем F: Ǿ
Пусть 1) Р(А) 2) 3) Для
1) 2) В П1 Р
№6 Св-ва вероятности Из основных св-в вероятности: 1) Р(А) 2) 3)АВ= Ǿ => Р(А+В)=Р(А)+Р(В) Вытекают другие св-ва: 4) 5) Р(Ǿ)=0 6) 7) 8)Р(А+В)=Р(А)+Р(В)-Р(АВ) №7 Условная вероятность и ее свойства. Теорема умножения. Пусть в случайном опыте Т могут появиться события А и В. Если известно что В произошло то говорят об условной вероятности события А при условии В Р(А/В). В произошло => реализуется один из N(B) элементарных исходов
Опр. Пусть (
Замеч. 1)Аналогично, если 2) Теорема умножения Вер-ть произведения 1. 2. 3.
4)Усл вер-ть обладает всеми св-ми дрю вер-тей. 5) Усл. Вер-ть P(A/B) можно рассм.,как обычную вероятность, определенную на новом про-ве Эл. Исходов 6) Для n событий формула:
№8 Независимые события, их свойства. Независимость в совокупности. Опр. А независимое событие от В, если P(A/B)=P(A) Свойства: 1) Свойство независимости взаимно, т.е. P(B/A)=P(B)
Т.е. А и В взаимно независимы. 2) Если А и В независимы, то P(AB)=P(A)*P(B) верно и обратное: Опр. События А1,A2,A3,…,An независимы в совокупности, если любое из них не зависит от каждого из остальных n от всех возможных произведений этих остальных. Опр. События A1,A2,…,An независимы в совокупности если: P(A1,A2,…,An)=P(A1)*P(A2)…P(An) Замечание Для независимости в совокупности недостаточно попарной независимости. №9 Формула полной вероятности. Пусть события H1,…,Hn могут произойти в случайном опыте Т. Эти события образуют полную группу событий, если H1+H2+…+Hn= Если к тому же события {Hz} попарно несовместимы (Hi,Hj Теорема. Пусть в случ опыте могут произойти события А,H1,..,Hn, причем {Hi} образуют полную группу несовместимых событий, то A=A* P(A)=P(AH1)+P(AH2)+…+P(AHn)=> теоре. Умножения P(A)=P(H1)P(A/H1)+…+P(Hn)P(A/Hn)
№10 Формула Байеса Теорема В условиях предыдущей теоремы
P(Hk/A)=(P(Hk)P(A/Hk))/P(A) По теореме умножения P(A)*P(Hk/A)=P(A*Hk)=P(Hk)P(A/Hk) /: P(A) P(Hk/A)=(P(Hk)P(A/Hk)/P(A))
№11 Схема Бернулли Повторные испытания – это проведение n раз одного и тогоже случ опыта или проведение одновременное n одинаковых опытов. Схема Бернулли – это случ опыт состоящий в n повторных испытаниях, причем 1) z исхода (А-успех, (не)А – неудача) 2) испытания независимы, т.е. P(A) не зависит от исходов в др. испытыниях 3) p и q=1-p не изм от пыта к опыту Найдем вер-ть pn,m появления ровно m раз успеха в серии из т испытаний. В силу независимости испытаний вер-ть каждого такого исхода равно
Случайные велечины Случайная величина = это числовая переменная, принимающая свои значения в зависимости от исхода некоторого случайного опыта Опр. Пусть ( Опр. Функцией распределения (Вер-тей) случ величины x наз функция: Fx(x)=P{X<x} Св - ва Fx(x) 1 P{a<=x<b}=Fx(b)-Fx(a) Пусть есть события {x<b},{x<a},{a<=x<=b} {x<b}={x<a}+{a<=x<=b}
2 P{a<=x<=b}=Fx(b+0)-Fx(a) 3 P{a<x<b}= Fx(b)-Fx(a+0) 4 P{a<x<=b}=Fx(b+0)-Fx(a) 5 P{x=a} = Fx(a+0)-Fx(a) Другие свойства 1 Fx(x) не убыв функция 2 0<=Fx(x)<=1 3 Fx(- 4 Fx(x) в t точках a
№13 Дискретная случайная величина Опр Случайная величина X, мн-во значений которой конечно или счетно называеться случайной величиной дискретного типа (СВДТ) Закон распределения СВДТ описываеться с помощью Fx, но удобнее представлять в виде ряда распределений
Очевидно что сумма =1 Св-ва Fx(x) СВДТ: а) кусочно постоянная б) Fx(x)=0 при x<x1 в) в точка xi терпит разрыв 1-го рода
№14 Биноминальное распределение
Дискретная X имеет бин распределение с параметрами n, p(X~B(n,p)), если X принимает 0,1,…,n с Вер-мя p(n,k)= P{X=k}= Очевидно B(n,p) описывает случ число успехов в серии n испытаний по схеме Бернулли с вер-тью успеха p. Опр. Пусть X-CВДТ с рядом расп-й причем числовой ряд Для бин распр-я: X= P q p
M[x]= Дисперсия B(n,p): D[X]=
№15 Распределение Пуассона Теорема Пуассона Пусть n->бесконечность и p->0 так что np=
З-и Pn( Мат ожидание:
Дисперсия: Dx=
Непр. Случайная. Величина. Опр. X наз-ся непр, если Fx(x)=P{X<x}= Св-ва fx(x): 1 P{a<=X<b}= 2 для любого a принадлежащего ГR P{X=a}=0 3 fx(x)>=0 4 5 В точках непр-ти: fx(x)=F’x(x)
№17 Нормальный закон распределения
Непр случайная величина X распределена по нормальному з-ну распр-я с параметрами m,t(X~N(m,t)) если ее функция плотности имеет вид Распределение N(0,1) называеться стандартизированным нормальным: Ф(x)= Благодаря св-ву Ф(-x)=(-Ф(x)), x>=0 в таблицу можно приводить значения Ф(x) только для x>=0 Математическое ожидание M[x]= Дисперсия D[x]= Найдем для x~N(m, P{a<x<b}= В частном случае P{/X-m/<l}=2Ф(l/ Метод моментов. Пусть з-н распределения интервальной совокупности Х известен с точностью до параметров
Получим систему m уравнений, для нахождения оценок:
Пример. Пусть
Найти ММ оценки параметров а и b: Находим:
Общее: и для 47 и 48: Пусть неизвестная функция генеральной совокупности зависит от некоторого параметра Примеры статистик. Эта оценка Будет рассматриваться, как приближенное значение параметра
Качество оценки устанавливают, проверяя, выполняются ли следующие три свойства (требования).Требования, предъявляемые к точечным оценкам: 1. Несмещенность, т.е. Это свойство желательно, но не обязательно. Часто полученная оценка бывает существенной, но ее можно поправить так, что она станет несмещенной. Иногда оценка бывает смещенной, но асимптотически несмещенной, т.е. 2. Состоятельность, т.е. Это свойство является обязательным. Несостоятельные оценки не используются. 3. Эффективность. а) Если оценки Если б) Если оценки Если Где Рассмотрим использование этих свойств на примерах выбора оценок МО и дисперсии:
48. Выборочная дисперсия Докажем, что выборочная дисперсия является смещенной оценкой для дисперсии генеральной совокупности. Выполним следующие преобразования
Найдем МО для дисперсии:
МО не совпадает с s 2, а отличается на –s2/n – смещение. Таким образом эта оценка занимает в среднем истинное значение дисперсии на величину s2/n, правда это смещение сходит на нет при n ® ¥. Чтобы устранить это смещение надо «исправить» дисперсию.
Можно доказать, что статистика S2 является и состоятельной оценкой для дисперсии генеральной совокупности. Замечание. К сожалению, на практике при оценке параметров не всегда оказывается возможным одновременное выполнение требований: несмещенности, эффективности и состоятельности.
49. Выборочное среднее: а) Несмещенность. По определению выборочного вектора
M[Xсред]=M[(1/n)åXi]=(1/n)M[åXi]= (1/n)åM[Xi]=(1/n)nm D[Xсред]=D[(1/n)åXi]=(1/n2)D[åXi]= (1/n2)åD[Xi]=(1/n)ns2=s2/n б) Состоятельность Воспользуемся неравенством Чебышева: Применим это неравенство к При n ®¥
Ошибки 1 и 2 рода Статистическое решение может быть ошибочным. При этом различают ошибки I-го и II-го родов. Опр. Ошибкой первого рода называется ошибка, состоящая в том, что гипотеза Н0 отклоняется, когда Н0 – верна. Вероятность P{ZÎVkïH0}=a.. Опр Ошибкой второго рода называется ошибка, состоящая в том, что принимается гипотеза Н0, но в действительности верна альтернативная гипотеза Н1. Вероятность ошибки второго рода при условии, что гипотеза Н1 – простая, P{ZÎV\VkïH1}=b. Проверка статистических гипотез и доверительных интервалов.Проверка гипотез с использованием критерия значимости может быть проведена на основе доверительных интервалов. При этом одностороннему критерию значимости будет соответствовать односторонний доверительный интервал, а двустороннему критерию значимости будет соответствовать, двусторонний доверительный интервал. Гипотеза Н0 – принимается, если значение q0 накрывается доверительным интервалом, иначе отклоняется.
57. Критерий Критерий Процедура применения критерия Этапы: 1. По выборке найти оценки неизвестных параметров предполагаемого закона 2. Если Х–СВДТ – определить частоты Если Х–СВНТ – разбить множество значений на r – непересекающихся интервалов 3. Х–СВДТ вычислить Х–СВНТ вычислить
4. 5. Принять статистическое решение.
e – количество оцениваемых параметров. Малочисленные частоты надо будет объединять. Проверка гипотезы о равномерном распределении генеральной совокупности. n = 200 А;
1.
2.
k = 10 – 2 – 1 = 7
Предмет теории вероятностей. Используется 2 основных типа моделей: 1) Детерминированная: При повторении заданного опыта в неизменных условиях, событие А происходит всякий раз. П1. Опыт: К проводнику сопротивлением R приложено напряжение U. А={течет ток I=U/R}. 2) Вероятностная: При повторении опыта в неизменных условиях событие А может произойти или нет. Такие события и опыт называют случайными. П2. Подбрасывают монету. A={Выпадет «герб»}. ТВ изучает случайные события и их числовые характеристики. Статистическая вероятность. Еще в древности заметили статистическую устойчивость случайных явлений: если случайный опыт повторяется многократно, то отношение числа mn(A) появлений события А к числу n опытов приближается к некоторому числу P*(A). mn(A)/n= P*(A), n – велико. P*(A) – статистическая вероятность. Используется при составлении частотных словарей, разработке клавиатуры и т.д.
№2 Случайные события и связанные с ними понятия. Алгебраические операции над событиями. Случайные события. Случайный опыт – это создание заданного комплекса условий и наблюдение результата. Результат интерпретируется как случайное событие(исход). Пространство элементарных исходов – мн-во простейших(неразложимых в рамках данного опыта на более простые) взаимоисключающих исходов Случайное событие – любое подмн-во Основные понятия связанные со случайными событиями: 1) Всё пр-во элементарных исходов в 2) Пустое множество Ǿ 3) Суммой событий А и В называется событие А+В состоящее из элем исходов входящих в мн-во 4) Произведение А и В это событие сост. из элементарных исходов входящих в мн-во 5) Разность событий А и В – событие состоящее из элементарных исходов, входящих в мн-во А\В. Т.о. событие А произошло, а В нет. 6) Событие А влечет за собой В, если А – подмножество В( 7) Событие 8) События А и В называются несовместными если нет Св-ва: 1)Коммутативность: А+В=В+А; АВ=ВА. 2)Ассоциативность: (А+В)+С=А+(В+С); (АВ)С=А(ВС). 3)Дистрибутивность: (А+В)С=АС+ВС; А+ВС=(А+В)(А+С).
№3 Классическое определение вероятности. События равновероятные, если нет объективных оснований для того, чтобы, одно из них было более или менее вероятным чем другое. Случайный опыт удовлетворяющий условиям: а) б) все элем. исходы равновозможны называется классической схемой. Пусть Р(А)= Св-ва: 1)Р(А)>0 2) 3)Если А и В несовместны, (АВ= Ǿ), то Р(А+В)=Р(А)+Р(В).
№4 Геометрические вероятности Пусть случайный опыт состоит в случайном выборе точки на прямой R1 или плоскости R2 или n мерного пространства Rn. На прямой рассмотрим только мн-ва Длина, площадь, объем – мера множества Пусть случайная точка Пусть П1. 2 судна должны подойти к причалу для разгрузки в течении суток. Одновременная разгрузка невозможна. Разгрузка любого из них длится 8 часов. С какиой вероятностью одно будет ожидать разгрузки другого? х- время прихода однеого
 у – время прихода другого у – время прихода другого
(х,у)
A = {(х,у) mes( P(A)=5/9 Cв-ва: 1)Р(А) 2) 3)А и В несовместимы.
№5 Понятие об аксиом |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

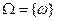 так, что опыт всегда заканчивается появлением одного и только одного элементарного исхода
так, что опыт всегда заканчивается появлением одного и только одного элементарного исхода  .
. пр-ва элем. исходов заданного случайного опыта. Если результат опыта
пр-ва элем. исходов заданного случайного опыта. Если результат опыта 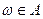 , то событие А произошло.
, то событие А произошло.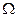 называется достоверным событием. Очевидно достоверное событие происходит в любом опыте.
называется достоверным событием. Очевидно достоверное событие происходит в любом опыте.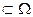 называется невозможным событием. Очевидно невозможное событие не происходит в опыте.
называется невозможным событием. Очевидно невозможное событие не происходит в опыте.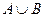 . Т.о. событие А+В состоит в том что произошло хотябы одно из событий А и В.
. Т.о. событие А+В состоит в том что произошло хотябы одно из событий А и В.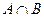 . Т.о. произведение А и В состоит в том что А и В произошли одновременно.
. Т.о. произведение А и В состоит в том что А и В произошли одновременно.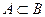 ). Т.о. всякий раз, когда происходит А, происходит и В.
). Т.о. всякий раз, когда происходит А, происходит и В.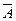 состоит из
состоит из  , не входящих в А, называется противоположным А
, не входящих в А, называется противоположным А классическая схема,
классическая схема, 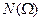 -число элементарных исходов,
-число элементарных исходов,  - число исходов благоприятствующих событию А. Тогда вероятность события А:
- число исходов благоприятствующих событию А. Тогда вероятность события А:
 в R2
в R2 |
| 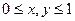 }
}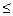 1/3}
1/3}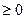

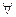 событию А, связанному со случайным опытом
событию А, связанному со случайным опытом 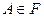 .
.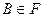 можно было найти А+В, АВ, А-В,
можно было найти А+В, АВ, А-В,  ,
, 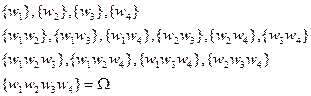
 (аксиома неотрицательности)
(аксиома неотрицательности)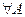 и В
и В  , таких что АВ= Ǿ. Р(А+В)=Р(А)+Р(В) (аксиома сложения)
, таких что АВ= Ǿ. Р(А+В)=Р(А)+Р(В) (аксиома сложения)
 - вероятность элементарного исхода
- вероятность элементарного исхода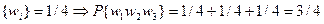
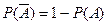

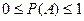
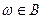 . Из N(AB) исходов
. Из N(AB) исходов 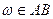 благоприятствуют A
благоприятствуют A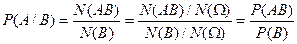
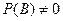 , тогда усл.вероятностью А наз-тся число:
, тогда усл.вероятностью А наз-тся число: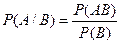
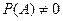 :
: 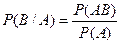
 событий равна вер-ти одного из них и умноженной на усл.вер-ть другой.
событий равна вер-ти одного из них и умноженной на усл.вер-ть другой.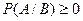
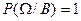
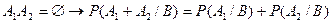
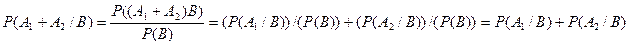
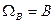
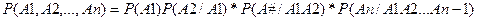
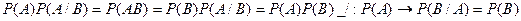
 0, i
0, i 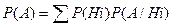
 Число таких элементарных исходов
Число таких элементарных исходов  Потому:
Потому:
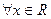 ) мн-во
) мн-во  } принадлежит алгебре событий F.Полную инф-ю о случ величине ч содержит ее закон расп-я, позволяющий найти Верн-ть для
} принадлежит алгебре событий F.Полную инф-ю о случ величине ч содержит ее закон расп-я, позволяющий найти Верн-ть для 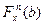

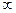 )=0, Fx(+
)=0, Fx(+  ГR непр слева
ГR непр слева Fx(x)=P{X<x}=
Fx(x)=P{X<x}= 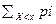

 сх-ся, тогда m=M[x]=
сх-ся, тогда m=M[x]= 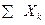 , где Xk 0 1
, где Xk 0 1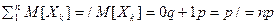
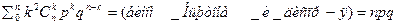
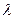 =const, тогда
=const, тогда 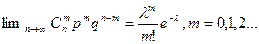
 Случайная величина X со знач 0,1,2,…,k и вер-ми pk=p{X=k}=
Случайная величина X со знач 0,1,2,…,k и вер-ми pk=p{X=k}= 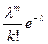 ,
, 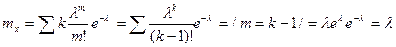
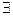 неотриц функция Fx(x)(функция плотности расп-я), так что:
неотриц функция Fx(x)(функция плотности расп-я), так что: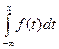
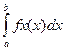
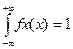 (условие нормировки
(условие нормировки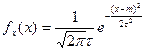
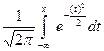 -функция Лапласа
-функция Лапласа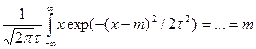 -> M[x]=m
-> M[x]=m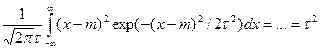
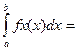
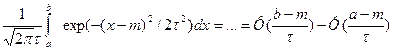
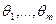 . Выберем m каких-либо начальных и центральных моментов
. Выберем m каких-либо начальных и центральных моментов 
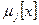 , найдем теоретически их зависимость от
, найдем теоретически их зависимость от 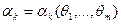
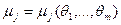 и приравняем эти зависимости к соответствующим выборочным моментам
и приравняем эти зависимости к соответствующим выборочным моментам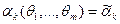

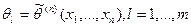
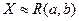 (равномерное распределение)
(равномерное распределение)
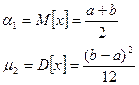


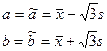
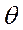 . Нужно по наблюдениям оценить параметр. Для построения оценок используются статистики – функции от выборочных значений.
. Нужно по наблюдениям оценить параметр. Для построения оценок используются статистики – функции от выборочных значений.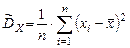 .
.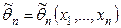 .
.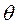 . Замечание. Как правило, для оценки параметра
. Замечание. Как правило, для оценки параметра 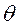 можно использовать несколько статистик, получая при этом различные значения параметра
можно использовать несколько статистик, получая при этом различные значения параметра 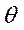 . Как измерить «близость» оценки
. Как измерить «близость» оценки  к истинному значению
к истинному значению 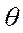 ? Как определить качество оценки? Комментарий: Качество оценки определяется не по одной конкретной выборке, а по всему мыслимому набору конкретных выборок, т.е. по случайному выборочному вектору
? Как определить качество оценки? Комментарий: Качество оценки определяется не по одной конкретной выборке, а по всему мыслимому набору конкретных выборок, т.е. по случайному выборочному вектору  , поэтому для установления качества полученных оценок моментов
, поэтому для установления качества полученных оценок моментов 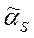 ,
, 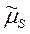 следует во всех этих формулах заменить конкретные выборочные значения
следует во всех этих формулах заменить конкретные выборочные значения 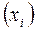 на СВ Xi.
на СВ Xi. ;
; 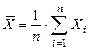 ;
;  .
.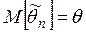 .
.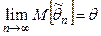 .
.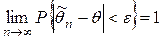 .
.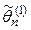 и
и 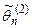 – несмещенные, то
– несмещенные, то 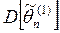 и
и  .
.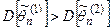 , то оценка
, то оценка 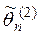 более эффективна, чем
более эффективна, чем 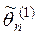 .
.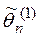 и
и  – смещенные, тогда
– смещенные, тогда 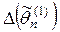 и
и 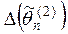 .
. , то оценка
, то оценка 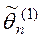 .
.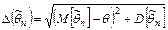 – средний квадрат отклонения оценки.
– средний квадрат отклонения оценки.
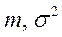
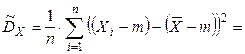
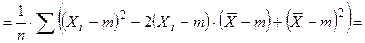
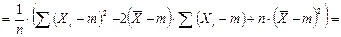
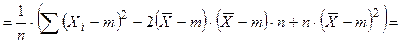
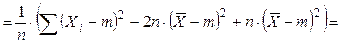
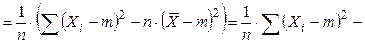
 ;
; 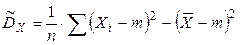 .
.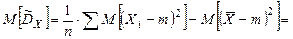
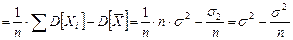 .
. .
. ;
; 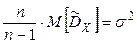
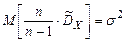 ;
; 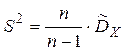
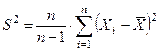 .
. является несмещенной и состоятельной оценкой МО генеральной совокупности (X1 ,…, Xn), причем каждое Xi совпадает с m и s 2.
является несмещенной и состоятельной оценкой МО генеральной совокупности (X1 ,…, Xn), причем каждое Xi совпадает с m и s 2.
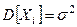 , причем Xi – независимые в совокупности СВ, тогда вычислим
, причем Xi – независимые в совокупности СВ, тогда вычислим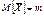 g.
g.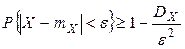
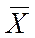
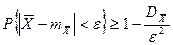

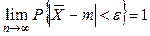 ,что и доказывает состоятельность
,что и доказывает состоятельность 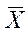 .
.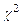 и его применение.
и его применение.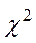 применяется в частности для проверки гипотез о виде распределения генеральной совокупности.
применяется в частности для проверки гипотез о виде распределения генеральной совокупности. для проверки гипотезы H0, утверждающей, что СВ Х имеет закон распределения
для проверки гипотезы H0, утверждающей, что СВ Х имеет закон распределения 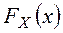 состоит из следующих этапов.
состоит из следующих этапов. .
.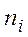 , i = 1, 2, …, r, с которым каждое значение встречается в выборке.
, i = 1, 2, …, r, с которым каждое значение встречается в выборке. и попавших в каждый из этих интервалов
и попавших в каждый из этих интервалов  .
. .
. .
.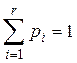
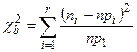 .
.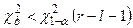 – гипотеза Н0 – принимается.
– гипотеза Н0 – принимается.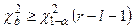 – гипотеза Н0 – отклоняется.
– гипотеза Н0 – отклоняется.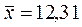
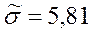
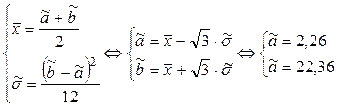
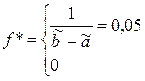
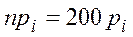
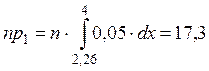

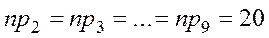

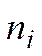
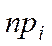

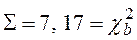
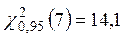
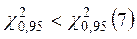 – нет основания отвергать гипотезу о том, что выборка взята из генеральной совокупности и имеет равномерное распределение.
– нет основания отвергать гипотезу о том, что выборка взята из генеральной совокупности и имеет равномерное распределение.


