
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристическая функция случайной величины, её свойства.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Биномиальное распределение в теории вероятностей — распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна p.
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона играет ключевую роль в Теории массового обслуживания.
Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний
№28 Композиционая устойчивость Опр.: Пусть X1 и Х2 распределены по одному и тому же закону (возможно с разными параметрами) и независимы. Если при этом Х1+Х2 распределена по тому же закону, то говорят, что данный закон композиционно устойчив. П1: • Т.е. при фиксированном значении p з-н B(n,p) композиционно устойчив. П2: • П3: •
№31 Ковариация двух случайных величин: Опр: Ковариацией Х и Y называется число (если сov[X,Y] = M[(X-M[X])(Y-M[Y])]= M[Ẋ,Ẏ]. Св-ва: 1) сov[X,Y] = сov[Y,X] 2) сov[X,X] = D[X] 3) сov[X,Y1+Y2] = сov[X,Y1] + сov[X,Y2] 4) сov[C*X,Y]= C* сov[X,Y] 5) D[X+Y]=D[X] + D[Y] + 2 сov[X,Y] 6) |сov[X,Y]| ≤ • 0≤ D[tX+Y] = t^2*D[X] + D[Y] + 2t*cov[X,Y]
№32 Коэффициент корреляциии. Опр: Коэффициентом корреляции называется число:
Св-ва: 1) 2) Если X и Y независимы => •cov[X,Y]=M[XY] – M[X]M[Y] = |тк Х и Y независимы|= M[X]M[Y] – M[X]M[Y] =0 => 3) Если Y=aX+b, то • Пусть M[X] = m, D[X]= cov[X,Y] = M[(X-m)(ax+b – (am+b))] = a* M[(X-m)^2] =
Замеч: Если X и Y независимы, то №33 Распределения Опр: Пусть Xi – независимые случайные величины, Св-ва: 1) M[Y]=n; D[Y]=2n 2) Рисуем графики (оси: f
Опр: Пусть случ. величины 1) Рисуем графики (оси: St 2) При
Опр: Пусть Св-во: Пусть Fn1,n2,p – квантиль распределения F(n1,n2) порядка p, тогда Fn1,n2,(1-p) = 1/ Fn1,n2,p
№34 Неравенства Чебышева Теорема 1 (1ое неравенство Чебышева): Пусть Х – случайная величина, • Рассмотрим случайную величину Очевидно,
Теорема 2 (2ое неравенство Чебышева): Пусть Х-случайная величина, • Рассмотрим непр. Х:
№35 Закон больших чисел(теорема Маркова): Теорема Маркова: Пусть последовательность случ величин •Обозначим
№36 Следствия из закона больших чисел 1) Теорема Чебышева Пусть 2) Пусть
3) Пусть •
№37 Центральная предельная теорема Опр: Пусть Теорема: Пусть последовательность 1) 2) 3) Тогда для Замечания: 1)При достаточно больших n - 2) Условие (2) не является принципиальным. Если
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 546; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |







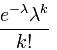
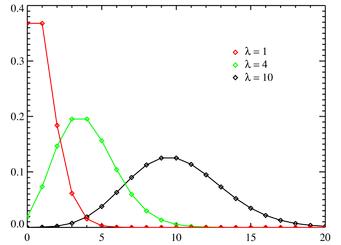


 ,
,  и Х1,Х2 независимы
и Х1,Х2 независимы ,
,  . Т.к. Х1 и Х2 независимы:
. Т.к. Х1 и Х2 независимы:  =>
=>  •
• ,
, 
 ,
,  . Т.к. Х1 и Х2 независимы:
. Т.к. Х1 и Х2 независимы:  =>
=>  •
• ,
,  и Х1,Х2 независимы
и Х1,Х2 независимы ,
, 
 =>
=>  •
• ):
):
 = 4 (сov[X,Y])^2 – 4* D[X]*D[Y] => |сov[X,Y]| ≤
= 4 (сov[X,Y])^2 – 4* D[X]*D[Y] => |сov[X,Y]| ≤ 

 (обратное неверно)
(обратное неверно) •
•
 тогда M[Y] = am+b, D[Y]=
тогда M[Y] = am+b, D[Y]= 

 •
• используется в качестве меры линейной зависимости Х и Y. Если
используется в качестве меры линейной зависимости Х и Y. Если  – зависимость слабая. Если
– зависимость слабая. Если  - зависимость сильная. Если
- зависимость сильная. Если 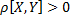 - то при росте одной случайной величины, другая в среднем растет.
- то при росте одной случайной величины, другая в среднем растет.
 . Тогда случайная величина
. Тогда случайная величина  имеет распределение
имеет распределение  («хи-квадрат») с n степенями свободы -
(«хи-квадрат») с n степенями свободы - 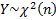
 и
и  с n степенями свободы.
с n степенями свободы.  .
. (x) и ось «х»)...n1>n2 - n2 более пологий и лежит ниже n1
(x) и ось «х»)...n1>n2 - n2 более пологий и лежит ниже n1 St(0,1) приближается к N(0,1)
St(0,1) приближается к N(0,1) и
и  - независимые случайные величины. Тогда
- независимые случайные величины. Тогда  распределена по закону Фишера со степенями свободы n1 и n2
распределена по закону Фишера со степенями свободы n1 и n2 . Тогда
. Тогда 

 или
или  ;
; •
• ,
,  . Тогда
. Тогда 
 •
• сходится по вероятности к числу a (
сходится по вероятности к числу a ( ), если
), если  (или
(или  )
)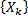 удовлетворяет условиям:
удовлетворяет условиям:  и
и  . Тогда
. Тогда  , т.е.
, т.е.  .
. ,
,  ,
,  . Применяем второе неравенство Чебышева:
. Применяем второе неравенство Чебышева: •
•
 ,
,  . Тогда
. Тогда  или
или 
 , т.е
, т.е  - число успехов в серии n испытаний в схеме Бернулли с вероятностью успеха p. Тогда
- число успехов в серии n испытаний в схеме Бернулли с вероятностью успеха p. Тогда  , т.е
, т.е 


 по следствию (2)•
по следствию (2)• - последовательность случайных величин. Говорят, что случайная величина
- последовательность случайных величин. Говорят, что случайная величина  имеет асимптотическое нормальное распределение с параметрами
имеет асимптотическое нормальное распределение с параметрами  при
при 
 .
.  - функция Лапласа. Обозн:
- функция Лапласа. Обозн:  .
. ,
, 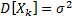
 справедливо
справедливо  .
. , т.е. сумма большого числа одинаково распределенных независимых случайных величин имеет распределение, близкое к нормальному.
, т.е. сумма большого числа одинаково распределенных независимых случайных величин имеет распределение, близкое к нормальному. ,
,  , то при некоторых требованиях вместо условия (3) при больших n имеем:
, то при некоторых требованиях вместо условия (3) при больших n имеем: , т.е. и в этом случае сумма достаточно большого числа случайных величин распределена приблизительно нормально.
, т.е. и в этом случае сумма достаточно большого числа случайных величин распределена приблизительно нормально.


