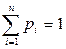Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретные и непрерывные случайные величиныСодержание книги
Поиск на нашем сайте Случайные величины
Математическое ожидание ДСВ и его свойства
Пусть дана случайная величина Х:
Опр. Математическое ожидание дискретной случайной величины X равно сумме произведений значений случайной величины на соответствующие им вероятности:
Предположим, что подбрасывают монету. Если выпадет герб, выигрывают одно очко, если цифра, — проигрывают одно очко. Чему равен ожидаемый выигрыш? Интуитивно понятно, что шансы выиграть и проиграть одну и ту же сумму очков равны, и, следовательно, в среднем ожидаемый выигрыш будет равен нулю, Выигрыш в этой игре — случайная величина; можно вычислить ожидаемое значение, используя формулу (1):
М(Х)= 1 • 1/2 + (-1) • 1/2 = 0. Поэтому математическое ожидание называют средним значением. Причина такого названия состоит в том, что среднее значение случайной величины есть оценка, которую ожидают получить.
Свойства математического ожидания ДСВ 1. Математическое ожидание постоянной величины равно этой постоянной: М(С) = С. 2. Постоянный множитель можно выносить за знак математического ожидания: М(СХ) = СМ(Х), где С — постоянная. 3. Математическое ожидание алгебраической суммы конечного числа п случайных величин равно алгебраической сумме их математических ожиданий: М(Х1 ± Х2 ±…± Хп) = М(Х1)±М(Х2) ±…±М(Хп). 4. Математическое ожидание произведения конечного числа п независимых случайных величин равно произведении1 их математических ожиданий: М(Х1•Х2•…•Хп) = М(Х1) •М(Х2) •…•М(Хп).
5. Если все значения случайной величины X уменьшить (увеличить) на одно и то же число с, то ее математическое ожидание уменьшится (увеличится) на то же число с: М(Х ± С) = М(Х) ± М(С) = М(Х) ± С. Следствие. Математическое ожидание отклонения значений случайной величины X от ее математического ожидания равно нулю: М[Х- М(Х)] = 0. Дисперсия ДСВ и ее свойства Для практических нужд бывает очень важно знать, как группируются значения случайных величины около ее математического ожидания. Например: 1) при стрельбе из орудия важно, чтобы снаряды ложились кучнее; 2) при измерении какой-то величины важно, чтобы ошибки измерения как можно меньше отличались от их среднего значения. Задача: Найти мат. ожидание случайной величины Х и У, которые заданы следующими распределениями:
М(Х)= -0,1*1/2 + 0,1*1/2 = 0 М(У)=-100*1/2 + 100*1/2 = 0
Математическое ожидание ничего не говорит о том, как рассеяны значения случайной величины вокруг его среднего значения (0). Рассеяние случайной величины характеризуется дисперсией. Опр. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
Теорема: Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом математического ожидания данной случайной величины
Задача. Число очков, выбиваемых при одном выстреле любого из двух стрелков, подчиняется следующим законам распределения
Кто стреляет лучше? Так как речь идет о рассеянности, то нужно найти дисперсию М(Х1) = 1 0,3 + 2 0,2 + 3 0,5 = 2,2 М(Х2) = 1 0,1 + 2 0,6 + 3 0,3 = 2,2
М(Х12) = 1 0,3 + 4 0,2 + 9 0,5 = 5,6 М(Х22) = 1 0,1 + 4 0,6 + 9 0,3 = 5,2 Д(Х1) = М(Х12) - М2(Х1) = 5,6 – 2,22 = 0,76 Д(Х2) = М(Х22) - М2(Х2) = 5,2 – 2,22 = 0,36 Ответ: лучше стреляет второй стрелок. Свойства дисперсий
Д(С) – М(С- М(С))2 = М(С - С) 2 = М(0) 2 = 0
Д(СХ) = С2 Д(Х) Доказательство: Д(СХ) = М(СХ – М(СХ))2 = М(СХ – СМ(Х))2 = М(С(Х – М(Х)))2 = С2М(Х – М(Х))2 = С2 Д(Х)
Д(Х1 ± Х2 ± … ± Хn) = Д(Х1)+ Д(X2) + … Д(Хn), где Х1, Х2, … Хn – взаимно-незасвисимые величины.
Д(С + Х) = Д(Х) Д(С+ Х) = Д(С+ Х)=Д(С) + Д(Х) = Д(Х) Постоянная не дает рассеяние ее прибавление к случайной величине Х ведет лишь к смещению всех ее значений на одну и ту же постоянную величину, а рассеяние остается прежним. Дискретных и непрерывных случайных величин
Биномиальный закон распределения Числовые характеристики Теорема: Математическое ожидание случайной величины Х, распределенной по биномиальному закону равно М(Х) = n р, а ее дисперсия Д(Х) = npq В нашей задаче М(Х) = 4/3; Д(Х) = 8/9; s(Х) = Опр. Пусть имеем множество из N элементов, которое состоит из двух подмножеств: в первом M элементов, а в другом N – М. Будем брать из множества N n элементов, в котором содержится m элементов из первого множества М n-m из второго N – М. Тогда говорят, что дискретная случайная величина Х имеет гипергеометрическое распределение, если она принимает свои значения с вероятностями
где М£ N, n £ N, n, М, N Î N
Ряд гипергеометрического распределения имеет вид:
Теорема: Математическое ожидание гипергеометрического распределения
а дисперсия Случайные величины
Дискретные и непрерывные случайные величины Понятие случайной величины является основным, неопределяемым понятием ТВ. Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно — заранее не известно). Это зависит от случая. С любой случайной величиной связывается множество ее значений. Обозначение случайных величин: X,У, Z Обозначение множества значений: х1, х2,…хn – Х Примеры случайных величин: 1) число родившихся детей в течение суток в г. Оренбурге; 2) количество бракованных изделий в данной партии; 3) число произведенных выстрелов до первого попадания; 4) дальность полета артиллерийского снаряда; 5) расход электроэнергии на предприятии за месяц.
Опр. Случайная величина, которая может принимать все значения сплошь из некоторого конечного или бесконечного пространства называется непрерывной. Опр. Случайная величина, которая может принимать отдельные изолированные значения с определенными вероятностями, называется дискретной случайной величиной (множество ее значений конечное, или бесконечное, но счетное). Так, в приведенных выше примерах 1-3 имеем дискретные случайные величины (в примерах 1,2 - с конечным множеством значений; в примере 3-е бесконечным, но счетным множеством значений); а в примерах 4,5 - непрерывные случайные величины.
Рассмотрим 2 случайные величины: Х – число выпадения герба при однократном бросании монеты {0, 1}. Y – число выпадения двух очков при однократном бросании кости {0, 1}. Р(Х>0)= ½ Р(Y>0)= 5/6 Для характеристики случайной величины недостаточно знать только множество ее значений, нужно еще знать вероятности значений, принимаемых случайной величиной
Опр. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину говорят, что она «распределена» по данному закону распределения или «подчинена» этому закону распределения. Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически. Простейшей формой задания закона распределения дискретной случайной величины Х является таблица (матрица), в которой перечислены в порядке возрастания все возможные значения случайной величины и соответствующие их вероятности, т.е.
X:
или
Такая таблица называется рядом распределения дискретной случайной величины. События Х=x1, Х=x2,..., Х=хп, состоящие в том, что в результате испытания случайная величина X примет соответственно значения х1, х2,...,хп, являются несовместными и единственно возможными (ибо в таблице перечислены все возможные значения случайной величины), т.е. образуют полную группу. Следовательно, сумма их вероятностей равна 1. Таким образом, для любой дискретной случайной величины
(Эта единица как-то распределена между значениями случайной величины, отсюда и термин «распределение»).
Ряд распределения может быть изображен графически, если по оси абсцисс откладывать значения случайной величины, а по оси ординат — соответствующие их вероятности. Соединение полученных точек образует ломаную, называемую многоугольником или полигоном распределения вероятностей. Задача 1. В лотерее разыгрывается: автомобиль стоимостью 5000 ден. ед., 4 телевизора стоимостью 250 ден. ед., 5 видеомагнитофонов стоимостью 200 ден. ед. Всего продается 1000 билетов по 7 ден. ед. Составить закон распределения чистого выигрыша, полученного участником лотереи, купившим один билет. Решение. Возможные значения случайной величины X — чистого выигрыша на один билет — равны 0-7 = -7 ден. ед. (если билет не выиграл), 200-7 = 193, 250-7 = 243, 5000-7 = 4993 ден. ед. (если на билет выпал выигрыш соответственно видеомагнитофона, телевизора или автомобиля). Учитывая, что из 1000 билетов число невыигравших составляет 990, а указанных выигрышей соответственно 5, 4 и I, и, используя классическое определение вероятности, получим: Р{Х=-7) = 990/1000=0,990; Р(Х=193) =5/1000=0,005; Р(Х=243) = 4/1000=0,004; Р(Х=4993)= 1/1000=0,001, т.е. ряд распределения
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 586; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 (1)
(1)



 ;
;
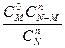


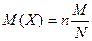 ,
, .
.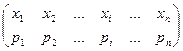
 (3.1)
(3.1)