
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моменты распределения случайной величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим распределение дискретной случайной величины:
Математическое ожидание данной величины равно 4,33. Вычислим математическое ожидание квадрата случайной величины, предварительно составив ряд распределения Х 2:
М (Х 2)=114,91.
Разница между М(Х) и М(Х 2) объясняется тем, что при возведении в квадрат возможных значений х, значение х =100 значительно увеличилось, а его вероятность осталась прежней. Переход от М(Х) к М(Х2) позволяет учесть влияние, которое оказывает на математическое ожидание то возможное значение случайной величины, которое велико и имеет малую вероятность. Поэтому возникает необходимость рассматривать математическое ожидание целой степени случайной величины. Математическое ожидание k -той степени случайной величины называется начальным моментом k -того порядка:
Для вычисления начальных моментов используются формулы:
В частности, начальный момент первого порядка равен математическому ожиданию с.в., в с.д., Дисперсия случайной величины представляет собой разность начального момента второго порядка и квадрата начального момента первого порядка:
Центральным моментом k -того порядка называется математическое ожидание k -той степени отклонения случайной величины от своего математического ожидания:
Для вычисления центральных моментов используются формулы:
Несложно показать, что Центральные моменты можно связать с начальным моментами посредством следующих равенств:
Моменты более высоких порядков встречаются редко.
В частности, центральный момент третьего порядка Если случайная величина распределена симметрично относительно своего математического ожидания, то Четвертые центральный момент служит для характеристики так называемой «крутости», т.е. островершинности или плосковершинности распределения. Эти свойства распределения описываются с помощью эксцесса. Эксцессом случайной величины Х называется величина
Контрольные вопросы
1. Что называют числовыми характеристиками (или параметрами) случайной величины? 2. Как определяется математическое ожидание случайной величины: а) дискретной; б) непрерывной? 3. Что характеризует математическое ожидание случайной величины? 4. Сформулируйте свойства математического ожидания. 5. Как определяется дисперсия случайной величины? 6. Что характеризует дисперсия случайной величины? 7. Как выглядят формулы, определяющие дисперсию, для случайной величины: а) дискретной; б) непрерывной? 8. Сформулируйте свойства дисперсии. 9. Что такое среднее квадратическое отклонение случайной величины? 10. Что характеризует среднее квадратическое отклонение и в чем смысл его введения? 11. Как определяется начальный момент k -го порядка случайной величины? 12. Как определяется центральный момент k -го порядка случайной величины? 13. Как выглядят формулы, связывающие центральные моменты случайной величины с ее начальными моментами? 14. В чем состоит вероятностный смысл начальных и центральных моментов трех первых порядков? Контрольные задания
1. Докажите свойства 3 – 4 математического ожидания для дискретной случайной величины. 2. Закон распределения дискретной случайной величины имеет вид:
Найдите математическое ожидание и дисперсию случайных величин: а) Х; б) –2 Х; в) 2 Х + 3,5. 3. Докажите свойства 3 – 5 дисперсии для дискретной случайной величины. 4. Вероятность поражения цели первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа попаданий в цель, если каждый стрелок производит: а) по одному выстрелу; б) по два выстрела. 5. Предприниматель рассматривает возможность покупки акций трех предприятий, по каждой из которых известна доходность, определяемая как отношение величины получаемого дохода за определенный период времени к цене акции и вероятности возможных значений доходности. Акции какого предприятия следует считать более доходными, если руководствоваться средним значением (математическим ожиданием) доходности?
6. Найти математическое ожидание и дисперсию случайной величины, имеющей плотность распределения: а) Случайные величины
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.174.8 (0.007 с.) |

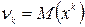 .
.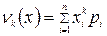 - для дискретной случайной величины
- для дискретной случайной величины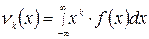 - для непрерывной случайной величины.
- для непрерывной случайной величины.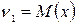 .
.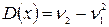 .
.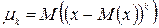 .
.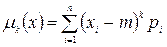 - для дискретной случайной величины
- для дискретной случайной величины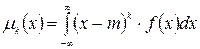 - для непрерывной случайной величины.
- для непрерывной случайной величины.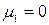 ;
; 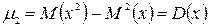 .
. ;
;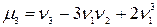 ;
;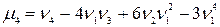 .
. Как уже было сказано ранее, числовые характеристики описывают различные особенности распределения случайных величин.
Как уже было сказано ранее, числовые характеристики описывают различные особенности распределения случайных величин.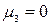 имеет размерность, равную кубу размерности случайной величины, то обычно для этой цели служит безразмерная величина, называемая коэффициентом асимметрии
имеет размерность, равную кубу размерности случайной величины, то обычно для этой цели служит безразмерная величина, называемая коэффициентом асимметрии 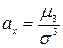 .
.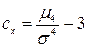 .
. Число 3 вычитается из отношения
Число 3 вычитается из отношения 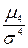 потому, что для весьма распространенного в природе нормального распределения
потому, что для весьма распространенного в природе нормального распределения 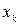
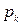
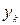
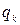
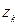
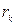
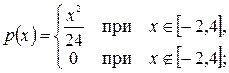 б)
б) 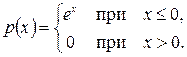
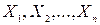 независимы, имеют одно и то же математическое ожидание a и одинаковую дисперсию
независимы, имеют одно и то же математическое ожидание a и одинаковую дисперсию 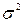 . Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение среднего арифметического этих случайных величин.
. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение среднего арифметического этих случайных величин.


