
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральная формула Муавра-Лапласа. Вероятность отклонения частоты события от его вероятности в n независимых испытанияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Достаточно часто при решении задач требуется найти вероятность того, что некоторое событие произойдет число раз, заключенное в некоторых пределах. Рассмотрим пример такой задачи.
Задача. Вероятность поражения мишени стрелком при выстреле равна 0,75. Найти вероятность того, что при 4 выстрелах стрелок поразит мишень не менее 3 раз. Решение. Найдем вероятности того, что стрелок при четырех выстрелах поразит мишень 0, 1, 2, 3 раза:
Вероятность того, что при 4 выстрелах стрелок поразит мишень не менее 3 раз выражается так: Искомую вероятность можно было найти по-другому:
В том случае, когда число испытаний достаточно велико для нахождения вероятности того, что некоторое событие произойдет число раз, заключенное в некоторых пределах, пользуются интегральной формулой Муавра-Лапласа: Если вероятность p появления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А в n опытах появится число раз, заключенное в пределах от a до b выражается формулой
где Формула (11.1) тем точнее, чем больше n. Замечания: 1. Табличные значения функции Лапласа приводятся в любых учебниках по теории вероятностей. 2. Ф (− х)=− Ф (х). 3. При х >5 Ф (х)=0,5.
Задача. Найти вероятность того, что из 1000 новорожденных мальчиков будет от 455 до 555 включительно, если вероятность рождения мальчиков равна 0,515. Решение. В данной задaче a =455, b =555, p =0,515, q =0,485, n =1000. Согласно интегральной формуле Муавра-Лапласа имеем: В некоторых задачах придётся находить вероятность того, что число наступления события А будут заключено в границах: левая а меньше, а правая b больше числа np на одно и то же число r, т.е. a = np – r, b = np + r.
т.е.
В свою очередь из формулы (11.2) можно получить формулу для нахождения Для этого обе части неравенства Таким образом, вероятность того, что абсолютная величина отклонения частоты события А от вероятности этого события p в n независимых испытаниях не превзойдет данного положительного числа ε, если вероятность наступления события А в каждом испытании постоянна выражается формулой
где
С помощью формулы (11.3) можно также находить и наименьшее число n испытаний, необходимых для того, чтобы с заданной вероятностью β отклонение частоты события А от вероятности его p по абсолютной величине не превзошла ε, если вероятность наступления события А в каждом испытании равна p.
Задача. Доля тяжёлых частиц в космическом излучении составляет в среднем 15%. Какое наименьшее число космических частиц должно быть зарегистрировано, чтобы с вероятностью 0,996 отклонение доли тяжёлых среди них от вероятности частицы быть тяжёлой не превзошло бы по абсолютной величине 0,04. Решение. В данной задaче p=0,15, q=0,85,
или или Решение последнего уравнения является n = 661. Это значит, что n = 661 – наименьшее число космических частиц должно быть зарегистрировано, чтобы с вероятностью 0,996 отклонение доли тяжёлых среди них от вероятности частицы быть тяжёлой не превзошло бы по абсолютной величине 0,04, т.е. будет заключено от 0,11 до 0,19.
Контрольные вопросы
1. Каким образом выглядит точная формула для нахождения вероятности того, что при n независимых испытаниях событие А произойдет m раз, если в каждом испытании событие А появляется с одинаковой вероятностью. 2. Какими должны быть испытания, чтобы можно было применить формулу Бернулли? 3. Что называют наивероятнейшим числом наступления события в n независимых испытаниях? Как находится это число? 4. Когда целесообразно переходить к приближенным методам вычисления по схеме Бернулли? 5. Как формулируется локальная теорема Муавра-Лапласа? 6. Какой вид имеет формула, выражающая заключение локальной теоремы Муавра-Лапласа? 7. Как формулируется интегральная теорема Муавра-Лапласа? 8. Какой вид имеет формула, выражающая заключение интегральной теоремы Муавра-Лапласа? 9. Сформулируйте свойства функции Лапласа Ф(х). 10. По какой формуле можно вычислить вероятность отклонения относительной частоты события от его вероятности? 11. Какой вид имеет формула, выражающая заключение теоремы Пуассона? 12. При каких условиях можно применять приближение Пуассона для вычислений вероятностей по схеме Бернулли?
Контрольные задания 1. Игральная кость подбрасывается 4 раза. Найти вероятность того, что два раза выпадет число очков, кратное 3. 2. Игральная кость подбрасывается 10 раз. Найти вероятность того, что четная грань выпадет ровно 3 раза. 3. Применяемый метод лечения приводит к выздоровлению в 90% случае. Какова вероятность того, что из пяти больных поправятся 4? 4. Играют два равносильных шахматиста. Что вероятнее выиграть одну партию из двух или две партии из 4? 5. На автоматическом станке можно изготовить 9 стандартных деталей из 10. Определить, чему равна вероятность того, что из 5 наудачу взятых деталей 3 окажутся стандартными? 6. Известно, что стрелок, делая 8 выстрелов, лишь раз попадает в цель. Какова вероятность того, что из 12 выстрелов не будет ни одного попадания. 7. В автопарке 70 машин, причем каждая из них может поломаться с вероятностью 0,2. Необходимо а) найти наивероятнейшее число исправных машин в автопарке и вероятность того, что в автопарке будет такое число машин; б) вероятность того, что исправными окажется не менее 50 машин; в) с вероятностью 0,95 определить границы, в которых будет находиться доля безотказно работающих машин в определенный момент времени. 8. Всхожесть семян гороха составляет в среднем 86%. Найти вероятность того, что из 2000 посаженных семян: а) число непроросших будет заключаться между 270 и 300; б) прорастут более 1700 семян. 9. Вероятность невыхода на работу из-за болезни для каждого работника предприятия, насчитывающего 500 человек, равна 0,005. Определить вероятность того, что в ближайший день: а) все работники предприятия выйдут на работу; б) не выйдет на работу хотя бы один из работников предприятия. 10. При введении вакцины против полиомиелита иммунитет создается примерно в 99,9% случаев. Какова вероятность того, что из 1000 вакцинированных детей заболеет а) один ребенок; б) хотя бы один ребенок.
Литература 1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2002. – Гл. 5. 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2002. – Гл. 3. 3. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1999. – Гл. 4.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 982; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.34.93 (0.01 с.) |

 ;
; ;
; ;
; .
. .
.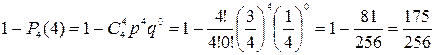 .
. , (11.1)
, (11.1) ,
, 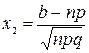 ,
,  - функция Лапласа.
- функция Лапласа.
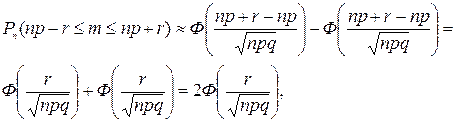
 (11.2)
(11.2) - вероятности того, что абсолютная величина отклонения частоты события А от вероятности этого события p в n независимых испытаниях не превзойдет данного положительного числа ε, если вероятность наступления события А в каждом испытании постоянна.
- вероятности того, что абсолютная величина отклонения частоты события А от вероятности этого события p в n независимых испытаниях не превзойдет данного положительного числа ε, если вероятность наступления события А в каждом испытании постоянна.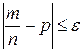 умножим на n, получим:
умножим на n, получим: 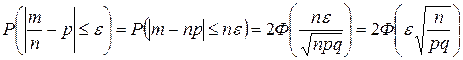 .
. , (11.3)
, (11.3) . Необходимо найти n. Имеем уравнение
. Необходимо найти n. Имеем уравнение ,
, ,
,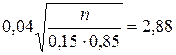 .
.


