
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция распределения. Вероятность попадания непрерывной случайной величины в заданный интервалСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ряд распределения дискретной случайной величины дает исчерпывающую характеристику с.в. Однако для непрерывной с.в. такой характеристики построить нельзя из-за бесконечности множества ее значений, заполняющих определенный интервал. Кроме того, в дальнейшем будет показано, что каждое отдельное значение непрерывной с.в. не обладает никакой отличной от нуля вероятностью. Тем не менее, различные области возможных значений непрерывной с.в. не являются одинаково вероятными. Для непрерывной с.в. также существует распределение вероятности, хотя не в том смысле, что для дискретной.
Количественная характеристика с.в.
Функция распределения – универсальная характеристика с.в., существует и для непрерывных, и для дискретных с.в. Функция распределения – одна из форм закона распределения. Функцию распределения также называют интегральной функцией распределения или интегральным законом распределения.
Свойства функции распределения: 1. 2. F(x) – неубывающая функция, т.е. если х2>x1, то F(х2)>F(x1); 3. F(x) – функция, непрерывная слева; 4. F(-¥) =0; F(¥)= 1.
Задача. Найти функцию распределения с.в. Х из задачи №2 предыдущего пункта. Решение. Ряд распределения имеет вид:
Построим функцию распределения величины Х: 1) при х £0 F(x)=P(X<x)= 0; 2) при 0< x £1 F(x)=P(X<x)=P(X =0)=0,81; 3) при 1< x £2 F(x)=P(X<x)=P(X= 0)+ P(X =1)=0,81+0,18=0,99; 4) при x >2 F(x)=P(X<x)= P(X =0)+ P(X =1)+ Р(Х =2)=0,81+0,18+0,01=1.
Пусть Х – непрерывная с.в. Вычислим вероятность того, что Х попадет в интервал (a, b), т.е. P(a<X<b). Рассмотрим три с.с.: X<a, X<b, a£X<b. Соотношение между событиями: X<b = (X<a)+(a£X<b); соотношение между вероятностями событий: Р(X<b)= Р(X<a)+Р(a£X<b), т.е. F(b)= F(a)+Р(a£X<b). Имеем: Р(a£X<b)=F(b)-F(a) (1) Или Р(a£X<b)= P(X=a)+Р(a<X<b)=F(b)-F(a) (2) В равенстве (1) положим а = х1, b = x1 + Dх. Вычислим предел при Dх®0:
P(X=a)= 0, т.е. вероятность того, что непрерывная с.в. примет какое-либо отдельное значение, равна нулю. Подставляя этот результат в равенство (2), получим, что Р(a<X<b)=F(b)-F(a), т.е. вероятность попадания непрерывной с.в. в заданный интервал равна приращению функции распределения на концах интервала. Контрольные вопросы
1. Что называют случайной величиной? 2. Определите разницу в понятиях «переменная» и «случайная величина». 3. Что называют законом распределения случайной величины? 4. Как задают закон распределения дискретной случайной величины? 5. Какую случайную величину называют дискретной? 6. Что называют рядом распределения случайной величины? 7. Что называют многоугольником распределения? 8. Как определяется функция распределения случайной величины? 9. Какими свойствами обладает функция распределения случайной величины? 10. Как с помощью функции распределения найти вероятность того, что непрерывная случайная величина попадет в интервал (a, b)?
Контрольные задания 1. Доказать свойства функции распределения F(x). 2. Дискретная случайная величина Х имеет ряд распределения
а) Чему равна вероятность того р 3? б) Построить многоугольник распределения. в) Найти функцию распределения F(x). г) Построить график функции распределения F(x).
3. Рассматривается случайная величина Х – число выпадений герба при трех подбрасываниях монеты. Построить ряд и функцию распределения этой случайной величины. Представить их графически. 4. В ящике лежит 7 шаров, среди которых 5 белых. Из ящика наудачу взято 3 шара. Найти закон распределения числа белых шаров в выборке. Представить его графически. 5. Является ли функцией распределения некоторой случайной величины каждая из следующих функций: а) в) 5. Случайная величина Х задана функцией распределения
Найдите вероятность того, что в результате испытания случайная величина Х примет значение а) равное Плотность распределения
Рассмотрим непрерывную с.в. Х с функцией распределения F(x), которая является непрерывной и дифференцируемой. Найдем приращение F(x) на интервале (x, x + Dх):
Вычислим среднюю вероятность, приходящуюся на единицу длины на этом участке, потребуем, чтобы Dх® 0, в пределе получим производную от функции распределения:
Плотностью распределения (плотностью вероятности) непрерывной с.в. Х называется функция р(x)=F`(x).
График р(x) называется кривой распределения. Плотность распределения, так же как и функция распределения, есть одна из форм закона распределения. Однако эта форма не является универсальной в отличие от функции распределения. Плотность распределения существует только для непрерывных с.в.
Свойства плотности распределения:
1. р(x)³ 0, т.е. является неотрицательной функцией, в с.д., F(x) – неубывающая функция; 2. 3. 4. Контрольные вопросы
1. Какую случайную величину называют непрерывной? 2. Как задают закон распределения непрерывной случайной величины? 3. Что называют плотностью распределения непрерывной с.в.? 4. Сформулируйте характеристические свойства плотности распределения. 5. Чему равна вероятность того, что непрерывная случайная величина примет одно определенное значение? 6. Как с помощью плотности распределения найти вероятность того, что непрерывная случайная величина попадет в интервал (a, b)?
Контрольные задания
1. Можно ли подобрать постоянную С так, чтобы функция 2. Непрерывная СВ Х имеет плотность распределения: а) Для каждого распределения необходимо: 1) найти неизвестный параметр С и построить график плотности распределения; 2) найти функцию распределения и построить ее график; 3) вычислить 4) проиллюстрировать вероятности п.3) на графике плотности распределения.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 567; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.93.167 (0.011 с.) |

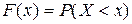
 ;
;
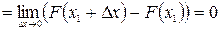 , т.е.
, т.е.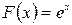 при
при 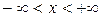 ; б)
; б) 
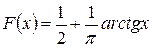 при
при 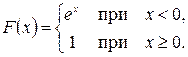
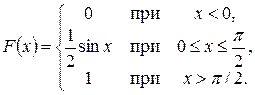
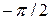 ; б) равное
; б) равное  ; в) из промежутка (
; в) из промежутка (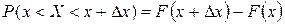 .
.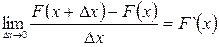 .
. Функция р(x) характеризует плотность, с которой распределяются значения с.в. в данной точке х; р(x) называется также дифференциальной функцией распределения.
Функция р(x) характеризует плотность, с которой распределяются значения с.в. в данной точке х; р(x) называется также дифференциальной функцией распределения.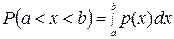 . В с.д., Р(a<X<b)=F(b)-F(a)=
. В с.д., Р(a<X<b)=F(b)-F(a)=  ;
;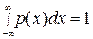 . В с.д., Р(-¥<X<¥)=
. В с.д., Р(-¥<X<¥)= 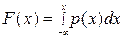 . В с.д., F(x)=Р(X<х)=Р(-¥<X<х)=
. В с.д., F(x)=Р(X<х)=Р(-¥<X<х)= 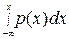 .
.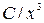 определяла плотность распределения вероятностей на интервале: а)
определяла плотность распределения вероятностей на интервале: а) 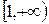 ; б)
; б) 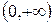 ; в)
; в) 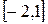 ?
?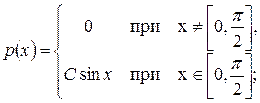 б)
б) 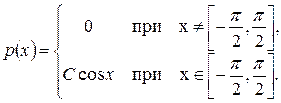
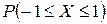 и
и 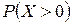 ;
;


