Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность и случайные величины
ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Методические указания и варианты заданий по теории вероятностей
Минск 2012 ************************************* Методические указания предназначены для студентов, изучающих раздел «Теория вероятностей» в рамках общего курса математики. Они ставят своей целью помочь студентам лучше усвоить теоретический и практический материал по классической теории вероятностей и теории случайных величин. В каждом разделе приводится решение типовых задач. Для закрепления материала студентам предлагается выполнить курсовое задание по рассматриваемым темам. Настоящие методические указания могут использоваться студентами на всех факультетах и специальностях, где ведется курс теории вероятностей. Предлагаемые методические указания ставят своей целью помочь студентам второго курса усвоить теоретический и практический материал по теме «Теория вероятностей». В них рассматриваются основные вопросы классической теории вероятностей и теории дискретных и непрерывных случайных величин. В каждом разделе приводится решение типовых задач. Для закрепления материала студентам предлагается выполнить задание по рассматриваемым темам. Каждому студенту группы выдаются индивидуальные задачи.
Оглавление I. КЛАССИЧЕСКАЯ ТЕОРИЯ ВЕРОЯТНОСТЕЙ 3 1. Классическое определение вероятности 3 2. Геометрические вероятности 4 3. Теоремы сложения и умножения вероятностей 5 4. Формула полной вероятности и формула Байеса 6 5. Формула Бернулли 7 II. Случайные величины 7 1. Дискретные случайные величины 8 2. Непрерывные случайные величины 9 3. Нормальный закон распределения 11 Варианты индивидуальных заданий 12 Вариант № 1 12 Вариант № 2 13 Вариант № 3 14 Вариант № 4 15 Вариант № 5 16 Вариант № 6 17 Вариант № 7 18 Вариант № 8 19 Вариант № 9 20 Вариант № 10 21 Вариант № 11 22 Вариант № 12 23 Вариант № 13 24 Вариант № 14 25 Вариант № 15 26 Вариант № 16 27 Вариант № 17 28 Вариант № 18 29 Вариант № 19 30 Вариант № 20 31 Вариант № 21 32 Вариант № 22 33 Вариант № 23 34 Вариант № 24 35 Вариант № 25 36 Вариант № 26 37 Вариант № 27 38 Вариант № 28 39 Вариант № 29 40 Вариант № 30 41 Рекомендуемая литература 43
Основным объектом классической теории вероятности является так называемое случайное событие, то есть событие, которое может произойти или не произойти в результате проведенного опыта. Числовая величина, характеризующая степень возможности данного события, называется его вероятностью.
Геометрические вероятности Если множество возможных исходов опыта можно представить в виде отрезка прямой или в виде некоторой плоской или трехмерной области, а множество исходов, благоприятных событию
где
Пример 3. В круг наудачу брошена точка. Найти вероятность того, что она не попадет в правильный треугольник, вписанный в этот круг. Решение. В этом случае мерой множества возможных исходов является площадь круга:
Формула Бернулли Рассмотрим случай, когда требуется определить не вероятность осуществления некоторого события
где Пример 7. Победу в волейбольном матче одерживает команда, выигравшая 3 партии. Найти вероятность того, что матч между командами, для которых вероятность выигрыша каждой партии равна соответственно 0,8 и 0,2, будет состоять из 5 партий. Решение. Для того, чтобы потребовалось играть пятую партию, нужно, чтобы после четырех партий счет в матче был
II. Случайные величины Во многих задачах теории вероятности удобнее оперировать не понятием случайного события, для которого существуют только две возможности: оно может произойти или не произойти в результате опыта, а понятием так называемой случайной величины, то есть величины, которая при проведенном испытании может принимать различные значения, причем заранее не известно, какие именно. Если возможный диапазон значений такой величины представляет собой конечное или счетное множество, она называется дискретной случайной величиной, а если эти значения заполняют целиком некоторый интервал — непрерывной случайной величиной. Варианты индивидуальных заданий Вариант № 1 1) Из колоды, в которой содержится 36 карт, выбираются без возвращения 2 карты. Найти вероятность того, что будут выбраны карты одной масти. 2) На плоскости проведены параллельные линии, расстояния между которыми попеременно равны 1,5 и 8 см. Найти вероятность того, что наудачу брошенный на эту плоскость круг радиуса 2,5 см не будет пересечен ни одной линией. 3) В урне содержится 7 белых, 5 черных и 8 красных шаров. Шары выбираются наугад, причем белый или черный шар в урну не возвращается, а извлеченный из урны красный шар после проверки его цвета укладывается назад в урну. Найти вероятность того, что среди первых двух последовательно вынутых шаров будет один черный. 4) Машина-экзаменатор на каждую задачу предлагает четыре ответа, из которых только один верный. В билете пять задач. Студент, не желая их решать, нажимает на клавиши случайным образом. Какова вероятность сдать зачет машине-экзаменатору, если для получения положительной оценки надо решить не менее трех задач. 5) Стрелок дважды стреляет по мишени, состоящей из трех концентрических кругов. За попадание в центральный круг дается три очка, в окружающее его кольцо — два и за попадание во внешнее кольцо — одно очко. Вероятности попадания в эти части мишени равны соответственно 0,2, 0,3 и 0,3. Найти закон распределения общего числа набранных очков. 6) В каждом из двух таймов футбольного матча обе команды вместе забивают три мяча с вероятностью 0,2, два мяча — с вероятностью 0,2, один мяч — с вероятностью 0,3 и с вероятностью 0,3 не забивают мячей. Найти математическое ожидание общего числа забитых в матче мячей. 7) Плотность вероятности непрерывной случайной величины
а) Найти значение параметра 8) Найти математическое ожидание и дисперсию нормально распределенной случайной величины Вариант № 2 1) Из полного набора костей домино наугад выбираются две. Определить вероятность того, что обе они — дубли. 2) На отрезке 3) В тире имеется пять ружей, вероятности попадания из которых равны соответственно 0,5, 0,6, 0,7, 0,8 и 0,9. Определить вероятность попадания при одном выстреле, если стрелок берет одно из ружей наудачу.
4) В волейбольном матче игра происходит до тех пор, пока одна из команд не выиграет трех партий. Вероятность победы команды 5) Во время эстафетных соревнований по биатлону спортсмену требуется поразить на огневом рубеже 5 мишеней, имея для этого 7 патронов. Вероятность попадания в мишень при одном выстреле составляет 0,8. Определить вероятность того, что все мишени будут поражены ровно семью патронами. 6) В каждом из двух таймов футбольного матча обе команды вместе забивают три мяча с вероятностью 0,1, два мяча — с вероятностью 0,2, один мяч — с вероятностью 0,4 и с вероятностью 0,3 не забивают мячей. Определить закон распределения и дисперсию общего числа забитых в матче мячей. 7) Плотность вероятности непрерывной случайной величины
а) Найти значение параметра 8) Независимые случайные величины Вариант № 3 1) Имеется урна, в которой 3 белых и 6 черных шаров. Определить вероятность того, что при выборе из урны двух шаров они окажутся разных цветов. 2) На плоскость с нанесенной на ней квадратной сеткой многократно бросается монета радиуса 3) В волейбольном матче игра происходит до тех пор, пока одна из команд не выиграет трех партий. Вероятность победы команды 4) Для контроля продукции из 3 партий деталей взята для испытания 1 деталь. Как велика вероятность обнаружения бракованной продукции, если в одной партии 2/3 деталей бракованные, а в двух других — все доброкачественные? 5) Стрелок производит восемь выстрелов по мишени, состоящей из центральной части, за попадание в которую он получает 2 очка, и остальной части, за попадание в которую стрелок получает 1 очко. Определить вероятность того, что стрелок наберет 14 очков, если вероятность попадания в центральную часть круга равна 0,1, а в остальную часть — 0,3. 6) Из полного набора костей домино наугад выбираются две. Найти закон распределения и математическое ожидание количества появлений цифры «4» на выбранных костях.
7) Плотность вероятности непрерывной случайной величины
а) Найти значение параметра 8) Случайная величина Вариант № 4 1) В розыгрыше первенства по баскетболу участвуют 18 команд, из которых случайным образом формируются две группы по 9 команд в каждой. Среди участников соревнований имеется 5 команд экстра-класса. Найти вероятность того, что все эти команды попадут в одну и ту же группу. 2) На окружности радиуса 3) Из полного набора костей домино наугад выбираются две. Найти вероятность того, что выбранные кости можно приставить друг к другу. 4) Событие 5) Из колоды в 52 карты выбираются 4 карты. Для случайной величины 6) Во время эстафетных соревнований по биатлону спортсмену требуется поразить на огневом рубеже 5 мишеней, имея для этого 7 патронов. Вероятность попадания в мишень при одном выстреле составляет 0,8. Найти дисперсию случайной величины 7) Плотность вероятности непрерывной случайной величины
а) Найти значение параметра 8) Случайная величина Вариант № 5 1) На девяти карточках написаны цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8. Две из них вынимаются наугад и укладываются на стол в порядке появления, затем читается полученное число. Найти вероятность того, что оно будет четным. 2) Какова вероятность того, что из трех взятых наудачу отрезков длины не более 3) Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями равны соответственно 0,4, 0,3 и 0,5. 4) Два баскетболиста делают по три броска мячом в корзину. Вероятности попадания мяча при каждом броске равны соответственно 0,6 и 0,7. Найти вероятность того, что у обоих будет равное количество попаданий. 5) В урне 5 белых и 3 черных шара. Из нее наудачу вынимают 3 шара. Найти закон распределения случайного числа белых шаров среди отобранных.
6) Найти дисперсию дискретной случайной величины 7) Плотность вероятности непрерывной случайной величины
а) Найти значение параметра 8) Случайная величина Вариант № 6 1) Бросаются одновременно три игральные кости. Найти вероятность того, что сумма очков на всех костях не превосходит пяти. 2) Начерчены пять концентрических окружностей, радиусы которых равны соответственно 3) В читальном зале есть 10 учебников по теории вероятностей, из них 4 в переплете. Библиотекарь взял наудачу два учебника. Найти вероятность того, что только один учебник в переплете. 4) Характеристика материала, из которого изготовлена продукция, с вероятностями 0,09; 0,16; 0,25; 0,25; 0,16 и 0,09 может находиться в шести различных интервалах. В зависимости от свойств материала вероятности получения первосортной продукции равны соответственно 0,2; 0,3; 0,4; 0,4; 0,3 и 0,2. Определить вероятность получения первосортной продукции. 5) Стрелок производит 7 выстрелов по различным мишеням, причем выстрелы по каждой мишени производятся до первого попадания в нее, после чего выстрелы производятся по следующей мишени. Вероятность попадания при каждом выстреле равна 0,8. Найти закон распределения случайной величины 6) В каждом из трех периодов хоккейного матча команда забивает две шайбы с вероятностью 0,4, одну шайбу — с вероятностью 0,3 и не забивает шайб с вероятностью 0,3. Определить дисперсию количества шайб, забитых в матче. 7) Плотность вероятности непрерывной случайной величины
а) Найти значение параметра 8) Случайная величина Вариант № 7 1) Из колоды в 52 карты выбираются случайным образом без возвращения 2 карты. Найти вероятность того, что будут выбраны карты разных значений. 2) Найти вероятность того, что монета радиуса 3) Имеется три ящика, в первом из которых 6 стандартных и 3 бракованных детали, во втором — 5 стандартных и 4 бракованных и в третьем — 7 стандартных и 4 бракованных. Найти вероятность того, что если из каждого ящика выбрать по детали, то среди них будет одна стандартная и две бракованных. 4) Имеется 5 урн следующего состава: две урны состава 5) Из последовательности чисел 1, 2, 3, …, 99, 100 выбирают наугад с возвращением 10. Найти вероятность того, что среди них кратных 7 будет не более двух. 6) В каждом из трех периодов хоккейного матча команда забивает две шайбы с вероятностью 0,3, одну шайбу — с вероятностью 0,5 и не забивает шайб с вероятностью 0,2. Найти закон распределения числа шайб, забитых в матче. 7) Плотность вероятности непрерывной случайной величины
а) Найти значение параметра 8) Браковка шариков для подшипников производится следующим образом: если шарик проходит через отверстие диаметра Вариант № 8 1) Из полного набора костей домино наугад выбираются две. Найти вероятность того, что обе они — не дубли. 2) На отрезке 3) Орудие осуществляет стрельбу по цели, для поражения которой необходимо попасть в нее дважды. Вероятность попадания в цель при первом выстреле равна 0,5; в дальнейшем она не меняется при промахах, но после первого попадания вероятность промаха при дальнейших выстрелах уменьшается вдвое. Боекомплект составляет 5 снарядов. Найти вероятность того, что цель будет поражена, если первый выстрел был точным. 4) Известно, что 96 % выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0,98 и нестандартную — с вероятностью 0,05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту. 5) Во время эстафетных соревнований по биатлону требуется поразить на огневом рубеже 5 мишеней, имея для этого 7 патронов. Вероятность попадания в мишень при одном выстреле составляет 0,7. Определить вероятность того, что при стрельбе на двух огневых рубежах спортсмен поразит все мишени, израсходовав при этом 12 патронов. 6) Из урны, содержащей 3 белых и 4 черных шара, извлекаются без возвращения шары до появления белого шара. Найти закон распределения и математическое ожидание случайного числа вынутых из урны шаров. 7) Плотность вероятности непрерывной случайной величины
а) Найти значение параметра 8) Средняя температура в квартире в период отопительного сезона равна 22°C, а ее среднее квадратическое отклонение — 0,5°C. С вероятностью, не меньшей 0,96, найти границы, в которых заключена температура в квартире, считая ее нормально распределенной случайной величиной. Вариант № 9 1) Имеется урна, в которой 4 белых, 3 красных и 7 черных шаров. Определить вероятность того, что при выборе из урны двух шаров они окажутся белыми. 2) Из отрезка [–1; 2] наудачу взяты два числа. Найти вероятность того, что их сумма больше единицы, а произведение меньше единицы. 3) В ящике содержится 6 деталей типа 4) Производится 4 независимых опыта, в каждом из которых событие 5) Стрелок дважды стреляет по мишени, состоящей из трех концентрических кругов. За попадание в центральный круг дается три очка, в окружающее его кольцо — два, и за попадание во внешнее кольцо — одно очко. Вероятности попадания в эти части мишени равны соответственно 0,3, 0,3 и 0,1. Найти закон распределения общего числа набранных очков. 6) Из колоды в 32 карты выбирается 4 карты. Найти математическое ожидание числа карт трефовой масти среди отобранных. 7) Плотность вероятности непрерывной случайной величины
а) Найти значение параметра 8) Случайная величина Вариант № 10 1) Из последовательности чисел 2) На отрезке 3) Два баскетболиста делают по три броска мячом в корзину. Вероятности попадания мяча при каждом броске равны соответственно 0,6 и 0,7. Найти вероятность того, что у первого баскетболиста будет больше попаданий, чем у второго. 4) Литье в болванках поступает из двух заготовительных цехов: 65 % из первого и 35 % — со второго. При этом материал первого цеха имеет 15 % брака, а второго — 25 %. Найти вероятность того, что одна взятая наугад болванка без дефектов. 5) В партии из 12 деталей имеется 3 бракованных. Из партии случайным образом извлечены 3 детали. Составить ряд распределения числа доброкачественных деталей среди отобранных. 6) Стрелок производит 7 выстрелов по различным мишеням, причем выстрелы по каждой мишени производятся до первого попадания в нее, после чего выстрелы производятся по следующей мишени. Вероятность попадания при каждом выстреле равна 0,5. Найти дисперсию числа пораженных мишеней. 7) Плотность вероятности непрерывной случайной величины
а) Найти значение параметра 8) Найти математическое ожидание и дисперсию нормально распределенной случайной величины Вариант № 11 1) Имеется пять билетов стоимостью по одному рублю, три билета по три рубля и два билета по пять рублей. Наугад берутся три билета. Найти вероятность того, что хотя бы два из них имеют одинаковую стоимость. 2) Какова вероятность того, что сумма трех наудачу взятых отрезков, длина каждого из которых не превосходит 3) Имеется 10 одинаковых по виду урн, из которых в 9 находится по два черных и два белых шара, а в одной — пять белых и один черный шар. Из урны, взятой наудачу, извлечен белый шар. Какова вероятность того, что он извлечен из урны, содержащей пять белых шаров? 4) В волейбольном матче игра происходит до тех пор, пока одна из команд не выиграет трех партий. Вероятность победы команды 5) Во время эстафетных соревнований по биатлону спортсмену требуется поразить на огневом рубеже 5 мишеней, имея для этого 7 патронов. Вероятность попадания в мишень при одном выстреле составляет 0,6. Найти закон распределения и математическое ожидание числа пораженных мишеней. 6) В каждом из трех матчей хоккейного турнира команда с вероятностью 0,2 одерживает победу, получая за нее 2 очка, с вероятностью 0,4 играет вничью, получая 1 очко, и с вероятностью 0,4 терпит поражение, не получая за это очков. Найти дисперсию общего числа набранных очков. 7) Плотность вероятности непрерывной случайной величины
а) Найти значение параметра
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 752; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.109 (0.016 с.) |
 — как часть этой области, то вероятность рассматриваемого события определяется следующим образом:
— как часть этой области, то вероятность рассматриваемого события определяется следующим образом:
 — длина отрезка (площадь или объем области), задающего множество возможных исходов, а
— длина отрезка (площадь или объем области), задающего множество возможных исходов, а  — соответствующая мера множества благоприятных исходов.
— соответствующая мера множества благоприятных исходов. а мерой множества благоприятных исходов — разность площадей круга и треугольника:
а мерой множества благоприятных исходов — разность площадей круга и треугольника:  . Следовательно, вероятность заданного события равна
. Следовательно, вероятность заданного события равна
 опытов. Будем считать при этом, что вероятность
опытов. Будем считать при этом, что вероятность  раз (неважно, в каких именно опытах), определяется по формуле Бернулли:
раз (неважно, в каких именно опытах), определяется по формуле Бернулли:
 — вероятность появления
— вероятность появления  — вероятность того, что в данном опыте событие
— вероятность того, что в данном опыте событие 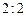 . Следовательно, каждая из команд должна выиграть любые две партии из четырех. Если
. Следовательно, каждая из команд должна выиграть любые две партии из четырех. Если  есть вероятность выигрыша в каждой партии для первой команды, а
есть вероятность выигрыша в каждой партии для первой команды, а  — вероятность ее проигрыша, то, применяя формулу Бернулли, найдем, что
— вероятность ее проигрыша, то, применяя формулу Бернулли, найдем, что
 имеет вид:
имеет вид:
 . б) Построить график функции распределения
. б) Построить график функции распределения  . в) Найти
. в) Найти  ,
,  и
и  . г) Найти вероятность того, что случайная величина
. г) Найти вероятность того, что случайная величина  и
и  . Построить кривую распределения и найти ее максимум.
. Построить кривую распределения и найти ее максимум. длины
длины 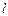 наудачу поставлены две точки
наудачу поставлены две точки  и
и 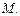 Найти вероятность того, что точка
Найти вероятность того, что точка  чем к точке
чем к точке  в каждой партии равна 0,4. Определить вероятность того, что в матче победит команда
в каждой партии равна 0,4. Определить вероятность того, что в матче победит команда 
 имеют нормальный закон распределения с параметрами
имеют нормальный закон распределения с параметрами  ,
,  . Рассматривается случайная величина
. Рассматривается случайная величина  . С помощью неравенства Чебышева оценить вероятности
. С помощью неравенства Чебышева оценить вероятности  ,
,  .
. , в результате чего установлено, что в 40 % случаев монета не пересекает ни одной стороны квадрата. Оценить размер сетки.
, в результате чего установлено, что в 40 % случаев монета не пересекает ни одной стороны квадрата. Оценить размер сетки. победит со счетом 3:0.
победит со счетом 3:0.
 ,
,  . Найти: а) плотность вероятности случайной величины
. Найти: а) плотность вероятности случайной величины  ,
,  ,
,  ; б) вероятности
; б) вероятности 
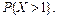
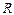 наудачу поставлены три точки
наудачу поставлены три точки  Какова вероятность того, что треугольник
Какова вероятность того, что треугольник  — остроугольный?
— остроугольный? наступает в том случае, если событие
наступает в том случае, если событие 
 ,
,  . Найти: а) плотность вероятности
. Найти: а) плотность вероятности  б) математическое ожидание и дисперсию; в) вероятности
б) математическое ожидание и дисперсию; в) вероятности 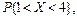


 и
и 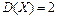 . Найти
. Найти  и
и  .
.
 . Круг радиуса r и два кольца с внешними радиусами
. Круг радиуса r и два кольца с внешними радиусами  и
и  заштрихованы. В круге радиуса
заштрихованы. В круге радиуса 

 . Найти:а) математическое ожидание и дисперсию; б) вероятность
. Найти:а) математическое ожидание и дисперсию; б) вероятность  .
. , пересечет не более одной стороны клетки.
, пересечет не более одной стороны клетки. — по 1 белому и 4 черных шара; одна урна состава
— по 1 белому и 4 черных шара; одна урна состава  — 2 белых и 3 черных шара; две урны состава
— 2 белых и 3 черных шара; две урны состава 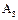 — по 3 белых и 2 черных шара. Из одной наудачу выбранной урны взят шар, он оказался белым. Найти вероятность того, что этот шар был вынут из урны третьего состава.
— по 3 белых и 2 черных шара. Из одной наудачу выбранной урны взят шар, он оказался белым. Найти вероятность того, что этот шар был вынут из урны третьего состава.
 , но не проходит через отверстие диаметра
, но не проходит через отверстие диаметра 
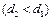 , то шарик считается годным. Если какое-либо из этих условий нарушается, то шарик бракуется. Считается, что диаметр шарика — случайная величина, распределенная по нормальному закону с параметрами
, то шарик считается годным. Если какое-либо из этих условий нарушается, то шарик бракуется. Считается, что диаметр шарика — случайная величина, распределенная по нормальному закону с параметрами  ,
,  , где
, где 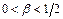 . Каким следует выбрать коэффициент
. Каким следует выбрать коэффициент  , чтобы брак составлял не более 3 % всей продукции?
, чтобы брак составлял не более 3 % всей продукции?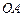 длины
длины  . Найти вероятность того, что длина отрезка
. Найти вероятность того, что длина отрезка  будет меньше расстояния от точки
будет меньше расстояния от точки  до ближайшей к ней точке.
до ближайшей к ней точке.
 . Детали выбираются наугад, причем вынутая деталь типа
. Детали выбираются наугад, причем вынутая деталь типа 
 .
. ,
,  , …,
, …,  — произвольное целое число?
— произвольное целое число? .
.
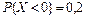 и
и  . Построить кривую распределения и найти ее максимум.
. Построить кривую распределения и найти ее максимум. будет больше
будет больше