

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Коэффициент корреляции и проверка его значимости. Линейная регрессия и прогноз
Похожие статьи вашей тематики
В п. 29 – 32 были даны определения теоретического коэффициента корреляции и коррелированных величин, перечислены свойства коэффициента корреляции.
Точечной оценкой теоретического коэффициента корреляции  является выборочный коэффициент корреляции является выборочный коэффициент корреляции  , который находится по формуле: , который находится по формуле:
 , ,
где  и и  – выборочные средние; – выборочные средние;  , ,  – выборочные средние квадратические отклонения переменных Х и Y соответственно; – выборочные средние квадратические отклонения переменных Х и Y соответственно;  – выборочное среднее значение переменной – выборочное среднее значение переменной  . .
Можно показать, что выборочный коэффициент корреляции обладает всеми свойствами теоретического коэффициента корреляции, т.е.
1. Для любых переменных Х и Y абсолютная величина коэффициента корреляции не превосходит единицы, т.е. 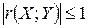 ; ;
2. Если Х и Y независимы, то  = 0; = 0;
3. Абсолютная величина коэффициента корреляции равна единице тогда и только тогда, когда между переменными Х и Y существует линейная связь, т.е.  , где , где  и b – некоторые постоянные величины. При этом и b – некоторые постоянные величины. При этом  = 1, если a>0, и = 1, если a>0, и  = -1, если a<0. = -1, если a<0.
В силу всего сказанного выше, можно заключить, что изучение вида линейной зависимости между переменными Х и Y имеет смысл лишь тогда, когда величина  значима или существенна, т.е. не очень близка к нулю. Если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность, то заключение о тесноте линейной зависимости между переменными, полученное по выборочным данным, в известной мере может быть распространено и на генеральную совокупность. Для достижения этой цели может быть использован критерий, основанный на распределении Стьюдента. значима или существенна, т.е. не очень близка к нулю. Если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность, то заключение о тесноте линейной зависимости между переменными, полученное по выборочным данным, в известной мере может быть распространено и на генеральную совокупность. Для достижения этой цели может быть использован критерий, основанный на распределении Стьюдента.
Для оценки достоверности коэффициента корреляции проверяется гипотеза Н0 об отсутствии линейной корреляционной связи между переменными в генеральной совокупности (против альтернативной гипотезы, состоящей в том, что зависимость между Х и Y значима), т.е. Н0:  , по следующей схеме: , по следующей схеме:
1. Вычисляется статистика  отклонения выборочного коэффициента корреляции от генерального коэффициента корреляции отклонения выборочного коэффициента корреляции от генерального коэффициента корреляции  , где n – число наблюдений; , где n – число наблюдений;
2. По таблице критических точек распределения Стьюдента на уровне значимости  и при числе степеней свободы и при числе степеней свободы  находим значение находим значение  ; ;
3. Если не выполняется неравенство  , гипотеза Н0 отвергается, т.е. выборочный коэффициент корреляции существенно отличается от нуля, что свидетельствует о достоверности коэффициента корреляции. , гипотеза Н0 отвергается, т.е. выборочный коэффициент корреляции существенно отличается от нуля, что свидетельствует о достоверности коэффициента корреляции.
Задача. Выборочный коэффициент корреляции  между переменными Х и Y при числе наблюдений n = 50 оказался равным 0,74. Оценить достоверность коэффициента корреляции между переменными Х и Y при числе наблюдений n = 50 оказался равным 0,74. Оценить достоверность коэффициента корреляции  на 5% уровне значимости. на 5% уровне значимости.
Решение. Найдем статистику критерия по формуле  : :
 . .
Для уровня значимости  и числа степеней свободы и числа степеней свободы  , находим критическое значение статистики , находим критическое значение статистики 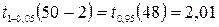 . Поскольку . Поскольку 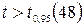 , то коэффициент корреляции достоверен на 5% уровне значимости. , то коэффициент корреляции достоверен на 5% уровне значимости.
Как было отмечено в п. 32, при линейной зависимости между переменными Х и Y уравнение регрессии Y на Х представляет собой прямую
 , ,
где а и b – неизвестные коэффициенты.
Исходя из выборочных данных, методом наименьших квадратов находят следующие оценки неизвестных коэффициентов уравнения:
 , ,
 , ,
где  , ,  , ,  , , 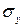 , r определяются формулами, приведенными в предыдущих разделах. , r определяются формулами, приведенными в предыдущих разделах.
Оценкой теоретической прямой регрессии является выборочная прямая регрессии
 . .
Чтобы подчеркнуть, что речь идет о выборочном условном среднем, прямую, определяемую последним уравнением, обозначают 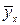 . .
Точность линейной аппроксимации выборочных данных визуально можно оценить, сравнив поле рассеяния с графиком выборочной прямой регрессии.
Наилучший точечный линейный прогноз среднего значения зависимой переменной Y при любом фиксированном значении независимой переменной Х = х0 задается при помощи выборочного уравнения регрессии Y на Х:
 . .
Задача 2. В детской поликлинике была собрана следующая информация о связи между временем реакции ребенка Y и его возрастом (в месяцах) X:
| Возраст (мес.)
|
|
|
|
| | Время реакции (сек)
| 1,5
| 0,8
| 0,5
| 0,4
|
Используя полученные данные, необходимо вычислить выборочный коэффициент корреляции, проанализировать степень тесноты и направление связи между изучаемыми переменными. Предскажите время реакции ребенка в возрасте 4,5 месяца.
Решение. По данным таблицы найдем выборочные средние и среднее квадратические отклонения переменных Х и Y:




 
Вычислим выборочное среднее значение величины  : :
 . .
Выборочный коэффициент корреляции найдем по формуле:

Полученное значение выборочного коэффициента корреляции показывает, что между переменными Х и Y существует достаточно тесная связь, близкая к линейной. Поскольку  , то эта связь убывающая, т.е. по мере увеличения возраста, уменьшается время реакции ребенка. , то эта связь убывающая, т.е. по мере увеличения возраста, уменьшается время реакции ребенка.
Выборочное уравнение линейной регрессии Y на Х будем искать в виде:
 , ,
и в данной задаче оно таково:
 . .
Подставляя в последнее соотношение значение х = 4,5 (мес.), найдем ожидаемое время реакции ребенка:
 (сек). (сек).
Контрольные вопросы
1. В чем состоит разница в понятиях «теоретический коэффициент корреляции» и «выборочный коэффициент корреляции»?
2. Как определяется выборочный коэффициент корреляции?
3. Сформулируйте свойства выборочного коэффициента корреляции.
4. Что означает значимость теоретического коэффициента корреляции?
5. Как проверить значимость теоретического коэффициента корреляции по известному значению выборочного коэффициента корреляции, если имеется выборка большого объема?
6. Какой вид имеет уравнение регрессии переменной Y на Х в случае линейной регрессионной модели?
7. Как оценивается теоретическая прямая регрессии переменной Y на Х?
8. Как определяется точечный прогноз среднего значения зависимой переменной Y при заданном значении независимой переменной Х?
Контрольные задания
1. Исследуется зависимость между количеством Х покупателей в ювелирном магазине и количеством Y проданных товаров. За 10 дней наблюдения получили следующие данные:
| Количество покупателей
|
|
|
|
|
|
|
|
|
|
| | Число покупок
|
|
|
|
|
|
|
|
|
|
|
Оцените тесноту и направление между количеством покупателей в магазине и количеством проданных товаров с помощью выборочного коэффициента корреляции. Оцените значимость корреляции между рассматриваемыми переменными с надежностью 0,95. Построить модель линейной регрессии. Если в магазине было 80 покупателей, сколько было продано товара?чеством проданных товаров с помощью выборочного коэффициент
2. По результатам тестирования школьников по чтению и арифметике на основе набранных баллов получены следующие данные:
Оцените тесноту и направление связи между знаниями школьника по чтению и по арифметике с помощью выборочного коэффициента корреляции. Оцените значимость корреляции между рассматриваемыми переменными с надежностью 0,99.
Литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2002. – Гл. 18, п.п. 1 – 9, гл. 19 п. 22.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2002. – Гл. 12, п. 1; гл. 13, п. 12.
ТЕСТЫ
| 1.
| Монета подбрасывается только один раз. Событие А – «выпал герб», Событие В - «выпала цифра». Вероятность события А·В равна…
| 1.
|
| | 2.
| ½
| | 3.
| ¼
| | 4.
|
|
| 2.
| У мальчика в левом кармане три конфеты «Белочка» и одна «Маска». В правом – две «Белочки» и две «Маски». Он достал две конфеты из одного кармана, и оказалось, что одна из них «Белочки», а другая – «Маска». Какова вероятность того, что он достал конфеты из левого кармана?
| 1.
| 3/7
| | 2.
|
| | 3.
| 4/7
| | 4.
| ½
|
| 3.
| Три человека производят выстрелы в мишень. Каждый из них попадает в мишень с вероятностью 0,4. Какова вероятность того, что в мишень попадут двое из трёх?
| 1.
| 0,432
| | 2.
| 0,288
| | 3.
| 0,72
| | 4.
|
|
| 4.
| Какова вероятность того, что при 10 подкидываниях монеты герб выпадет ровно 5 раз?
| 1.
| 0,25
| | 2.
| 0,75
| | 3.
| 0,5
| | 4.
|
|
| 5.
| Партия транзисторов, среди которых 10% дефективных, поступает на проверку. Схема проверки такова, что с вероятностью 0,95 обнаруживает дефект (если он есть), и существует вероятность 0,03, что исправный транзистор будет признан дефективным. Случайно выбранный из партии транзистор был признан дефективным. Вероятность того, что на самом деле транзистор исправен, равна…
| 1.
| 
| | 2.
| 
| | 3.
| 
| | 4.
| 
|
| 6.
| Какова вероятность того, что при 2-х подкидываниях монеты 2 раза выпадет герб?
| 1.
|
| | 2.
| 0,25
| | 3.
| 0,5
| | 4.
| 0,75
|
| 7.
| У короля есть 100 сундуков с золотыми монетами, каждый из которых содержит 100 монет. В каждом сундуке есть фальшивая монета. Король берет из каждого сундука по одной монете. Какова вероятность того, что король найдет хотя бы одну фальшивую монету?
| 1.
| 0,01
| | 2.
| 0,63
| | 3.
| 0,99
| | 4.
| 0,5
|
| 8.
| Вероятности банкротства двух предприятий, производящих разнотипную продукцию, равны 0,1 и 0,15. Вероятность банкротства сразу двух этих предприятий, равна…
| 1.
| 0,25
| | 2.
| 0,015
| | 3.
| 0,765
| | 4.
| 0,15
|
| 9.
| Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,8 и 0,75. Вероятность того, что цель будет поражена, равна
| 1.
| 0,4
| | 2.
| 0,55
| | 3.
| 0,6
| | 4.
| 0,95
|
| 10.
| Опыт состоит в том, что стрелок производит три выстрела по мишени. Событие  - «попадание в мишень при k-ом выстреле (k=1, 2, 3)». Выразить событие «не меньше двух попаданий при трех выстрелах» через события - «попадание в мишень при k-ом выстреле (k=1, 2, 3)». Выразить событие «не меньше двух попаданий при трех выстрелах» через события  (k=1, 2, 3) (k=1, 2, 3)
| 1.
| 
| | 2.
| 
| | 3.
| 
| | 4.
| 
|
| 11.
| В мастерской работают два мотора, независимо друг от друга. Вероятность того, что в течение часа первый мотор не потребует внимания мастера, равна 0,85, а для второго мотора эта вероятность равна 0,8. Вероятность того, что в течение часа хотя бы один из моторов потребует внимания мастера, равна…
| 1.
|  . .
| | 2.
|  . .
| | 3.
| 
| | 4.
| 0,15·0,2
|
| 12.
| Система радиолокационных станций ведет наблюдение за группой объектов, состоящей из 5 единиц. Каждый из объектов может быть потерян (независимо от других) с вероятностью 0,1. Вероятность того, что будет потеряно более трех объектов, равна…
| 1.
| 
| | 2.
| 
| | 3.
| 
| | 4.
| 
|
| 13.
| При неограниченном значении числа независимых опытов, в каждом из которых случайное событие А может появиться с одинаковой вероятностью 0,4, относительная частота появления события А сходится по вероятности к…
| 1.
|
| | 2.
| 0,6
| | 3.
| 0,4
| | 4.
| ∞
|
| 14.
| Игральная кость подбрасывается ровно один раз. Вероятность того, что на верхней грани выпадет не менее 5 очков, равна
| 1.
| 5/6
| | 2.
| 1/6
| | 3.
| ½
| | 4.
| 1/3
|
| 15.
| Бросают две монеты. События «герб на первой монете» и «герб на второй монете» являются…
| 1.
| несовместными и независимыми
| | 2.
| совместными и независимыми
| | 3.
| несовместными и зависимыми
| | 4.
| совместными и зависимыми
|
| 16.
| Разыскивая специальную книгу, студент решил обойти три библиотеки. Для каждой библиотеки одинаково вероятно, есть в ее фондах книга или нет. И если книга есть, то одинаково вероятно занята она другими читателями или нет. Библиотеки комплектуются независимо одна от другой. Какова вероятность того, что студент получит книгу?
| 1.
| 37/64
| | 2.
| 27/64
| | 3.
| 1/2
| | 4.
| 1/3
|
| 17.
| В первой урне 6 белых и 4 черных шара, а во второй урне – 7 черных и 3 белых шара. Из наудачу взятой урны вынут один шар. Найти вероятность того, что этот шар окажется белым.
| 1.
| 0,4
| | 2.
| 0,45
| | 3.
| 0,15
| | 4.
| 0,9
|
| 18.
| С первого станка на сборку поступает 40%, а со второго станка 60% всех деталей. Среди деталей, поступивших с первого станка 1% бракованных, со второго станка – 2%. Вероятность того, что деталь, поступившая на сборку, является бракованной равна…
| 1.
| 0,014
| | 2.
| 0,015
| | 3.
| 0,03
| | 4.
| 0,016
|
|
| Вероятность выиграть две партии из 4 у равносильного противника (ничья не в счет) равна…
| 1.
| 1/8
| | 2.
| 3/8
| | 3.
| 1/16
| | 4.
| 1/2
|
| 20.
| Наиболее вероятное число выпадений герба при 5 подбрасываниях монеты равно…
| 1.
|
| | 2.
|
| | 3.
|
| | 4.
| 3 и 2
|
| 21.
| Страхуется 2000 автомобилей. Считается, что каждый из них может попасть в аварию с вероятностью 0,001. Для вычисления вероятности того, что количество аварий среди всех застрахованных автомобилей не превзойдет 100, следует воспользоваться
| 1.
| формулой Пуассона
| | 2.
| интегральной формулой Муавра-Лапласа
| | 3.
| формулой Бейеса
| | 4.
| формулой полной вероятности
|
| 22.
| Вероятность появления события А в 10 независимых испытаниях, проводимых по схеме Бернулли, равна 0,8. Дисперсия числа появлений этого события равна
| 1.
| 0,16
| | 2.
| 1,6
| | 3.
| 0,08
| | 4.
|
|
| 23.
| Ряд распределения случайной величины Х:
| Х
|
|
|
|
|
| | Р
| 0,05
| 0,15
| р3
| 0,25
| 0,35
| Найти р 3
| 1.
| 0,1
| | 2.
| 0,2
| | 3.
| 0,3
| | 4.
| 0,4
|
| 24.
| Дан ряд распределения дискретной случайной величины:
Найти математическое ожидание случайной величины
| 1.
| 4,3
| | 2.
| 0,9
| | 3.
| 3,0
| | 4.
|
|
| 25.
| При одном опыте событие А появляется с вероятностью 0,7. Математическое ожидание числа появлений события А в одном опыте равно…
| 1.
| 0,3
| | 2.
| 0,5
| | 3.
| 0,7
| | 4.
|
|
| 26.
| Дан ряд распределения дискретной случайной величины:
Найти математическое ожидание квадрата величины
| 1.
| 14,6
| | 2.
| 1,8
| | 3.
|
| | 4.
| 1,46
|
| 27.
| Дан ряд распределения дискретной случайной величины:
Найти дисперсию этой случайной величины
| 1.
| 3,69
| | 2.
| 24,6
| | 3.
| 29,7
| | 4.
|
|
| 28.
| Математическое ожидание случайной величины Х равно 2, математическое ожидание случайной величины 3 Х +1 равно…
| 1.
|
| | 2.
|
| | 3.
|
| | 4.
|
|
| 29.
| Дисперсия случайной величины Х равна 2, дисперсия случайной величины 3 Х -1 равна…
| 1.
|
| | 2.
|
| | 3.
|
| | 4.
|
|
| 30.
| Производится 10 независимых испытаний, вероятность появления события B в каждом из этих испытаний, равна 0,4. Математическое ожидание числа появлений события В равно
| 1.
| 2,4
| | 2.
| 0,410
| | 3.
|
| | 4.
| 100,4
|
| 31.
| Случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка, называют...
| 1.
| дискретной
| | 2.
| неопределенной
| | 3.
| непрерывной
| | 4.
| относительной
|
|
| Непрерывная случайная величина распределена равномерно на отрезке [-11; 20]. Найти Р(X<0)
| 1.
| 11/31
| | 2.
| 10/31
| | 3.
| 5/16
| | 4.
| 11/32
|
|
| Непрерывная случайная величина распределена равномерно на отрезке [-11; 26]. Найти Р(X>-4)
| 1.
| 29/37
| | 2.
| 15/19
| | 3.
| 19/38
| | 4.
| 30/37
|
|
| Если плотность распределения вероятности случайной величины Х представлена функцией  , то дисперсия Х равна… , то дисперсия Х равна…
| 1.
|
| | 2.
|
| | 3.
|
| | 4.
|
|
|
| Время безотказной работы элемента распределено по показательному закону  при при  (t – время). Вероятность того, что элемент проработает безотказно более 100 ч, равна… (t – время). Вероятность того, что элемент проработает безотказно более 100 ч, равна…
| 1.
| 
| | 2.
| 
| | 3.
| 
| | 4.
| 
|
|
| Время безотказной работы элемента распределено по показательному закону  при при  (t – время, ч). Среднее время безотказной работы элемента, равно… (t – время, ч). Среднее время безотказной работы элемента, равно…
| 1.
| 0,02
| | 2.
|
| | 3.
|
| | 4.
|
|
|
| Функция  представляет собой плотность распределения вероятности некоторой случайной величины на интервале (0; 2) при а, равном… представляет собой плотность распределения вероятности некоторой случайной величины на интервале (0; 2) при а, равном…
| 1.
|
| | 2.
|
| | 3.
| 1/3
| | 4.
| 1/2
|
|
| Плотность распределения случайной величины Х равна  . Найти D(1-Х) . Найти D(1-Х)
| 1.
|
| | 2.
| -2
| | 3.
|
| | 4.
|
|
|
| Плотность распределения случайной величины Х равна  . Найти М(1-Х) . Найти М(1-Х)
| 1.
|
| | 2.
| -2
| | 3.
|
| | 4.
|
|
|
| Если случайная величина Х подвержена показательному распределению с плотностью  то математическое ожидание Х равно…
то математическое ожидание Х равно…
| 1.
| е
| | 2.
|
| | 3.
| 1/5
| | 4.
| 1/25
|
|
| График плотности распределения вероятности непрерывной случайной величины Х, распределенной равномерно в интервале (-1; 4), имеет вид:
 Значение параметра а равно…
Значение параметра а равно…
| 1.
| 0,2
| | 2.
|
| | 3.
| 0,25
| | 4.
| 0,33
|
|
| Если случайная величина Х равномерно распределена в интервале (1; 5), то М(2Х) равна…
| 1.
|
| | 2.
|
| | 3.
|
| | 4.
|
|
|
| При обследовании признака генеральной совокупности получены следующие значения: 0, 1, 2, 1, 0, 4, 2, 1, 3, 7, 5, 1, 2, 0, 5, 7, 5, 4. Найти значение эмпирической функции распределения при х=2.
| 1.
| 1/6
| | 2.
|
| | 3.
| 7/18
| | 4.
| 5/9
|
|
| При обследовании признака генеральной совокупности получены следующие значения: 1, 3, 5, 2, 7, 5. Известно, что признак подчинен показательному распределению с М(Х)=  . Найти параметр а. . Найти параметр а.
| 1.
| 23/6
| | 2.
| 6/23
| | 3.
| 23/2
| | 4.
| 2/23
|
|
| Произведено 5 измерений без систематических ошибок некоторой случайной величины (в мм): 4; 5; 8; 9; 11. Несмещенная оценка математического ожидания равна …
| 1.
|
| | 2.
| 7,6
| | 3.
| 9,25
| | 4.
| 7,4
|
|
| Произведено 3 измерения без систематических ошибок над некоторой физической случайной величиной (в мм): 10; 12; 14. Несмещенная оценка дисперсии равна…
| 1.
|
| | 2.
|
| | 3.
|
| | 4.
|
|
|
| Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид…
| 1.
| (10; 10,9)
| | 2.
| (8,4; 10)
| | 3.
| (8,5; 11,5)
| | 4.
| (8,6; 9,6)
|
|
| Произведено 4 измерения без систематических ошибок некоторой случайной величины (в кг): 5; 6; 9; 12. Несмещенная оценка математического ожидания равна …
| 1.
|
| | 2.
|
| | 3.
| 8,25
| | 4.
| 8,5
|
|
| Из генеральной совокупности извлечена выборка объема n = 50:
Найти n4
| 1.
|
| | 2.
|
| | 3.
|
| | 4.
|
|
|
| Из генеральной совокупности извлечена выборка объема n = 50, полигон частот имеет вид:

Число вариант xi = 3 в выборке равно…
| 1.
|
| | 2.
|
| | 3.
|
| | 4.
|
|
|
| Из генеральной совокупности извлечена выборка объема n = 50:
Средняя выборочная равна…
| 1.
|
| | 2.
| 2,5
| | 3.
| 126/50
| | 4.
| 133/50
|
|
| При обследовании признака генеральной совокупности получены следующие значения: 0, 1, 2, 1, 0, 4, 2, 1, 3, 7, 5, 1, 2, 0, 5, 7, 5, 4. Несмещенная оценка генеральной средней равна…
| 1.
|
| | 2.
| 10/3
| | 3.
| 25/9
| | 4.
| 5/2
|
|
|
 При выборке объема n = 100 построена гистограмма частот. Значение а равно… При выборке объема n = 100 построена гистограмма частот. Значение а равно…
| 1.
|
| | 2.
|
| | 3.
|
| | 4.
|
|
|
|
При выборке объема n построена гистограмма частот.
Значение n равно  … …
| 1.
|
| | 2.
|
| | 3.
|
| | 4.
|
|
|
| В результате опытов над случайной величиной оказалось, что абсолютная величина отклонения ее значений от математического ожидания не превосходит утроенного среднего квадратического отклонения. Выдвигается гипотеза о том, что рассматриваемая случайная величина подчинятся…
| 1.
| Показательному закону распределения
| | 2.
| Нормальному закону распределения
| | 3.
| Закону равномерной плотности
| | 4.
| Закону распределения Пуассона
|
|
| Коэффициент корреляции случайных величин Х и Y равен 0,7. Между случайными величинами Х и Y…
|
| не существует корреляционной зависимости
| |
| существует возрастающая корреляционная зависимость
| |
| существует убывающая корреляционная зависимость
| |
| существует убывающая функциональная зависимость
|
|
| С надежностью 0,95 доверительный интервал для математического ожидания нормально распределенного признака генеральной совокупности имеет вид: (10; 10,8). С какой вероятностью математическое ожидание попадает в указанный интервал?
| 1.
|
| | 2.
| 0,05
| | 3.
| 0,95
| | 4.
|
|
|
| В результате обработки опытного материала обширного объема вычислены два первых эмпирических момента: 0,168 и 1,69 (соответственно). Эмпирическое распределение выровнено с помощью нормального закона вида…
| 1.
| 
| | 2.
| 
| | 3.
| 
| | 4.
| 
|
|
| Если нулевая гипотеза имеет вид: Н0: а =5, то конкурирующей может быть гипотеза
| 1.
| Н1: а ≥5
| | 2.
| Н1: а ≠5
| | 3.
| Н1: а <15
| | 4.
| Н1: а ≤5
|
|
| На уровне значимости α=0,01 проверяется нулевая гипотеза Н0: признак генеральной совокупности подчиняется нормальному закону распределения. Если в результате проверки Н0 будет отвергнута, то вероятность ошибки решения такого рода равна
| 1.
|
| | 2.
| 0,01
| | 3.
| 0,99
| | 4.
|
|
ГЛОССАРИЙ
| Вероятность случайного события
|
– численная мера степени объективной возможности этого события.
| | Гистограмма
| – ступенчатая фигура, состоящая из прямоугольников, основаниями которой служат частичные интервалы длиною h, а высоты равны отношению  (плотность частоты). (плотность частоты).
| | Дискретные случайные величины
| – случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить.
| | Дисперсия
| – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
| | Доверительный интервал
| – интервал, который покрывает неизвестный параметр с заданной надежностью.
| | Достоверное событие
| – событие, которое в результате опыта должно обязательно произойти.
| | Закон распределения случайной величины
|
– всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
| | Корреляционный момент
случайных величин
|
– математическое ожидание произведения отклонений случайных величин от их математических ожиданий.
| | Коррелированные случайные величины
|
– случайные величины, корреляционный момент которых отличен от нуля.
| | Коэффициент корреляции случайных величин
|
– отношение корреляционного момента к произведению средних квадратических отклонений.
| | Критерий согласия
| – критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
| | Математическое
ожидание дискретной
случайной величины
|
– сумма произведений всех возможных значений случайной величины и их вероятностей.
| | Невозможное случайное событие
|
– событие, которое в данном опыте не должно произойти.
| | Независимые случайные величины
|
– случайные величины, закон распределения каждой из которых не зависит от того, какие значения приняла другая величина.
| | Независимые случайные события
|
– события, вероятность каждого из которых не зависит от того, произошло другое событие или нет.
| | Непрерывная случайная величина
|
– случайная величина, возможные значения которой непрерывно заполняют некоторый промежуток.
| | Несмещенная оценка
| – статистическая оценка, математическое ожидание которой равно оцениваемому параметру.
| | Несовместные случайные события
|
– события, появление одного из которых в данном опыте исключает появление другого.
| | Полная группа событий
| – множество событий данного опыта таких, что в результате него должно появиться хотя бы одно из них.
| | Произведение событий
| – событие, состоящее в одновременном появлении этих событий.
| | Равновозможные случайные события
|
– такие события, что в данном опыте ни одно из них не является более возможным, чем другое.
| | Ряд распределения
| – перечень всех возможных значений случайной величины и соответствующих им вероятностей.
|
| Поделиться:
|
|



 является выборочный коэффициент корреляции
является выборочный коэффициент корреляции  , который находится по формуле:
, который находится по формуле: ,
, и
и  – выборочные средние;
– выборочные средние;  ,
,  – выборочные средние квадратические отклонения переменных Х и Y соответственно;
– выборочные средние квадратические отклонения переменных Х и Y соответственно;  – выборочное среднее значение переменной
– выборочное среднее значение переменной  .
.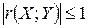 ;
; = 0;
= 0; , где
, где  и b – некоторые постоянные величины. При этом
и b – некоторые постоянные величины. При этом  , по следующей схеме:
, по следующей схеме: отклонения выборочного коэффициента корреляции от генерального коэффициента корреляции
отклонения выборочного коэффициента корреляции от генерального коэффициента корреляции  и при числе степеней свободы
и при числе степеней свободы  находим значение
находим значение  ;
; , гипотеза Н0 отвергается, т.е. выборочный коэффициент корреляции существенно отличается от нуля, что свидетельствует о достоверности коэффициента корреляции.
, гипотеза Н0 отвергается, т.е. выборочный коэффициент корреляции существенно отличается от нуля, что свидетельствует о достоверности коэффициента корреляции. :
: .
. и числа степеней свободы
и числа степеней свободы  , находим критическое значение статистики
, находим критическое значение статистики 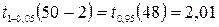 . Поскольку
. Поскольку 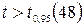 , то коэффициент корреляции достоверен на 5% уровне значимости.
, то коэффициент корреляции достоверен на 5% уровне значимости. ,
, ,
, ,
, ,
, 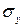 , r определяются формулами, приведенными в предыдущих разделах.
, r определяются формулами, приведенными в предыдущих разделах. .
.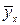 .
. .
.





 :
: .
.
 , то эта связь убывающая, т.е. по мере увеличения возраста, уменьшается время реакции ребенка.
, то эта связь убывающая, т.е. по мере увеличения возраста, уменьшается время реакции ребенка. ,
, .
. (сек).
(сек).



 - «попадание в мишень при k-ом выстреле (k=1, 2, 3)». Выразить событие «не меньше двух попаданий при трех выстрелах» через события
- «попадание в мишень при k-ом выстреле (k=1, 2, 3)». Выразить событие «не меньше двух попаданий при трех выстрелах» через события 



 .
.
 .
.





 , то дисперсия Х равна…
, то дисперсия Х равна…
 при
при  (t – время). Вероятность того, что элемент проработает безотказно более 100 ч, равна…
(t – время). Вероятность того, что элемент проработает безотказно более 100 ч, равна…




 представляет собой плотность распределения вероятности некоторой случайной величины на интервале (0; 2) при а, равном…
представляет собой плотность распределения вероятности некоторой случайной величины на интервале (0; 2) при а, равном…
 . Найти D(1-Х)
. Найти D(1-Х)
 то математическое ожидание Х равно…
то математическое ожидание Х равно…
 Значение параметра а равно…
Значение параметра а равно…
 . Найти параметр а.
. Найти параметр а.

 При выборке объема n = 100 построена гистограмма частот. Значение а равно…
При выборке объема n = 100 построена гистограмма частот. Значение а равно… …
…




 (плотность частоты).
(плотность частоты).



