
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства статистических оценокСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для оценки одного и того же параметра Всякая оценка неизвестного параметра Поскольку наблюдения над случайным признаком Х предполагаются независимыми, то их результаты
Оценка
В противном случае оценка называется смещенной. Условие несмещенности также называют условием отсутствия систематических ошибок, и его смысл состоит в том, что при многократном использовании вместо параметра Если оценка является смещенной, то, вычислив ее математическое ожидание и введя поправочный коэффициент, можно получить несмещенную оценку. Докажем, что несмещенной оценкой генеральной (теоретической) средней является выборочная средняя В самом деле, в силу свойств математического ожидания
Теперь рассмотрим выборочную дисперсию
Таким образом, Так как
В силу независимости
Подставляя выражение для
Таким образом, выборочная дисперсия является смещенной оценкой для теоретической (генеральной) дисперсии Несмещенной оценкой теоретической дисперсии
называемая исправленной выборочной дисперсией. Докажем, что если известна генеральная средняя а, то несмещенной оценкой теоретической дисперсии
В самом деле, используя свойства математического ожидания, определение дисперсии, равенства
Оценка
Имеют место следующие факты:
Требование состоятельности оценки является по существу минимальным требованием, которое обычно предъявляется к оценкам. Условие состоятельности представляется необходимым для того, чтобы оценка имела практический смысл, так как в противном случае увеличение объема исходной информации не будет приближать нас к оцениваемой величине. Представим себе, что мы имеем две несмещенные и состоятельные оценки Оценка
Контрольные вопросы
1. В чем состоит разница в понятиях: выборочная характеристика и теоретическая характеристика? 2. Что такое точечная оценка параметра распределения? 3. Как определяется выборочная средняя? 4. Что характеризует выборочная средняя? 5. Как определяется выборочная дисперсия? 6. Что характеризует выборочная дисперсия? 7. Какие требования предъявляются к оценкам параметров? 8. Как определяется несмещенная статистическая оценка? 9. Что является несмещенной оценкой для: а) теоретической (генеральной) средней; б) теоретической (генеральной) дисперсии? 10. Как определяется состоятельная статистическая оценка? 11. Как определяется эффективная статистическая оценка?
Контрольные задания
1. В результате 10 измерений длины стержня одним прибором получены следующие результаты (в мм): 100, 95, 103, 94, 102, 98, 95, 105, 106, 96. Найти оценки: а) длины стрежня; б) дисперсии и среднего квадратического отклонения ошибок прибора. Предполагается, что среднее значение результатов измерений примерно совпадает с истинной длиной стрежня. 2. Даны результаты 10 независимых исследований одной и той же величины прибором, не имеющим систематических ошибок (в мм): 369, 378, 420, 385, 401, 372, 383, 405, 370, 415. Определить несмещенную оценку дисперсии ошибок измерений, если истинная длина измеряемой величины: а) известна и равна 375 мм; б) неизвестна.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 800; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 можно построить, исходя из выборки
можно построить, исходя из выборки  различные оценки. Например, чтобы оценить математическое ожидание
различные оценки. Например, чтобы оценить математическое ожидание 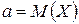 , можно рассматривать либо среднее арифметическое из выборочных данных, либо полусумму наибольшего и наименьшего наблюдений, либо какую-нибудь другую функцию от выборки. В связи с этим возникает вопрос о требованиях, которые следует предъявлять к оценкам параметров распределения, чтобы они были в каком-то определенном смысле наилучшими. Эти требования выражаются следующими свойствами оценок: несмещенностью, состоятельностью и эффективностью.
, можно рассматривать либо среднее арифметическое из выборочных данных, либо полусумму наибольшего и наименьшего наблюдений, либо какую-нибудь другую функцию от выборки. В связи с этим возникает вопрос о требованиях, которые следует предъявлять к оценкам параметров распределения, чтобы они были в каком-то определенном смысле наилучшими. Эти требования выражаются следующими свойствами оценок: несмещенностью, состоятельностью и эффективностью. от выборочных данных
от выборочных данных  . Величины
. Величины  можно рассматривать как случайные величины. Поэтому и оценка
можно рассматривать как случайные величины. Поэтому и оценка  ,
, .
. параметра
параметра  .
. равно нулю.
равно нулю. .
. .
.

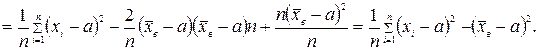
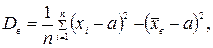 где
где  (i = 1, 2, …, k) и
(i = 1, 2, …, k) и 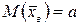 , то по свойствам математического ожидания и дисперсии получаем
, то по свойствам математического ожидания и дисперсии получаем
 .
.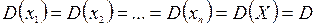 имеем
имеем .
. в выражение для
в выражение для  , получаем
, получаем .
. .
. является величина
является величина ,
, .
. .
. при любом сколь угодно малом
при любом сколь угодно малом  .
. к их общему математическому ожиданию
к их общему математическому ожиданию  ;
; сходится по вероятности при
сходится по вероятности при 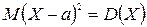 :
: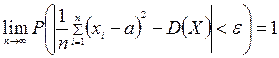 ;
; и
и  неизвестного параметра
неизвестного параметра  , совпадающая для несмещенных оценок (для которых
, совпадающая для несмещенных оценок (для которых  ) с дисперсией
) с дисперсией  .
. . Для несмещенных оценок
. Для несмещенных оценок 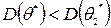 . В силу сказанного выше наилучшей оценкой параметра
. В силу сказанного выше наилучшей оценкой параметра 


