Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция №5 Тема: Основы теории оценок и норм.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные понятия. Показанные спортсменами результаты (в частности, результаты тестов), во-первых, выражаются в разных единицах измерения (время, расстояние и т.д.), и поэтому непосредственно не сопоставимы друг с другом; во-вторых, сами по себе не указывают, насколько удовлетворительно состояние спортсмена (например, время бега на 100м, равное 12.0 сек рассматривается как хорошее или плохое в зависимости от того, о ком идет речь). Поэтому результаты превращают в оценки (очки, баллы, отметки, разряды и т.д.). Последовательность действий при оценивании видна из приведенной схемы, в которую включены также этапы тестирования и измерения результатов теста. Рис. Схема оценивания спортивных результатов и результатов тестов.
Закон преобразования спортивных результатов в очки называют шкалой оценок. Оценкой (или педагогической оценкой) называется унифицированная мера успеха в каком-либо задании, в частном случае – в тесте. Процесс определения оценок называется оцениванием. Он состоит из следующих стадий: 1. Подбирается шкала, с помощью которой возможен перевод результатов теста в очки. 2. В соответствии с выбранной шкалой результаты теста преобразуются в очки (баллы). 3. Полученные очки сравниваются с нормами, и выводится итоговая оценка. Основные задачи оценивания: 1. по результатам оценивания сопоставляются разные достижения в соревновательных упражнениях; 2. сопоставляются достижения в различных видах спорта, уравниваются оценки за достижения одинаковой трудности в разных видах или дисциплинах. 3. создаются научно-обоснованные нормы.
Перевести результаты тестирования в баллы можно разными способами. На практике для этого часто используется ранжирование или упорядочение зарегистрированного ряда измерений. Преобразование результатов тестирования в оценки проводится также помощью использования специальных шкал. Шкала оценок может быть представлена: · таблицей; · графиком функции; · математической формулой. Все шкалы можно разделить на две группы: 1. Пропорциональные (линейные) шкалы. 2. Нелинейные шкалы.
Существует четыре типа таких шкал. 1. Пропорциональная шкала. При ее использовании равные приросты результатов в тесте поощряются равными приростами в баллах. Так, в этой шкале, уменьшение времени бега на 0.1с оценивается в 20 очков. Их получит спортсмен, бегавший 100м за 12.8 сек. и пробежавший эту дистанцию за 12.7 сек, и спортсмен, улучивший свой результат с 12.1 до 12 сек. Она используется в современном пятиборье, конькобежном спорте, гонках на лыжах, лыжном двоеборье, биатлоне др.
2. Прогрессирующая шкала. Здесь равные приросты результатов оцениваются по-разному. Чем выше абсолютные приросты, тем больше прибавка в оценке. Так, за улучшение результата в беге на 100м с 12.8 до 12.7 сек. дается 20 очков, с 12,7 до 12.6 сек. –30 очков. Применяется в плавании, отдельных видах лёгкой атлетики, в тяжёлой атлетике.
3. Регрессирующая шкала. В этой шкале равные приросты результатов в тестах также оцениваются по-разному, но чем выше абсолютные приросты, тем меньше прибавка в оценке. Так, за улучшение результатов в беге на 100м с 12.8 до 12.7 сек, дается 20 очков, с 12.7 до 12.6 сек. –18 очков, с 12.1 до 12.0 сек. – 4 очка. Шкалы такого типа приняты в некоторых видах легкоатлетических прыжков и метаний. 4. Сигмовидная (или S- образная) шкала. Здесь выше всего оцениваются приросты в средней зоне, а улучшение низких или очень высоких результатов поощряется слабо. Так, за улучшение результатов с 12.8 до 12.7 и с 12.1 до 12.0 начисляется по 10 очков, а с 12.5 до 12.4 сек – 30 очков. В спорте такие шкалы не используются, но они применяются при оценке физической подготовленности. В спортивной практике наиболее часто применяются шкалы, для которых эквивалентными принято считать результаты в различных видах спорта, в равной степени доступные одинаковому проценту спортсменов одного возраста и пола. Исходя из этого, считают все мировые рекорды эквивалентными, независимо от вида спорта, и оценивают их одинаковым числом очков, например 100. Составив список сильнейших спортсменов по каждому виду спорта, считают эквивалентными также сотые результаты, т.е. всем таким спортсменам начисляют один балл. Каждая из этих шкал имеет свои достоинства, так и недостатки. Рассмотрим несколько примеров использования шкал. Пример первый. Известно, что разносторонне физически подготовленным человеком считается тот, кто хорошо бегает, плавает, прыгает, подтягивается и т.д. Оценка результатов в этих упражнениях должна не только объективно отразить уровень подготовленности, но и настроить человека на совершенствование своей физической подготовленности. Она может проводиться с помощью следующих шкал: 1.Сигмовидной. В этом случае, чтобы получить максимально возможную сумму баллов в комплексе тестов, нужно показывать в каждом из них средние результаты. Если же в одном-двух тестах результаты будут предельные, а в остальных низкие, суммарная оценка уменьшится. При такой шкале оценок нельзя иметь низкие результаты в каких-либо тестах - они будут резко снижать сумму баллов. У этой шкалы есть и недостатки: если человек показывает высокие результаты во всех тестах, то оценки перестают стимулировать его; достижения в тестах растут быстрее, чем оценки за них. 2. Пропорциональной. В этой шкале нет предыдущего недостатка. Стимул получить большую оценку за более высокий результат сохраняется во всем диапазоне достижений. Плохо в этой шкале другое: низкие результаты, например, в плавании, можно компенсировать высокими в беге. В этом случае говорить о разносторонней физической подготовленности не приходится. Пример второй. В тех случаях, когда возникает необходимость поощрить подготовку спортсменов высокого класса (например, МСМК) используется прогрессирующая шкала. Этот же критерии, но примененный к оценкам результатов первенства города, будет неэффективным: основной контингент участников – спортсмены - разрядники принесут меньше очков, чем один спортсмен высокого класса, что снизит массовость. Пример третий. Спортивные многоборья создавались как виды, в которых нужно показывать высокие результаты в разных спортивных упражнениях. Оценивать достижения здесь лучше всего по регрессирующей шкале, и вот почему. Пока результаты во всех видах невысоки, приросты в баллах значительны. На уровне высшего спортивного мастерства регрессирующая шкала будет стимулировать тренировочную работу в отстающих видах: недобор очков в них оказывается большим, чем дополнительные очки за очень высокие достижения в одном-двух видах многоборья. Выбор и обоснование критериев. Оценка, как унифицированный измеритель спортивных результатов, может быть эффективной, если она справедлива и с пользой применяется в практике. Это зависит от критериев, на основе которых оцениваются результаты. При выборе критериев следует иметь в виду вопросы: 1) какие результаты должны быть положены в нулевую точку шкалы и 2) как оценивать промежуточные и максимальные достижения. Целесообразно использование следующих критериев: 1. Равенство временных интервалов, необходимых для достижения результатов, соответствующих одинаковым разрядам в разных видах спорта. 2. Равенство объемов нагрузок, которые необходимо затратить на достижение одинаковых квалификационных норм в разных видах спорта. 3. Равенство мировых рекордов в разных видах спорта. 4. Равные соотношения между числом спортсменов, выполнивших разрядные нормы в разных видах спорта. Применение шкал оценок в практике. Для оценок результатов тестирования используется несколько шкал:
х - показанный результат - средний результаты,
В мировой практике используются и другие стандартные шкалы.
2. Перцентильная шкала. В основе этой шкалы лежит следующая операция: каждый спортсмен из группы получает за свой результат (в соревнованиях или тестах) столько очков, сколько процентов спортсменов он опередил. Таким образом, оценка победителя 100 очков, оценка последнего – 0 очков. Перцентильная шкала наиболее пригодна для оценки результатов больших групп спортсменов. В таких группах статистическое распределение результатов нормальное (или почти нормальное). Это значит, что очень высокие и низкие результаты показывают единицы из группы, а средние - большинство. Главное достоинство этой шкалы - простота. Единственное, что здесь нужно вычислить - какое количество результатов спортсменов укладывается в один перцентиль (или сколько перцентилей приходится на одного человека). Перцентиль- это интервал шкалы. При 100 спортсменах в одном перцентиле один результат; при 50 – один результат укладывается в два перцентиля (т.е. если спортсмен обошел 30 человек, он получает 60 очков). Перцентильные шкалы относятся к сигмовидным шкалам. Простота обработки результатов и наглядность этой шкалы обусловили ее широкое применение в практике.
3. Шкала ГЦОЛИФКа. Рассмотренные выше шкалы используются для оценки результатов группы спортсменов, и цель их применения заключается в определении межиндивидуальных различий (в баллах). В практике спорта тренеры постоянно сталкиваются еще с одной проблемой: оценка результатов периодического тестирования одного и того же спортсмена в разные периоды цикла или этапа подготовки. Для этого предложена шкала ГЦОЛИФКа, выраженная в формуле:
где: К — оценка результата в баллах или очках.
Смысл такого подхода заключается в том, что результат теста рассматривается не как отвлеченная величина, а во взаимосвязи с лучшим и худшим результатами, показанными в этом тесте спортсменом. Лучший результат всегда оценивается в 100 очков, худший в 0 очков. Эту шкалу целесообразно применять для оценки вариативных показателей. Нормой в спортивной метрологии называется граничная величина результатов теста, на основе которой производится классификация спортсменов. Есть официальные нормы (например, разряды в ЕСК) и неофициальные (их устанавливают тренеры или специалисты в области спортивной тренировки) для классификации спортсменов по каким- либо качествам (свойствам, способностям). Существует три вида норм: 1) сопоставительные; 2) индивидуальные; 3) должные. 1. Сопоставительные нормы устанавливаются после сравнения достижений людей, принадлежащих к одной и той же совокупности. Сопоставительные нормы ранжируют людей внутри совокупности, но ничего не говорят о совокупности в целом. Эти нормы можно разрабатывать непосредственно на основе показателей средних величин и стандартов. Например, в таблице 1 приведены 7 классификационных групп, границы которых определяются средним квадратическим отклонением. Нормы такого рода удобны тем, что сразу ясно, какому проценту исследуемых лиц они посильны.
Таблица 1. Возможные градации оценок и норм.
В практике физического воспитания широко распространены возрастные нормы. Эти нормы относятся к сопоставительным нормам. Реализация такого подхода приведена в таблице №2:
Таблица №2. Классификация мужчин по уровню работоспособности (по К. Куперу).
2. Индивидуальные нормы основаны на сравнении показателей одного и того же спортсмена в разных состояниях. Эти нормы имеют исключительно важное значение для индивидуализации тренировки во всех видах спорта. Необходимость их определения возникла вследствие различий в тренированности спортсменов. Градация индивидуальных норм устанавливается с помощью тех же статистических процедур. За среднюю норму здесь можно принимать показатели тестов, соответствующие среднему результату в соревновательном упражнении. 3. Должные нормы устанавливаются по основанию требований, которые предъявляют человеку условия жизни, профессия и т.д. Поэтому во многих случаях они опережают действительные показатели. В спортивной практике должные нормы устанавливаются так: 1) определяются информативные показатели подготовленности спортсмена; 2) измеряются результаты в соревновательном упражнении и соответствующие им достижения в тестах; 3) рассчитывается уравнение регрессии типа у= кх + в, где x – должный результат в тесте, а у – прогнозируемый результат в соревновательном упражнении. Должные результаты в тесте и являются должной нормой: ее необходимо достичь, и только тогда можно будет показывать запланированный результат в соревнованиях. Требования к пригодности норм: 1. Если нормы пригодны только для той совокупности, для которой разработаны, такая пригодность называется релевантностью, а нормы — релевантными. 2. Если нормы установлены при обследовании типичной выборки исследуемых, т.е. пригодны для всей генеральной совокупности, они называются репрезентативными. 3. Нормы должны быть современными, т.е. пересматриваться один раз в 4 года.
Основная литература: [1,2,3,4,5,6] Дополнительная литература: [1,2]
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 749; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.67 (0.008 с.) |


 1. Стандартная шкала. В основе ее лежит пропорциональная шкала. Свое название она получила потому, что масштабом в ней служит стандартное (среднеквадратическое) отклонение. Наиболее распространена Т-шкала. Здесь средний результат приравнивается к 50 очкам, а вся формула выглядит следующим образом:
1. Стандартная шкала. В основе ее лежит пропорциональная шкала. Свое название она получила потому, что масштабом в ней служит стандартное (среднеквадратическое) отклонение. Наиболее распространена Т-шкала. Здесь средний результат приравнивается к 50 очкам, а вся формула выглядит следующим образом: где Т- оценка результата в тесте
где Т- оценка результата в тесте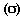 - стандартное отклонение.
- стандартное отклонение.