
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция №3 Тема: Определение основных статистических показателей (ОСП) для характеристики совокупностейСодержание книги
Поиск на нашем сайте
Наиболее распространенными характеристиками совокупности являются: 1) среднее арифметическое 2) среднее квадратическое (или стандартное) отклонение 3) стандартная ошибка среднего арифметического 4) коэффициент вариации (V). 1. Средним арифметическим называется частное от деления суммы всех значений вариант рассматриваемой совокупности на их число (n):
Среднее арифметическое обладает следующими свойствами: а) измеряется в тех же единицах, что и основные варианты; б) если каждое число совокупности уменьшить (увеличить) на одно и то же число, то ее среднее уменьшится (увеличится) на это же число; в) если каждое число совокупности увеличить (уменьшить) в несколько раз, то ее среднее увеличится (уменьшится) в такое же число раз; г) сумма отклонений статистических данных совокупности от их точного среднего всегда равна нулю:
В основе среднего квадратического отклонения лежит сопоставление каждой варианты
Величина
1. Стандартное отклонение всегда измеряется в тех же единицах измерения, что и основные варианты.
Стандартная ошибка средней вычисляется по формуле:
В современной научной литературе средняя арифметическая представляется вместе с ошибкой репрезентативности:
4. Коэффициент вариации (V).Изложенные выше характеристики совокупности (средняя арифметическая и среднее квадратическое отклонение) имеют один недостаток: они дают показатель изменчивости признака в именованных величинах, а не в относительных. Поэтому сопоставление (или сравнение) разноименных признаков по этим параметрам невозможно. В этом случае удобно пользоваться коэффициентом изменчивости признака, который выражается в относительных величинах, а именно в процентах, и вычисляется по формуле:
Чем больше V, тем более изменчив признак. Значения коэффициента вариации, невыходящие за пределы 10%, принято считать нормальными.
Основная литература: [1,2,3,4,5,6] Дополнительная литература: [1,2]
|
|||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 2383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.53.112 (0.006 с.) |


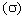 ;
; ;
; (1)
(1)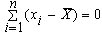
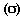 . Основной мерой статистического измерения изменчивости признака у членов совокупности служит среднее квадратическое отклонение
. Основной мерой статистического измерения изменчивости признака у членов совокупности служит среднее квадратическое отклонение 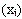 со средней арифметической данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений
со средней арифметической данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений  ), имеющих знак " - ", будет погашаться суммой отклонений, имеющих знак
), имеющих знак " - ", будет погашаться суммой отклонений, имеющих знак  Отклонение вариант от своей средней арифметической выражает изменчивость признака. Если бы изменчивость признака у членов совокупности отсутствовала, тогда разность
Отклонение вариант от своей средней арифметической выражает изменчивость признака. Если бы изменчивость признака у членов совокупности отсутствовала, тогда разность 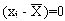 . Но т.к.
. Но т.к. 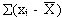 всегда равна нулю, то для измерения изменчивости берут отклонение в квадрате, т.е.
всегда равна нулю, то для измерения изменчивости берут отклонение в квадрате, т.е. 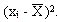 Если просуммировать квадраты отклонений, то эта сумма не будет равна нулю. А чтобы получить коэффициент, способный измерить изменчивость, берут среднее отклонение из выражения:
Если просуммировать квадраты отклонений, то эта сумма не будет равна нулю. А чтобы получить коэффициент, способный измерить изменчивость, берут среднее отклонение из выражения: (2)
(2)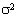 называется дисперсией. Тогда среднее квадратическое отклонение имеет следующую формулу:
называется дисперсией. Тогда среднее квадратическое отклонение имеет следующую формулу: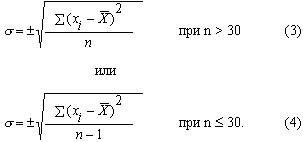
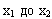 , которые отстоят от средней арифметической на величину от
, которые отстоят от средней арифметической на величину от 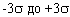 . За пределами
. За пределами 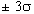 находятся только 0,3% всех членов совокупности.
находятся только 0,3% всех членов совокупности. (5)
(5) . (6)
. (6)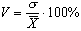 , (7)
, (7)


