
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная регрессия. Прямые линии среднеквадратической регрессииСодержание книги
Поиск на нашем сайте Рассмотрим систему двух зависимых случайных величин Х и Y. Положим, что Назовем функцию Справедливо следующее утверждение. Линейная регрессия Y на Х имеет вид Прямая Решив задачу оптимизации величины При r = 0 Аналогично, прямая среднеквадратической регрессии Х на У имеет вид Проанализировав уравнения линий среднеквадратической регрессии Y на Х и Х на Y, отметим, что обе прямые проходят через одну и ту же точку (mx, my), которая называется центром совместного распределения Х и Y. При
При r = -1 имеем также два равносильных уравнения:
Контрольные вопросы
1. Сформулируйте условие независимости составляющих для: а) непрерывной с.в. (Х; Y); б) дискретной с.в. (Х; Y). 2. Как выглядят формулы для безусловных характеристик составляющих а) непрерывной с.в. (Х; Y); б) дискретной с.в. (Х; Y): математического ожидания и дисперсии составляющих)? 3. Как выглядят формулы для условных характеристик составляющих а) непрерывной с.в. (Х; Y); б) дискретной с.в. (Х; Y): математического ожидания и дисперсии составляющих)? 4. Для каких целей используются корреляционный момент и коэффициент корреляции? 5. Сформулируйте свойства: а) корреляционного момента; б) коэффициента корреляции. 6. Какие случайные величины называются: а) коррелированными? б) некоррелированными? 7. Будут ли случайные величины некоррелированными, если они независимы? 8. Будут ли случайные величины коррелированными, если они зависимы? 9. Будут ли случайные величины независимы, если они некоррелированы? 10. Будут ли случайные величины зависимы, если они коррелированы? 11. Приведите пример случайных величин, для которых равносильны понятия независимости и некоррелированности. 12. Что называется прямой среднеквадратической регрессии Y на Х? 13. Что называется коэффициентом регрессии Y на Х? 14. Что называется остаточной дисперсией случайной величины Y относительно случайной величины Х? 15. Что можно сказать о характере зависимости между с.в. Х и Y при: а) r = 0; б) r = 1; в) r = -1? 16. Что называется центром совместного распределения Х и Y?
Контрольные задания
Непрерывная случайная величина (Х; Y) равномерно распределена в области D, где D – треугольник с вершинами в точках О(0, 0), А (2, 0), С (0, 3). 1. Найдите плотность совместного распределения Х и Y; 2. Найдите плотности распределения составляющих Х и Y; 3. Найти математические ожидания и дисперсии составляющих Х и Y (безусловные); 4. Найти условную плотность распределения, условное математическое ожидание составляющей Х при Y = 1; 5. Найдите корреляционный момент и коэффициент корреляции Х и Y; 6. Исследуйте зависимость Х и Y.
Литература 4. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2002. – Гл. 14. 5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2002. – Гл. 8. 6. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1999. – Гл. 8.
Закон больших чисел Во введении было отмечено, что теория вероятностей изучает закономерности, свойственные массовым случайным явлениям. Единичные явления, которые наблюдаем вместе с их индивидуальными особенностями, скрывают закономерности, которые имеют место при наблюдении большого числа аналогичных явлений. Суть одной из таких закономерностей состоит в том, что конкретные особенности каждого случайного явления почти не сказываются на среднем результате массы таких явлений. Эта устойчивость средних представляет собой результат действия закона больших чисел. Под законом больших чисел в теории вероятностей понимается ряд теорем, в каждой из которых при тех или иных условиях устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным. Знание закона распределения случайной величины позволяет находить вероятности различных событий, относящихся к этой случайной величине. На практике зачастую известны лишь числовые характеристики с.в. В этом случае невозможно найти значения вероятностей событий, связанных с этой с.в., но можно оценить сверху или снизу вероятности различных отклонений с.в., используя только числовые характеристики с.в. Пусть имеется случайная величина Х с математическим ожиданием m и дисперсией D. Неравенство Чебышева утверждает, что каково бы ни было положительное число
Задача. Оценить вероятность того, что отклонение с.в. Х от своего среднего значения М (Х) не превысит «трех Решение. В формуле (33.1) положим
Напомним, что согласно правилу «трех
Неравенство Чебышева представляет собой важный и удобный инструмент теории вероятностей. Важность этого неравенства вытекает из его универсальности, поскольку оценка вероятности в нем не зависит от закона распределения с.в. Неравенство Чебышева даёт только верхнюю границу данного отклонения. Выше этой границы вероятность не может быть ни при каком законе распределения. Рассмотрим последовательность случайных величин Х1, Х2, …, Хn. Говорят, что последовательность Х1, Х2, …, Хn сходится по вероятности к с.в. Х, если для любого Законом больших чисел называют теоремы, утверждающие, что при определенных ограничениях на с.в., разность между средней арифметической случайных величин и средней арифметической их математических ожиданий сходится к нулю по вероятности. Одной из простейших, но вместе с тем важной формой закона больших чисел является теорема Чебышева: При достаточно большом числе независимых опытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности к ее математическому ожиданию:
где m – математическое ожидание с.в., Теорема Чебышева может быть легко обобщена и на более сложный случай, а именно когда закон распределения случайной величины Х от опыта к опыту не остается одним и тем же, а изменяется. Тогда вместо среднего арифметического наблюденных значений одной и той же величины Х с постоянными математическим ожиданием и дисперсией мы имеем дело со средним арифметическим n различных случайных величин, с различными математическими ожиданиями и дисперсиями. В этом случае при соблюдении некоторых условий среднее арифметическое является устойчивым и сходится по вероятности к определенной неслучайной величине: Если Х1, Х2, …, Хn – независимые случайные величины с математическим ожиданиями m1, m2, …, mn и дисперсиями D1, D2, …, Dn и если дисперсии ограничены одним и тем же числом С, то при возрастании n среднее арифметическое наблюденных значений величин Х1, Х2, …, Хn сходится по вероятности к среднему арифметическому их математических ожиданий m1, m2, …, mn:
Сущность теоремы Чебышева состоит в том, что каковы бы не были случайные величины, которые могут принимать отдельные значения, далекие от своих математических ожиданий, среднее арифметическое большого числа случайных величин принимает значение среднего арифметического их математических ожиданий. Другими словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеяно мало. Из этого можно сделать заключение, что сумма достаточно большого числа случайных величин уже не является случайной величиной.
Задача. Для установления размера некоторого изделия произведено 100 независимых измерений. Точность каждого измерения, определяемая средним квадратическим отклонением, не превышает 0,05 мм. В качестве размера изделия берется среднее арифметическое результатов 100 измерений. Оценить вероятность того, что допускаемая погрешность не превышает 0,01 мм. Решение. Пусть m – истинный размер изделия, Хk – результат k -го замера изделия, k = 1, 2, …, n. Погрешность, допускаемая при замене истинного размера изделия m на среднее арифметическое результатов измерения, есть величина Полагая в формуле (33.2) Следствием из закона больших чисел является теорема Я. Бернулли, устанавливающая связь между частотой события и его вероятностью. Пусть производится n независимых опытов, в каждом из которых может появиться или не появиться некоторое событие А, вероятность которого в каждом опыте равна р. Теорема Бернулли утверждает, что При неограниченном увеличении числа опытов n частота события А сходится по вероятности к его вероятности р, т.е.
Теорема Бернулли утверждает устойчивость частоты при постоянных условиях опыта, позволяет при большом числе опытов в качестве приближенного значения вероятности события Р(А) взять его относительную частоту При изменяющихся условиях опыта аналогичная устойчивость также существует. Теорема, устанавливающая свойство устойчивости частот при переменных условиях опыта, называется теоремой Пуассона и формулируется так: Если производится n независимых опытов и вероятность появления события А в i-том опыте равна pi, то при увеличении n частота события А сходится по вероятности к среднему арифметическому вероятностей pi. Теорема Пуассона выводится из теоремы Чебышева, как и теорема Бернулли. Теорема Пуассона имеет большое принципиальное значение для практического применения теории вероятностей. В частности в области опытной проверки вероятностных расчетов. На практике очень часто встречается случай, когда требуется проверить на опыте соответствие вычисленной вероятности какого-либо события А его фактической частоте. Это делается для проверки правильности той или иной теоретической схемы, положенной в основу метода вычисления вероятности события. При такой экспериментальной проверке не удается воспроизвести достаточно много раз одни и те же условия опыта. Проверка же осуществляется путем сравнения наблюденной в опыте частоты события, но не с его вероятностью, а со средним арифметическим вероятностей, вычисленных при различных условиях.
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 808; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 , где
, где  , где а и b – параметры, подлежащие определению.
, где а и b – параметры, подлежащие определению. принимает наименьшее возможное значение, при этом
принимает наименьшее возможное значение, при этом 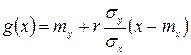 , где mx, my – математические ожидания, σx, σy - средние квадратические отклонения составляющих Х и Y соответственно, rxy – коэффициент корреляции.
, где mx, my – математические ожидания, σx, σy - средние квадратические отклонения составляющих Х и Y соответственно, rxy – коэффициент корреляции. называется прямой среднеквадратической регрессии Y на Х. Угловой коэффициент а функции
называется прямой среднеквадратической регрессии Y на Х. Угловой коэффициент а функции  , равный
, равный  , называется коэффициентом регрессии Y на Х.
, называется коэффициентом регрессии Y на Х.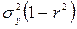 называется остаточной дисперсией случайной величины Y относительно случайной величины Х. Остаточная дисперсия характеризует величину ошибки, которую допускают при замене Y линейной функцией
называется остаточной дисперсией случайной величины Y относительно случайной величины Х. Остаточная дисперсия характеризует величину ошибки, которую допускают при замене Y линейной функцией  остаточная дисперсия равна нулю, т.е. при крайних значениях коэффициента корреляции не возникает ошибки при представлении Y в виде линейной функции от Х, т.е. другими словами при
остаточная дисперсия равна нулю, т.е. при крайних значениях коэффициента корреляции не возникает ошибки при представлении Y в виде линейной функции от Х, т.е. другими словами при  , т.е. Y от Х не зависит.
, т.е. Y от Х не зависит. и остаточную дисперсию
и остаточную дисперсию 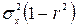 величины Х относительно величины Y.
величины Х относительно величины Y. ;
; .
. ;
; .
. , вероятность того, что величина Х отклонится от своего математического ожидания не меньше, чем на
, вероятность того, что величина Х отклонится от своего математического ожидания не меньше, чем на  :
: . (33.1)
. (33.1)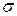 ».
». . С учетом того, что
. С учетом того, что  , имеем:
, имеем: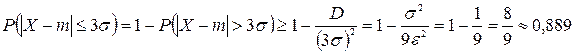 .
.
 .
. ,
,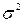 – дисперсия.
– дисперсия. . (33.2)
. (33.2) . По условию
. По условию  , значит
, значит  .
. ,
,  ,
,  , получаем искомую оценку вероятности:
, получаем искомую оценку вероятности: 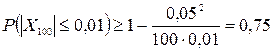 .
. .
. .
.


