
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следствия из теоремы сложения вероятностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Если события А1, А2, …, Аn образуют полную группу случайных событий, то сумма их вероятностей равна 1, т.е. В самом деле, так как А1, А2, …, Аn образуют полную группу случайных событий, то появление хотя бы одного из них – достоверное событие: Р(А1+ А2+ …+Аn)= 1. Так как А1, А2, …, Аn – несовместные события, то к ним применима теорема сложения вероятностей: Р(А1+ А2+ …+Аn)= Р(А1)+Р(А2)+ …+Р(Аn)=1, т.е. 2. Сумма вероятностей противоположных событий равна 1, т.е. Р(А)+Р( В самом деле, А и
Следствие 2 весьма важно в практическом применении теории вероятности. На практике часто оказывается легче вычислить вероятность противоположного события Задача. Круговая мишень состоит из трех зон: 1, 2, 3. Вероятность попадания в первую зону при одном выстреле 0,15, во вторую – 0,23, в третью – 0,17. Найти вероятность промаха. Решение. Обозначим А – промах,
В том случае, когда события А и В являются совместными, теорема сложения вероятности формулируется следующим образом.
Вероятность того, что в одном и том же опыте произойдет хотя бы одно из двух совместных событий, равна сумме вероятностей этих событий без вероятности их совместного появления, т.е. если А и В совместны, то Р(А+В)=Р(А)+Р(В)-Р(АВ).
В самом деле, А+В=АВ+А Р(А)=Р( АВ+А Имеем: Р(А Формула доказана.
Аналогично вероятность суммы трех совместных событий вычисляется по формуле Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(АВ)-Р(АС)-Р(ВС)+Р(АВС). Для произведения событий можно записать следующую формулу: Р(АВ)=Р(А)+Р(В)-Р(А+В). Задача. Техническое устройство состоит из трех агрегатов: двух агрегатов первого типа - А 1 и А 2, и одного агрегата второго типа В. Агрегаты А 1 и А 2 дублируют друг друга: при отказе одного из них происходит автоматическое переключение на второй. Агрегат В не дублирован. Для того чтобы устройство прекратило работу (отказало), нужно, чтобы одновременно отказали оба агрегата А 1 и А 2 или же агрегат В. Таким образом, отказ устройства - событие С – представляется в виде: С = А 1 А 2 +В, где А 1 и А 2 - соответственно отказ агрегатов А 1 и А 2, В – отказ агрегата В. Требуется выразить вероятность события С через вероятность событий, содержащих только суммы, а не произведения событий А 1, А 2 и В. Решение. Р(С)=Р(А1 А2 +В)=Р(А1 А2)+Р(В)-Р(А1 А2 В); Р(А1 А2)= Р(А1)+Р(А2)-Р(А1 + А2). Аналогично Р(А1 А2 В)= Р(А1)+Р(А2)+Р(В)-Р(А1 + А2)- Р(В + А2)- Р(А1 + В)+ Р(А1 +А2 +В). Подставляя эти выражения в первоначальное равенство, получим Р(С)= Р(В + А2)+ Р(А1 + В)- Р(А1 +А2 +В).
Теорема умножения вероятностей Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло ли событие В или нет. Примеры зависимых и независимых событий 1. А – «появление герба при первом подбрасывании монеты»; В – «появление герба при втором подбрасывании монеты». А и В – независимые события. 2. В урне два белых шара и один черный. Два лица вынимают по одному шару; рассматриваются события: А – «появление белого шара у первого лица»; В – «появление белого шара у второго лица». Вероятность события А равна 2/3, после того, как событие А произошло, вероятность события В равна ½. Событие А зависит от события В.
Вероятность события А, вычисленная при условии, что имело место событие В, называется условной вероятностью события А и обозначается: РВ(А). Очевидно, что условие независимости событий А и В имеет вид: Р(А)=РВ(А).
Теорема умножения вероятности формулируется следующим образом. Вероятность одновременного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место, т.е. Р(АВ)=Р(А)РА(В). Докажем теорему. Рассмотрим события А и В и противоположные им
Имеем: Р(АВ)= Следствие из теоремы умножения вероятностей:
Т еорема умножения вероятностей независимых событий формулируется следующим образом: Вероятность одновременного появления двух независимых событий равна произведению вероятностей этих событий, т.е. Р(АВ)=Р(А)Р(В). Задачи. 1. В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара. Найти вероятность того, что оба шара белые. 2. Та же задача при условии, что после первого вынимания шар возвращается в урну, и шары в урне перемешиваются. Решение. 1. А – появление двух белых шаров, В – появление первого белого шара, С – появление второго белого шара. Р(С)=Р(А)РА(В)=(2/5)(1/4)=0,1. 2. Р(С)=Р(А)Р(В)=(2/5)(2/5)=0,16 Р(С)=Р(А)РА(В)=(2/5)(1/4)=0,1.
Контрольные вопросы
1. Что называется суммой а) двух событий? б) трех событий? 2. Что называется произведением а) двух событий? б) трех событий? 3. Что называется разностью двух событий? 4. Какими свойствами обладают операции над событиями? 5. Как определяются а) зависимые события? б) независимые события? 6. Как определяется условная вероятность? 7. Как определить вероятность появления хотя бы одного из двух несовместных случайных событий А и В? 8. Как определить вероятность появления хотя бы одного из двух совместных случайных событий А и В? 9. Как определить вероятность одновременного появления двух независимых случайных событий А и В? 10. Как определить вероятность одновременного появления двух зависимых случайных событий А и В? 11. Как можно сформулировать условие независимости двух событий?
Контрольные задания
1. Доказать законы двойственности. 2. Доказать, что вероятность появления хотя бы одного из событий А, В, С удовлетворяет соотношению Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(АВ)-Р(АС)-Р(ВС)+Р(АВС). 3. В лотерее разыгрывается 100 билетов. Выигрыш падает на 10 билетов. Какова вероятность того, что хотя бы один из них выиграет? 4. Определить вероятность того, что случайно взятое двузначное число окажется кратным 2 или 9, или тому и другому одновременно. 5. На 30 одинаковых жетонах написаны 30 двузначных чисел от 1 до 30. Жетоны помещены в пакет и тщательно перемешаны. Какова вероятность вынуть жетон с номером, кратным 2 или 3? 6. В урне 6 голубых и 4 красных шара. Из нее извлекаются подряд два шара. Какова вероятность того, что а) оба шара голубые? б) один шар голубой, а второй – красный? 7. Известно, что Р(А)=0,7, Р(В)=0,3, Р(С)=0,1. Найти вероятность того, что в опыте, связанном с появлением этих событий трех событий, произойдет а) только одно из них; б) хотя бы одно из них; в) не менее двух из них; г) только два из них. 8. В мастерской работают два мотора, независимо друг от друга. Вероятность того, что в течение часа первый мотор не потребует внимания мастера, равна 0,85, а для второго мотора эта вероятность равна 0,8. Найти вероятность того, что в течение часа а) хотя бы один из моторов потребует внимания мастера; б) ни один из моторов не потребует внимания мастера.
Формула полной вероятности Следствием обеих основных теоремы – теоремы сложения и теоремы умножения вероятности – является формула полной вероятности. Допустим, что некоторое событие А может произойти вместе с одним из событий Н1, Н2, …, Нn, образующих полную группу случайных событий. Поскольку заранее неизвестно, с каким именно из Н1, Н2, …, Нn произойдёт событие А, то Н1, Н2, …, Нn называются гипотезами. Вероятность события А в этом случае вычисляется по формуле полной вероятности
В с.д., так как гипотезы Н 1, Н 2, …, Нn образуют полную группу, то событие А может появиться только в комбинации с какой-либо из гипотез: А=АН1+А Н2+ …+А Нn. Так как гипотезы Н1, Н2, …, Нn несовместны, то и комбинации АН1, АН2, …, АНn также несовместны; применяя к ним теорему сложения, получим:
Применяя к событиям АН 1, АН 2, …, АН n теорему умножения, получим:
Задача. Имеются три одинаковые на вид урны; в первой урне два белых и один чёрный шар; во второй – три белых и один чёрный; в третьей – два белых и два чёрных шара. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что этот шар белый. Решение. Рассмотрим событие А – «появление белого шара» и три гипотезы: Н1 – «выбор первой урны»; Н2 – «выбор второй урны»; Н3 – «выбор третьей урны». По условию задачи гипотезы равновозможны, т.е.
8. Теорема гипотез (формула Бейеса)
Следствием теоремы умножения вероятности и формулы полной вероятности является так называемая теорема гипотез или формула Бейеса. Допустим, что имеется полная группа неизвестных гипотез Н1, Н2, …, Нn. Вероятности этих гипотез до опыта известны и равны соответственно Р(Н1), Р(Н2), …, Р(Нn). Произведен опыт, в результате которого появилось событие А. Спрашивается, как следует изменить вероятности гипотез в связи с появлением этого события? Найти условную вероятность
В с.д., из теоремы умножения имеем:
Приравнивая правые части, имеем:
Выражая Р(А) с помощью формулы полной вероятности, имеем
Задача. Два стрелка независимо друг от друга стреляют по одной и той же мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку. Решение. Обозначим событие А – «в мишени обнаружена пробоина». До опыта возможны следующие гипотезы: Н1 – «ни первый, ни второй стрелок не попадают»; Н2 – «оба стрелка попадут»; Н3 – «первый стрелок попадёт, а второй не попадёт»; Н4 – «первый стрелок не попадёт, а второй попадёт». Вероятности гипотез:
Условные вероятности события А при этих гипотезах соответственно равны:
После опыта гипотезы Н1 и Н2 становятся невозможны, а вероятности гипотез Н3 и Н4 будут равны:
Контрольные вопросы
1. Что называют гипотезами? 2. Какому условию должны удовлетворять вероятности гипотез? 3. Как выглядит формула полной вероятности? 4. При каком условии применяется формула полной вероятности? 5. Как выглядит формула Бейеса? 6. При каких условиях применяется формула Бейеса?
Контрольные задания 1. Предположим, что 5% всех мужчин и 0,25% всех женщин страдают дальтонизмом. Наугад выбранное лицо является дальтоником. Какова вероятность, что это мужчина (считать, что мужчин и женщин одинаковое количество). 2. В цехе работает 20 станков. Из ни 10 марки А, 6 – марки В, 4 – марки С. Вероятность, что качество детали окажется отличным для станков А, В и С соответственно равна 0,9, 0,8 и 0,7. Какой процент отличных деталей выпускает цех в целом? 3. Однотипные приборы выпускаются тремя заводами в количественном соотношении1:2:3, причем вероятности брака для этих заводов соответственно равны 3%, 2%, 1%. Прибор, приобретенный НИИ, оказался бракованным. Какова вероятность того, что этот прибор изготовлен первым заводом? 4. Партия транзисторов, среди которых 10% дефектных, поступает на проверку. Схема проверки такова, что с вероятностью 0,95 обнаруживает дефект, если он есть, и существует нулевая вероятность того, что исправный транзистор будет признан дефектным. Случайно выбранный транзистор был признан дефектным. Какова вероятность того, что на самом деле транзистор исправен? 5. Имеется три урны с шарами. В первой находится 5 голубых и 3 красных шара, во второй – 4 голубых и 4 красных шара, а в третьей – 8 голубых. Наугад выбирается урна и из нее наугад выбирается шар. Найти вероятность того, что шар окажется красным. 6. В пяти ящиках лежат одинаковые по размерам и весу шары. В двух ящиках – по 6 голубых и 4 красных шара. В двух других ящиках – по 8 голубых и 2 красных шара. В одном ящике – 2 голубых и 8 красных шаров. Наудачу выбирается ящик и из него извлекается шар. Какова вероятность того, что извлеченный шар оказался голубым? 7. В мае вероятность дождливого дня равна 0,2. Для некоторой футбольной команды вероятность выиграть в ясный день равна 0,7, но зато в дождливый день эта вероятность равна лишь 0,4. Известно, что команда выиграла матч. Какова вероятность того, что в этот день шел дождь? 8. Из 100 студентов, пришедших на экзамен, 80 подготовились к экзамену, а 20 нет. Вероятность того, что подготовленный студент сдаст экзамен, равна 0,9. Аналогичная вероятность для неподготовленного студента равна 0,05. Наудачу выбранный студент сдал экзамен. Какова вероятность того, что он был подготовлен к экзамену? 9. Из партии, в которой 5 изделий, извлечено одно бракованное изделие. Считая равновозможными все предположения о первоначальном составе партии, найти вероятность того, что в партии первоначально было именно а) одно бракованное изделие; б) три бракованных изделия.
Литература 1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2002. – Гл. 1 – 4. 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2002. – Гл. 1 – 2. 3. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1999– Гл. 1 – 3.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1077; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.89.197 (0.012 с.) |

 .
. .
. )=1.
)=1.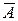 образуют полную группу случайных событий, значит в соответствии со свойством 1 имеем: Р(А)+Р (
образуют полную группу случайных событий, значит в соответствии со свойством 1 имеем: Р(А)+Р ( ).
).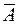 - попадание, тогда
- попадание, тогда  , где
, где  – попадание в i -тую зону. Р (
– попадание в i -тую зону. Р ( +
+  )+Р(
)+Р( . Пусть при n испытаниях событию АВ благоприятствует k случаев, А
. Пусть при n испытаниях событию АВ благоприятствует k случаев, А  , Р(А)=
, Р(А)=  , РА(В)=
, РА(В)=  . Выполняется тождество: Р(АВ)=Р(А)РА(В).
. Выполняется тождество: Р(АВ)=Р(А)РА(В). , следовательно
, следовательно  , т.е. отношение безусловных вероятностей равно отношению условных вероятностей.
, т.е. отношение безусловных вероятностей равно отношению условных вероятностей.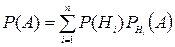 .
. .
. . Условные вероятности события А при этих гипотезах соответственно равны:
. Условные вероятности события А при этих гипотезах соответственно равны: ,
,  ,
,  . По формуле полной вероятности имеем:
. По формуле полной вероятности имеем: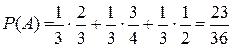 .
. позволяет формула Бейеса (теорема гипотез):
позволяет формула Бейеса (теорема гипотез): .
.
 .
. , откуда
, откуда
 ;
;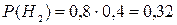 ;
; ;
;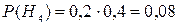 .
. ,
,  ,
,  ,
,  .
. ;
;  .
.


