
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория вероятностей и элементы математической статистикиСодержание книги
Поиск на нашем сайте
Типовой расчет №9 ТЕОРИЯ ВЕРОЯТНОСТЕЙ И ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Вариант 1. Классическое определение вероятности. Среди 18 деталей 6 изготовлены первым заводом, 4 – вторым, 8 – третьим заводами. а) найти вероятность того, что среди взятых наугад пяти деталей 2 изготовлены первым, 2 - вторым и 1 - третьим заводами; б) какова вероятность того, что среди пяти деталей окажется не меньше четырех деталей первого завода?
Теоремы сложения и умножения вероятностей. Три стрелка стреляют по цели. Вероятность попасть в цель для первого стрелка 0,75, для второго - 0,8, для третьего - 0,9. а) какова вероятность того, что в цель попадут ровно 2 стрелка? б) найти вероятность того, что в цель попадет хотя бы 1 стрелок.
Формула полной вероятности и формула Байеса. Известно, что из 100 деталей 60 изготовлены первым заводом, 40 - вторым. На первом заводе 5% изделия бракованные, на втором - 3%. а) найти вероятность того, что наудачу взятая деталь окажется бракованной; б) взята бракованная деталь. какова вероятность того, что она изготовлена первым заводом?
Схема Бернулли. Предельные теоремы в схеме Бернулли. Вероятность того, что деталь бракованная, равна 0,2. а) какова вероятность того, что из 7 деталей 2 бракованные? б) какова вероятность того, что из 100 деталей 22 бракованные? в) какова вероятность того, что из 100 деталей бракованных больше 20?
Дискретные случайные величины. Закон распределения дискретной случайной величины имеет вид:
Вычислить:
Непрерывные случайные величины. Плотность распределения непрерывной случайной величины
Вычислить: параметр
Нормальное распределение. Диаметр валика является нормально распределенной случайной величиной с проектным диаметром (средним значением) 25 мм и дисперсией 4 мм 2. Найти: а) вероятность того, что диаметр будет больше 25 мм, но меньше 27 мм; б) диаметр валика будет отличаться вот проектного не больше, чем на 2 мм.
Обработка статистических данных По заданным выборочным значениям признака Х 1) составить вариационный ряд; 2) вычислить относительные частоты; 3) построить полигон частот; 4) найти эмпирическую функцию распределения и построить ее график; 5) вычислить числовые характеристики выборки: среднее выборочное значение
Уравнение линейной регрессии По заданным выборочным значениям пары признаков Х, У 1) построить корреляционное поле для двумерной выборки; 2) найти коэффициент корреляции между Х и У и сделать вывод о связи признаков Х и У; 3) составить уравнение линейной регрессии У на Х и нанести линию регрессии на корреляционное поле.
Утверждено на заседании кафедры ВПМиИ Протокол №___ от _____________г.
Заведующий кафедры проф. Левин В.М. Донбасская национальная академия строительства и архитектуры
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 ТЕОРИЯ ВЕРОЯТНОСТЕЙ И ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Вариант 2.
Классическое определение вероятности. На предприятии работают 8 мужчин и 3 женщины. В профсоюзе есть 3 путевки, которые разыгрываются жребием. Найти вероятность: а) все путевки получат женщины; б) все путевки получат мужчины; в) путевку получит хотя бы один мужчина.
Теоремы сложения и умножения вероятностей. Бензин есть на первой заправке с вероятностью 0,6; на второй с вероятностью 0,3; на третьей - 0,7. Найти вероятности: а) бензин есть ровно на двух заправках; б) бензин отсутствует на всех заправках; в) бензин есть хотя бы на одной заправке.
Формула полной вероятности и формула Байеса. Есть две коробки с конфетами: в 1-й 20 шоколадных и 5 карамелек, в 2-й 10 шоколадных и 20 карамелек. Найти вероятность: а) будет вынута шоколадная конфета; б) вынута карамелька. Какова вероятность, что она из первой коробки?
Схема Бернулли. Предельные теоремы в схеме Бернулли. Вероятность того, что контролер ВТК выявит брак изделия ровная 0,15. Найти вероятность: а) бракованными признаны 2 изделия из 8. б) среди 80 изделий брак выявлен в 20 изделиях; в) среди 80 изделий бракованных выявлено менее 20.
Нормальное распределение. Вес изделия является случайной величиной, которая имеет нормальное распределение со средним значением 106 кг и дисперсией 9 кг2. Найти вероятность того, что: а) вес изделия находится в пределах от 100 до 110 кг. б) вес изделия отличается от среднего не более чем на 2 кг.
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 3.
Нормальное распределение. Плотность распределения случайной величины имеет вид:
Найти: Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 4.
Нормальное распределение. Случайная величина
Найти: Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 5.
Нормальное распределение. Случайная величина распределена нормально Найти вероятности: Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 6.
Нормальное распределение. Случайная величина распределена нормально с параметрами Найти вероятности: а) б) Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 7.
Нормальное распределение. Случайная величина имеет плотность распределения:
Найти:
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 8. Нормальное распределение. Плотность распределения случайной величины
Найти: Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 9.
Нормальное распределение. Размер детали является случайной величиной, которая имеет нормальное распределение с средним значением 120 мм и дисперсией 4 мм. Найти вероятность того, что: а) размер детали находится в пределах вот 118 мм и 121 мм; б) размер детали отличается от среднего не более чем на 1 мм.
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 10.
Нормальное распределение. Случайная величина а) б) Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 11.
Две работницы изготовили одинаковый комплект деталей. Вероятность, что первая работница допустила ошибку, равна 0,05, для второй эта вероятность равна 0,1. Обнаружена ошибка. Найти вероятность того, что ошиблась первая работница?
Нормальное распределение. Функция распределения случайной величины
Найти: Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 12.
Нормальное распределение. Случайная величина а) Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 13.
Нормальное распределение. Вес изделия представляет собой случае величину, имеющую нормальное распределение со средним значением 900 г и средним квадратическим отклонением 10 г. Найти вероятность того, что: а) вес изделия находится в пределах от 880 до 910г.; б) вес изделия отличается от среднего не более чем на 5 г.
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 14.
Нормальное распределение. Случайная величина а) Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 15.
Нормальное распределение. Случайная величина а) б) Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 16. Нормальное распределение. Диаметр валика оказывается нормально распределенной случайной величиной с проектным диаметром (средним значением) 25 мм и дисперсией 4 мм 2. Найти: а) вероятность того, что диаметр будет больше 25 мм, но меньше 27 мм. б) диаметр валика будет отличаться от проектного не более чем на 2 мм.
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 17.
Нормальное распределение. Вес изделия оказывается случайной величиной, какова имеет нормальное распределение со средним значением 106 кг и дисперсией 9 кг2. Найти вероятность того, что: а) вес изделия находится в пределе от 100 до 110 кг. б) вес изделия отличается от среднего не более чем на 2 кг.
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 18.
Нормальное распределение. Плотность распределения случайной величины имеет вид:
Найти: Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 19.
Нормальное распределение. Случайная величина имеет плотность распределения:
Найти: Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 20.
Нормальное распределение. Случайная величина распределена нормально найти вероятности:
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 21.
Нормальное распределение. Случайная величина распределена нормально найти вероятности: а) б)
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 22.
Нормальное распределение. Случайная величина имеет плотность распределения:
Найти:
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 23. Нормальное распределение. Плотность распределения случайной величины
Найти: Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 24.
Нормальное распределение. Размер детали является случайной величиной, которая имеет нормальное распределение со средним значением 120 мм и дисперсией 4 мм. Найти вероятность того, что: а) размер детали находится в пределах от 118мм до 121 мм; б) размер детали отличается от среднего не более чем на 1 мм.
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 25.
Нормальное распределение. Случайная величина а) б)
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 26.
Две работницы выполнили одинаковый объем работы. Вероятность, что первая допустила ошибку, равняется 0,05, для второй эта вероятность равняется 0,15. Выявлена ошибка. Найти вероятность того, что ошиблась первая работница.
Нормальное распределение. Функция распределения случайной величины
Найти: Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 27.
Нормальное распределение. Случайная величина а) Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 28.
Нормальное распределение. Вес изделия представляет собой случайную величину, имеющую нормальное распределение со средним значением 900 г и средним квадратическим отклонением 10 г. Найти вероятности, что: а) вес изделия находится в пределах от 880 до 910 г.; б) вес изделия отличается от среднего не более, чем на 5 г.
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 29.
Нормальное распределение. Случайная величина а) Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 Вариант 30.
Нормальное распределение. Случайная величина а) б) Типовой расчет №9 ТЕОРИЯ ВЕРОЯТНОСТЕЙ И ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Вариант 1.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 558; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.85 (0.009 с.) |


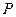

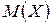 ,
,  ,
,  ,
,  ,
,  .
. имеет вид:
имеет вид:

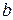 ,
,  .
.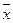 , исправленную выборочную дисперсию
, исправленную выборочную дисперсию  , исправленное среднее квадратическое отклонение
, исправленное среднее квадратическое отклонение  , моду Мо и медиану Ме.
, моду Мо и медиану Ме.
 ,
,  ,
,  .
. имеет плотность распределения:
имеет плотность распределения:
 ,
, 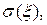 ,
,  ,
,  .
. ,
, 
 ,
,  .
. ,
,  .
. ,
, .
.
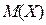 ,
,  ,
,  ,
,  .
. имеет вид:
имеет вид:
 ,
,  ,
,  .
. ,
,  . Найти вероятность того, что:
. Найти вероятность того, что: ;
; .
.
 ,
,  .
.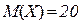 ,
, 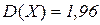 . найти:
. найти: ; б)
; б)  .
. ; б)
; б)  .
.


