
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Три стрелка стреляют по цели. Вероятность попасть в цель для первого стрелка 0,75, для второго - 0,8, для третьего - 0,9.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
а) какова вероятность того, что в цель попадут ровно 2 стрелка? б) найти вероятность того, что в цель попадет хотя бы 1 стрелок.
Формула полной вероятности и формула Байеса. Известно, что из 100 деталей 60 изготовлены первым заводом, 40 – вторым. На первом заводе на 5% изделий бракованных, на втором - 3%. а) найти вероятность того, что наугад взятая деталь окажется бракованной; б) взята бракованная деталь. Какова вероятность того, что она изготовлена первым заводом?
Схема Бернулли. Предельные теоремы в схеме Бернулли. Вероятность того, что деталь бракованная, равна 0,2. а) какова вероятность того, что с 7 деталей 2 бракованные? б) какова вероятность того, что из 100 деталей 22 бракованных? в) какова вероятность того, что из 100 деталей бракованных больше 20?
Дискретные случайные величины. Закон распределения дискретной случайной величины имеет вид:
Вычислить:
Непрерывные случайные величины. Плотность распределения непрерывной случайной величины
Вычислить: параметр
Нормальное распределение. Диаметр валика оказывается нормально распределенной случайной величиной с проектным диаметром (средним значением) 25 мм и дисперсией 4 мм 2. Найти: а) вероятность того, что диаметр будет больше 25 мм, но меньше 27 мм. б) диаметр валика будет отличаться от проектного не более чем на 2 мм.
Обработка статистических данных По заданным выборочным значениям признака Х 1) составить вариационный ряд; 2) вычислить относительные частоты; 3) построить полигон частот; 4) найти эмпирическую функцию распределения и построить ее график; 5) вычислить числовые характеристики выборки: среднее выборочное значение
Уравнение линейной регрессии По заданным выборочным значениям пары признаков Х, У 1) построить корреляционное поле для двумерной выборки; 2) найти коэффициент корреляции между Х и У и сделать вывод о связи признаков Х и У; 3) составить уравнение линейной регрессии У на Х и нанести линию регрессии на корреляционное поле.
Утверждено на заседании кафедры ВПМиИ Протокол №___ от _____________г.
Заведующий кафедры проф. Левин В.М.
Донбасская национальная академия строительства и архитектуры
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 ТЕОРИЯ ВЕРОЯТНОСТЕЙ И ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Вариант 17.
Классическое определение вероятности. На строительстве работают 8 мужчин и 3 женщины. В профсоюзе есть 3 путевки, которые разыгрываются жеребьевкой. Найти вероятность: а) все путевки получат женщины; б) все путевки получат мужчины; в) путевку получит хотя бы один мужчина.
Теоремы сложения и умножения вероятностей. Бензин есть на первой заправке с вероятностью 0,6; второй с вероятностью 0,8; на третьей – 0,7. найти вероятности: а) бензин есть ровно на двух колонках; б) бензин отсутствует на всех колонках; в) бензин есть хотя бы на одной колонке.
Формула полной вероятности и формула Байеса. Есть две коробки с конфетами: в 1-й 20 шоколадных и 5 карамелек, в 2-и 10 шоколадных и 20 карамелек. Найти вероятность: а) будет вынута шоколадная конфета; б) вынута карамелька. Какова вероятность, что она из 1-й коробки?
Схема Бернулли. Предельные теоремы в схеме Бернулли. Вероятность того, что деталь контролер ОТК обнаружит недостаток изделия, равна 0,15. Найти вероятность: а) признаны бракованными 2 изделия из 8. б) среди 80 изделий брак обнаружен в 20 изделиях; в) среди 80 бракованных изделий обнаружено менее 20.
Дискретные случайные величины. Закон распределения дискретной случайной величины имеет вид:
Вычислить:
Непрерывные случайные величины. Плотность распределения непрерывной случайной величины
Вычислить: параметр
Нормальное распределение. Вес изделия оказывается случайной величиной, какова имеет нормальное распределение со средним значением 106 кг и дисперсией 9 кг2. Найти вероятность того, что: а) вес изделия находится в пределе от 100 до 110 кг. б) вес изделия отличается от среднего не более чем на 2 кг.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.221.171 (0.008 с.) |


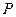

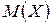 ,
,  ,
,  ,
,  ,
,  .
. имеет вид:
имеет вид:

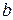 ,
,  .
.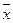 , исправленную выборочную дисперсию
, исправленную выборочную дисперсию  , исправленное среднее квадратическое отклонение
, исправленное среднее квадратическое отклонение  , моду Мо и медиану Ме.
, моду Мо и медиану Ме.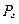
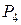 ,
, 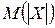 ,
, 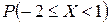 ,
, 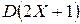 ,
, 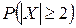 .
.
 .
.


