
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4: Полная вероятность и формулы БайесаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1. В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 6 черных шаров. Из наудачу взятой урны вынули один шар, который оказался черным. Тогда вероятность того, что этот шар вынули из второй урны, равна …
Решение:
2. Банк выдает 40% всех кредитов юридическим лицам, а 60% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,1; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило физическое лицо, равна …
0,07 0,05 Решение:
3. Банк выдает 35% всех кредитов юридическим лицам, а 65% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,15; а для физического лица эта вероятность составляет 0,1. Тогда вероятность непогашения в срок очередного кредита равна … 0,1175 0,125 0,8825 0,1275 Решение:
Тема 5: Законы распределения вероятностей одномерных дискретных случайных величин 1. Дискретная случайная величина
Решение:
2. Дискретная случайная величина
Решение:
3. Дискретная случайная величина Тогда вероятность
Решение:
Тема 6: Функция распределения вероятностей дискретной случайной величины 1. Дискретная случайная величина
Решение:
2. Для дискретной случайной величины 0,7 0,85 0,6 Решение:
3. Дискретная случайная величина
Решение:
4. Для дискретной случайной величины 0,655 0,25 0,45 Решение:
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 682; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |





 . Здесь
. Здесь 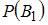 – вероятность того, что шар извлечен из первой урны;
– вероятность того, что шар извлечен из первой урны;  – вероятность того, что шар извлечен из второй урны;
– вероятность того, что шар извлечен из второй урны;  – условная вероятность того, что вынутый шар черный, если он извлечен из первой урны;
– условная вероятность того, что вынутый шар черный, если он извлечен из первой урны;  – условная вероятность того, что вынутый шар черный, если он извлечен из второй урны.
– условная вероятность того, что вынутый шар черный, если он извлечен из второй урны.




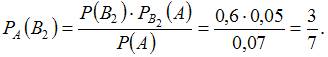

 задана законом распределения вероятностей:
задана законом распределения вероятностей: 
 равна …
равна …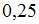






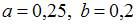
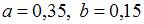

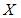 равна 1, то
равна 1, то  Этому условию удовлетворяет ответ:
Этому условию удовлетворяет ответ: 

 равна …
равна …









 ,
,  ,
, ,
,  ,
, ,
, 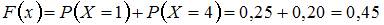 ,
, ,
,  .
.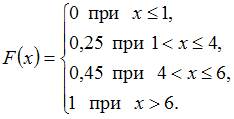

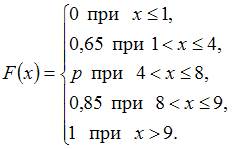
 может быть равно …
может быть равно … и
и  . Этим условиям удовлетворяет, например, значение
. Этим условиям удовлетворяет, например, значение  .
.




 . Тогда
. Тогда ,
,  ,
, ,
,  ,
,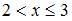 ,
,  ,
, ,
,  ,
, ,
,  .
.


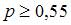 и
и  Этим условиям удовлетворяет, например, значение
Этим условиям удовлетворяет, например, значение  .
.


