
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 28: Эмпирическая функция распределения вероятностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1. Из генеральной совокупности
Решение:
2. Из генеральной совокупности
Решение:
3. Из генеральной совокупности
Решение:
5. Из генеральной совокупности
Решение: Тема 29: Основные понятия об оценках параметров распределения 1. Дан доверительный интервал 1,12 0,01 2,24 13,56 Решение:
3. Дан доверительный интервал
Решение:
4. Дан доверительный интервал
Решение:
Тема 30: Точечная оценка математического ожидания 1. Из генеральной совокупности извлечена выборка объема 13,14 13,0 13,34 13,2 Решение:
2. Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна … 6,38 6,42 6,1 6,4 Решение:
3. Из генеральной совокупности извлечена выборка объема
Решение: Тема 31: Точечная оценка дисперсии 1. Из генеральной совокупности извлечена выборка объема
Решение:
2. систематических ошибок) получены следующие результаты (в мм): 3,6; 3,8; 4,3. Тогда несмещенная оценка дисперсии равна … 0,13 0,065 3,9 0,7 Решение:
3. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна … 11,25 19,5 21,25 Решение:
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 855; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.44 (0.008 с.) |

 извлечена выборка объема
извлечена выборка объема  :
: ,
,





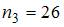


 где
где  – число вариант, меньших
– число вариант, меньших 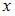 . Тогда при
. Тогда при  ,
, 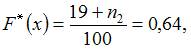 то есть
то есть 
 .
. имеет вид …
имеет вид …














 ,
,








 ,
,  то есть
то есть  .
. для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …
для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна … определяется как
определяется как  то есть
то есть 
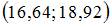 для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении объема выборки этот доверительный интервал может принять вид …
для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении объема выборки этот доверительный интервал может принять вид …

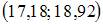

 , где точечная оценка математического ожидания
, где точечная оценка математического ожидания  , а точность оценки
, а точность оценки  . В случае увеличения объема выборки точность оценки улучшается, то есть значение
. В случае увеличения объема выборки точность оценки улучшается, то есть значение  будет меньше 1,14.
будет меньше 1,14. для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …
для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …



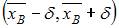 , где точечная оценка математического ожидания
, где точечная оценка математического ожидания  , а точность оценки
, а точность оценки  . В случае уменьшения надежности точность оценки улучшается, то есть значение
. В случае уменьшения надежности точность оценки улучшается, то есть значение  :
:
 То есть
То есть 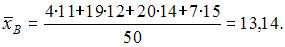
 То есть
То есть 
 :
:


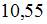


 :
:
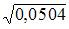



 , где
, где Тогда
Тогда
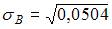 .
. где
где  Вычислив предварительно
Вычислив предварительно 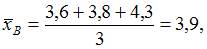 получаем
получаем
 где
где  получаем
получаем



