
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 24: Интегральная формула ЛапласаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Вероятность появления некоторого события в каждом из 400 независимых испытаний постоянна и равна 0,8. Тогда вероятность того, что событие появится не менее 300 и не более 328 раз, следует вычислять как …
Решение:
2. Вероятность появления некоторого события в каждом из 100 независимых испытаний постоянна и равна 0,2. Тогда вероятность того, что событие появится не менее 18 и не более 24 раз, следует вычислять как …
Решение:
3. Вероятность того, что деталь не пройдет проверку ОТК, равна 0,15. Тогда вероятность того, что среди 300 случайно отобранных деталей окажется не менее 50 деталей, не прошедших проверку ОТК, следует вычислить по … интегральной формуле Лапласа формуле полной вероятности формуле Пуассона локальной формуле Лапласа Решение:
Тема 25: Вариационный ряд 1. Статистическое распределение выборки имеет вид 0,25 0,05 0,26 0,75 Решение:
2. Из генеральной совокупности извлечена выборка объема Решение:
Тема 26: Полигон и гистограмма 1. Из генеральной совокупности извлечена выборка объема
Тогда относительная частота варианты 0,05 0,06 0,25 0,20 Решение:
2. Из генеральной совокупности извлечена выборка объема Тогда значение a равно … Решение:
3. Из генеральной совокупности извлечена выборка объема
Решение:
Тема 27: Характеристики вариационного ряда 1. Мода вариационного ряда 2, 4, 5, 7, 7, 7, 9, 9, 11, 12 равна … Решение:
2. Медиана вариационного ряда 11, 14, 16, 17, 17, 17, 18, 19, 21, 22, 22, 23, 25, 25 равна … 18,5 Решение:
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 788; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.204 (0.006 с.) |

 , где
, где 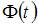 – функция Лапласа
– функция Лапласа , где
, где  , где
, где 
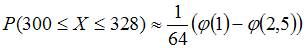 , где
, где  ) распределение, и это распределение является асимптотически нормальным. Это означает, что при больших значениях числа испытаний
) распределение, и это распределение является асимптотически нормальным. Это означает, что при больших значениях числа испытаний  расчет по формуле Бернулли
расчет по формуле Бернулли 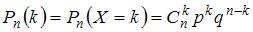 становится практически невозможным, особенно когда надо вычислять вероятности не отдельного равенства (события)
становится практически невозможным, особенно когда надо вычислять вероятности не отдельного равенства (события)  , а неравенств вида
, а неравенств вида 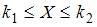 . Для вычисления таких вероятностей на практике используется интегральная формула Лапласа
. Для вычисления таких вероятностей на практике используется интегральная формула Лапласа  , где
, где 

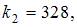
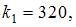

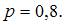

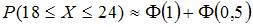 , где
, где 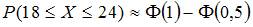 , где
, где 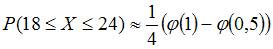 , где
, где  , где
, где 
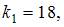


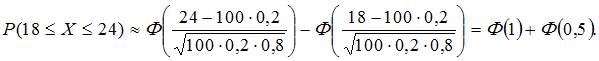


 равно …
равно …
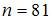 :
:
 равно …
равно … , где
, где  – частота варианты
– частота варианты  . Тогда
. Тогда 
 , полигон частот которой имеет вид:
, полигон частот которой имеет вид:
 в выборке равна …
в выборке равна … вычисляется по формуле
вычисляется по формуле  , где
, где  – объем выборки. Вычислим предварительно частоту варианты
– объем выборки. Вычислим предварительно частоту варианты 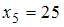 как
как  Тогда
Тогда 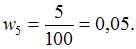
 , гистограмма частот которой имеет вид:
, гистограмма частот которой имеет вид:
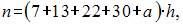 где
где 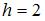 , то
, то 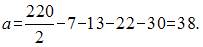
 , гистограмма относительных частот которой имеет вид
, гистограмма относительных частот которой имеет вид




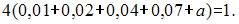 Тогда
Тогда  .
.


