
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последовательности независимых испытаний. ФормулыСодержание книги Поиск на нашем сайте
Бернулли, Лапласа, Пуассона Если производится несколько испытаний, таких, что вероятность рассматриваемого события A в каждом из испытаний не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события A. Испытаниями Бернулли называются повторные независимые испытания, в каждом из которых нас интересуют только два исхода (будем называть их «успех» и «неудача»), вероятности которых постоянны в каждом испытании. Например, при многократном подбрасывании монеты (за успех принимаем выпадение герба, за неудачу – выпадение решки) вероятность успеха p Если производится n независимых испытаний в одинаковых условиях, в каждом из которых с одной и той же вероятностью p может произойти событие A, то вероятность Pn (m) того, что в этих n испытаниях событие A произойдет ровно m раз, определяется по формулам Бернулли, Лапласа или Пуассона. 1 Обычно при решении задач формула Бернулли применяется, если число экспериментов невелико ( Формула Бернулли
где q = 1 – p – вероятность непоявления события A в каждом из испытаний;
2 Очевидно, что при больших значениях n пользоваться формулой Бернулли затруднительно, так как придется вычислять значения факториалов больших чисел и возводить в большую степень числа, близкие к нулю (0 < p < 1). В этом случае можно использовать асимптотические формулы Лапласа, дающие тем лучшее приближенное значение Pn (m) и Pn (k 1 £ m £ k 2), чем больше n.
Локальная теорема Лапласа. Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы (0 < p < 1), то вероятность того, что событие A появится в серии из n испытаний ровно m раз приближенно равна
где
(В приложении A приведена таблица значений функции Функция j(x) является четной функцией, то есть j(– x) = j(x), для всех
Интегральная теорема Лапласа. Если вероятность p наступления события A в каждом испытании постоянна и отлична от нуля и единицы (0 < p < 1), то вероятность того, что событие A появится в серии из n испытаний от k 1 до k 2 раз, приближенно равна
где
В приложении Б приведены таблицы значений функции Лапласа
Функция F(x) нечетна, то есть F(– x) = – F(x). При x > 5 можно принять F(x) = 0,5. 3 Пусть число экспериментов Бернулли велико (
Приведем таблицу, с помощью которой, можно определить формулу при решении задачи.
Таблица 1 – Условия применения формул при испытаниях Бернулли (цифры условные)
Наивероятнейшее число m 0 наступлений события A в серии из n испытаний, в каждом из которых оно может наступить с вероятностью p, определяется из двойного неравенства
np – q £ m 0 £ np + p. Пример 10 Предприятие для изучения потребительских предпочтений на товар в случайном порядке рассылает анкеты по а) какова вероятность того, что из б) найдите наиболее вероятное число анкет, «возвратившихся» на предприятие, и соответствующую этому значению вероятность. Рассмотрим решение задачи для трех вариантов:
Решение. Первый вариант. а) Для определения вероятности события В воспользуемся формулой Бернулли и теоремой сложения вероятностей несовместных событий:
Р(В) =
Р(В) =
б) Условие задачи можно рассматривать как серию из n = 10 независимых испытаний, состоящих в рассылке анкет, в каждом из которых с вероятностью
Определим наиболее вероятное число анкет, «возвратившихся» на предприятие по формуле np – q £ m 0 £ np + p. 3,4 £ m 0 £ 4,4.
Наивероятнейшее число m 0 = 4. Так как число испытаний невелико для вычисления вероятностей событий B = {из 10 разосланных анкет менее 4 «возвратились» на предприятие} и C = {из 10 разосланных анкет ровно 4 «возвратились» на предприятие} можно воспользоваться точной формулой Бернулли. Для определения вероятности события С воспользуемся формулой Бернулли
Решение. Второй вариант. а) Условие задачи можно рассматривать как серию из n = 100 независимых испытаний, состоящих в рассылке анкет, в каждом из которых с вероятностью Так как число испытаний достаточно велико для вычисления вероятностей событий B = {из 100 разосланных анкет менее 40 «возвратились» на предприятие} и C = {из 100 разосланных анкет ровно 40 «возвратились» на предприятие} можно воспользоваться приближёнными формулами Муавра-Лапласа: а) Для вычисления вероятности события B воспользуемся интегральной теоремой Муавра-Лапласа при n = 100; p = 0,4; q = 1 – 0,4 = 0,6; k 1 = 0; k 2 = 40:
По таблицам значений функции Таким образом,
б) Определим наиболее вероятное число анкет, «возвратившихся» на предприятие по формуле np – q £ m 0 £ np + p. 39,4 £ m 0 £ 40,4.
Наивероятнейшее число m 0 = 40. Для вычисления вероятности события С воспользуемся локальной теоремой Муавра-Лапласа. В данном случае n = 100; p = 0,4; q = 0,6; m = 40:
По таблицам значений функции
Ответ: а) вероятность того, что из 100 разосланных анкет не более 40 «возвратятся» на предприятие, равна 0,5; б) наиболее вероятное число разосланных анкет, «возвратившихся» на предприятие, составит 40, соответствующая этому числу вероятность 0,0814. Решение. Третий вариант. В данном случае для вычисления вероятностей воспользуемся приближенной формулой Пуассона с параметром a = np, так какчисло испытаний n = 200достаточно велико, а вероятность появления события в каждом испытании p = 0,05очень мала (p < 0,1), то есть в каждом отдельном опыте событие A появляется крайне редко:
Таблица значений функции a = np =
а) Определим событие В = {не более двух анкет «возвратятся» на предприятие, то есть или 0, или 1, или 2}.
Вероятность события В
б) Условие задачи можно рассматривать как серию из n = 200 независимых испытаний, состоящих в рассылке анкет, в каждом из которых с вероятностью Определим наиболее вероятное число анкет, «возвратившихся» на предприятие, по формуле np – q £ m 0 £ np + p, 9,05 £ m 0 £ 10,05.
Наивероятнейшее число m 0 = 10. Определим событие С = {10 анкет «возвратятся» на предприятие}. Вероятность события С
Ответ: а) вероятность того, что из 200 разосланных анкет не более 2 «возвратятся» на предприятие, равна 0,002769; б) наиболее вероятное число разосланных анкет, «возвратившихся» на предприятие, составит 10, соответствующая этому числу вероятность 0,12511.
Вопросы для самоконтроля
1 Какие испытания называются независимыми? Приведите примеры. 2 Какие испытания называются испытаниями Бернулли? Приведите примеры. 3 При каких условиях применяется формула Бернулли? 4 Что определяется по формуле Бернулли? 5 При каких условиях применяется предельная теорема Пуассона? 6 При каких условиях применяются предельные теоремы Myaвpa-Лапласа? 7 Что определяется по локальной теореме Муавра-Лапласа? 8 Что определяется по интегральной теореме Муавра-Лапласа? 9 Какое число называется наивероятнейшим числом наступлений события A в серии из n испытаний? СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.117.164 (0.013 с.) |

 , вероятность неудачи q = 1 – p
, вероятность неудачи q = 1 – p  , вероятность неудачи q = 1 – p
, вероятность неудачи q = 1 – p  .
. .
. , (10)
, (10) – число сочетаний из n элементов по m,
– число сочетаний из n элементов по m, , где
, где  .
.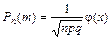 , (11)
, (11) .
.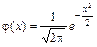 , соответствующих положительным значениям аргумента.)
, соответствующих положительным значениям аргумента.) принимается j(x) = 0.
принимается j(x) = 0. , (12)
, (12) ,
,  .
.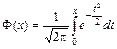 .
. ), а вероятность наступления события A в каждом испытании очень мала (
), а вероятность наступления события A в каждом испытании очень мала ( ), тогда вероятность того, что событие A появится в серии из n испытаний ровно m раз, приближенно равна
), тогда вероятность того, что событие A появится в серии из n испытаний ровно m раз, приближенно равна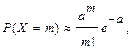 (13)
(13) где произведение
где произведение  .
.

 адресам (почтовый опрос). Вероятность того, что заполненные потребителями анкеты «возвратятся» на предприятие, составляет
адресам (почтовый опрос). Вероятность того, что заполненные потребителями анкеты «возвратятся» на предприятие, составляет  . Определить:
. Определить: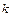 анкет;
анкет; +
+  +
+  +
+  ;
; ;
;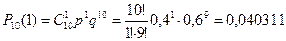 ;
; ;
; .
. может осуществиться событие A = {посланная анкета «возвратится» на предприятие}. Вероятность того, что посланная анкета «не возвратится» на предприятие, равна q = 1 – 0,4 = 0,6.
может осуществиться событие A = {посланная анкета «возвратится» на предприятие}. Вероятность того, что посланная анкета «не возвратится» на предприятие, равна q = 1 – 0,4 = 0,6. £ m 0 £
£ m 0 £ 
 .
. может осуществиться событие A = {посланная анкета «возвратится» на предприятие}. Вероятность того, что посланная анкета «не возвратится» на предприятие, равна q = 1 – 0,4 = 0,6.
может осуществиться событие A = {посланная анкета «возвратится» на предприятие}. Вероятность того, что посланная анкета «не возвратится» на предприятие, равна q = 1 – 0,4 = 0,6. ;
;

 находим F (–8,165) = = – 0,5, F (0) = 0,0.
находим F (–8,165) = = – 0,5, F (0) = 0,0. .
.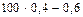 £ m 0 £
£ m 0 £ 
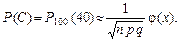

 находим j (0) = 0,3989.
находим j (0) = 0,3989.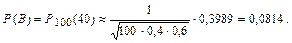

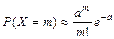 приведена в приложении В.
приведена в приложении В. .
.

 = 0,0028.
= 0,0028. может осуществиться событие A = {посланная анкета «возвратится» на предприятие}. Вероятность того, что посланная анкета «не возвратится» на предприятие, равна q = 1 – 0,05 = 0,95.
может осуществиться событие A = {посланная анкета «возвратится» на предприятие}. Вероятность того, что посланная анкета «не возвратится» на предприятие, равна q = 1 – 0,05 = 0,95.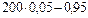 £ m 0 £
£ m 0 £ 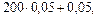

 .
.


