
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условная вероятность. Теорема умножения вероятностейСодержание книги Поиск на нашем сайте
Рассмотрим следующий вероятностный эксперимент Е. Пусть в пространстве Событие В называется зависимым от события А, если появление (или не появление) события А изменяет вероятность появления события В. Событие В называется независимым от события А, если появление (или не появление) события А не изменяет вероятность появления события В. Рассмотрим два произвольных события A и B, причем P (B) ¹ 0. Условной вероятностью события A при условии B (обозначается P (A | B)) называется вероятность события A, вычисленная при условии, что событие B произошло. По определению
P (A | B) = P (A Ç B)/ P (B). (4)
Вычисление условных вероятностей – это, по существу, переход в новое, урезанное заданным условием B пространство элементарных событий. Вероятности элементарных событий P (w i) (w i Î B) пропорциональны исходным. Для соблюдения условия нормировки в новом пространстве элементарных событий они делятся на P (B). Аналогично
P (B | A) = P (A Ç B)/ P (A) (5)
в случае, если P (A) ¹ 0. Формулы (2) и (3) часто записывают в виде
P (A Ç B) = P (B) P (A | B) = P (A) P (B | A) (6)
и называют теоремой умножения вероятностей. Для произвольного числа n событий A 1, A 2,… An теорема умножения вероятностей имеет вид
P (A 1 Ç A 2 Ç … Ç An) = P (A 1) P (A 2| A 1) … P (An | A 1 Ç A 2 Ç … Ç Аn -1),
то есть вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.
Пример 7 Студент пришел на зачет, зная из 30 вопросов только 20. Какова вероятность того, что он сдаст зачет, если для этого необходимо ответить хотя бы на два вопроса из трех, содержащихся в билете? Решение. Обозначим события: А = {студент сдаст зачет}; В = {студент ответит на три вопроса из трех, содержащихся в билете}; С = {студент ответит на два вопроса из трех, содержащихся в билете}.
События В и С несовместны. Событие А произойдет, если произойдет одно из событий В или С. По теореме сложения вероятностей несовместных событий P (А) = Определим вероятности событий В и С. В = {студент ответит на три вопроса из трех, содержащихся в билете}; В1 ={студент ответит на первый вопрос, содержащийся в билете}; В2 = {студент ответит на второй вопрос, содержащийся в билете}; В3 = {студент ответит на третий вопрос, содержащийся в билете}.
Вероятность события В определим по формуле
Р(В) = Р(В1) Р(В2 | В1) Р(В3 | В2 Ç В 1 ), где Р (В 1) = Р (В 2| В 1)= Р (В 3| В 2 Ç В 1) = По теореме умножения вероятностей зависимых событий P (В) = P (В 1) P (В 2| В 1) P (В 3| В 2Ç В 1) = Вероятность события С определим, используя теорему сложения вероятностей несовместных событий.
Р (С) = Р (С 1) + Р (С 2) + Р (С 3),
где С 1 = {студент отвечает на первый и второй вопросы, а на третий не отвечает}; С 2 = {студент отвечает на первый и третий вопросы, а на второй не отвечает}; С 3 = {студент отвечает на второй и третий вопросы, а на первый не отвечает}. P (С 1) = P (В 1) P (В 2| В 1) P ( = P (С 2) = P (В 1) P ( = P (С 3) = P ( = Р(С) = Р(С 1) + Р(С 2) + Р(С 3) = 0,156 + 0,156 +0,156 = 0,468. По теореме сложения вероятностей несовместных событий P (А) =
Независимые события Два события A и B называются независимыми, если
P (A Ç B) = P (A) P (B). (7)
Для пояснения естественности такого определения вернемся к теореме умножения вероятностей (6) и установим, в каких ситуациях из нее следует (7). Очевидно, что это может быть тогда, когда условная вероятность P (A | B) равна соответствующей безусловной вероятности события А: P (A | B) = P (A), то есть когда вероятность события А не зависит от того, произошло событие В или нет. (Аналогично, P (B | A) = P (B)). В основе независимости событий лежит их физическая независимость, состоящая в том, что множества факторов, влияющих на исход эксперимента и обусловливающих появление этих событий, не пересекаются или почти не пересекаются. События A 1, A 2,…, An называются независимыми в совокупности, если вероятность каждого из этих событий не зависит от появления любого числа остальных событий.
Теорема умножения вероятностей для независимых в совокупности событий A 1, A 2,…, An имеет вид
P (A 1 Ç A 2 Ç … Ç An) = P (A 1) P (A 2) … P (An).
Пример 8 При изготовлении изделие проходит три основные независимые операции. Вероятность получения стандартного изделия при первой операции равна 0,9, второй – 0,95, третьей – 0,8. Найти вероятность того, что: а) изделие окажется стандартным; б) изделие окажется нестандартным. Решение. Обозначим события: A i = { i -ю операцию изделие прошло без брака}, i = 1, 2, 3; B = {изделие окажется стандартным}; C = {изделие окажется нестандартным}. Согласно условию: вероятность события A 1 равна P (A 1) = 0,9, вероятность события A 2равна P (A 2) = 0,95, вероятность события A 3 равна P (A 3) = 0,8. Тогда вероятности противоположных событий:
Определим все события данного случайного эксперимента и соответствующие вероятности:
а) По теореме умножения вероятностей независимых событий
б) Применяя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, получим
События B = {изделие окажется стандартным} и C = {изделие окажется нестандартным} являются противоположными, то есть
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.63.107 (0.008 с.) |

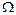 определены случайные события А, В, С, … и их вероятности. Предположим, что в ходе нашего эксперимента Е событие А уже произошло. В данном эксперименте появление события А может каким-то образом изменить вероятности появления событий, связанных (зависимых) с ним.
определены случайные события А, В, С, … и их вероятности. Предположим, что в ходе нашего эксперимента Е событие А уже произошло. В данном эксперименте появление события А может каким-то образом изменить вероятности появления событий, связанных (зависимых) с ним.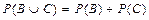 .
.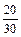 (всего 30 вопросов, из которых 20 студент знает);
(всего 30 вопросов, из которых 20 студент знает); (всего осталось 29 вопросов, из них 19 студент знает);
(всего осталось 29 вопросов, из них 19 студент знает); (всего осталось 28 вопросов, из них 18 студент знает).
(всего осталось 28 вопросов, из них 18 студент знает). =
=  = 0,281.
= 0,281.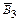 | В 2Ç В 1) =
| В 2Ç В 1) =  =
=  =
= = 0,156.
= 0,156. | В 1) P (В 3|
| В 1) P (В 3|  =
= 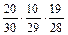 =
=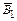 ) P (В 2|
) P (В 2|  =
= 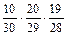 =
= ,
, ,
, .
.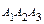




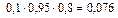











 .
.

 + +
+ +  +
+ 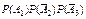
 +
+  = 0,036 + 0,076 + 0,171 + 0,004 + 0,009 + 0,019 + 0,001 = 0,316.
= 0,036 + 0,076 + 0,171 + 0,004 + 0,009 + 0,019 + 0,001 = 0,316. ,
,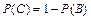 = 1 – 0,684= 0,316.
= 1 – 0,684= 0,316.


