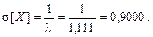Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормированное (стандартизованное) нормальное распределениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нормированным (или стандартизованным) нормальным распределением называется нормальное распределение с параметрами m = 0 и s = 1. Функция плотности распределения вероятностей стандартного распределения
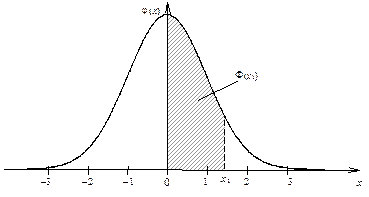
В приложении A приведены значения этой функции для неотрицательных значений аргумента, график функции j(x) изображен на рисунке 25.
Рисунок 25 – График функции j(x)
Вычислим для нормально распределенной случайной величины X вероятность попадания на участок от a до b:
Сделав в интеграле замену переменной t = (x – a)/s (то есть «нормируя» случайную величину) и, соответственно, изменяя пределы интегрирования, получим
Как известно, неопределенный интеграл
называемую функцией Лапласа (или «интегралом вероятностей»), для которой составлены таблицы значений. В геометрической интерпретации Ф(x) равна площади фигуры под кривой j(x), опирающейся на отрезок [0; x ]. На рисунке 23 это фигура выделена штриховкой. В приложении Б приведены значения функции Лапласа для положительных значений x. Функция F(x) – нечетная, то есть F(– x) = – F(x); при x > 5 можно принять F(x) = 0,5. С помощью функции Лапласа вероятность попадания нормально распределенной случайной величины X на участок от a до b выражается формулой
Формула для расчета вероятности отклонения нормально распределенной случайной величины Х от своего математического ожидания на величину
Примеры случайных величин, распределенных по нормальному закону. Известно, что нормально распределенные случайные величины широко распространены на практике. Нормальное распределение возникает в тех случаях, когда складывается большое число независимых (или слабо зависимых) случайных величин X 1, X 2, …, Xn:
причем эти величины сравнимы по порядку своего влияния на рассеивание суммы. Тогда, каковы бы ни были законы распределения отдельных величин Хi, закон распределения их суммы X будет близок к нормальному, причем тем ближе, чем больше число слагаемых n. На практике наиболее часто встречаются именно такие случайные величины. Результаты измерения длины, массы, времени, ошибки измерения и многие другие случайные величины имеют нормальное или близкое к нормальному распределение.
Пример 19 Случайная величина X распределена по нормальному закону с параметрами M [ X ] = m, s[ X ] = s. Найти вероятность того, что случайная величина X будет принимать значения, удаленные от математического ожидания не более чем на: а) s, б) 2s, в) 3s. Решение. Для вычисления искомых вероятностей воспользуемся формулой (27): а)
Произведем расчет, используя формулу (29):
где На рисунке 26 под графиком кривой нормального распределения указаны площади фигур, ограниченных кривой f (x) и осью абсцисс, которые равны вероятностям попадания значения случайной величины на указанные отрезки. График функции распределения F (x) изображен на рисунке 27.
Рисунок 26 – Вероятность того, что случайная величина X будет принимать значения, удаленные от математического ожидания не более чем на: а) s, б) 2s, в) 3s
Рисунок 27 – График функции распределения F (x)
б)
в)
Пример 20 Случайное отклонение изменения курса акций некоторой компании относительно их текущего курса является случайной величиной, распределенной по нормальному закону со средним квадратическим отклонением, равным 5 у.е. Систематические отклонения изменения курса акций от номинальной стоимости отсутствуют. Какова вероятность того, что в определенный день курс акции отклонится от номинала не более чем на 2 у. е.? Какова вероятность того, что в определенный день курс акции отклонится от номинала более чем на 2 у. е.? Решение. Рассмотрим случайную величину X – отклонение изменения курса акций некоторой компании относительно их текущего курса. Согласно условию, M [ X ] = 0 [у. е.], s[ X ] = 5 [у. е.]. Найдем вероятность события A ={в определенный день курс акции отклонится от номинала не более чем на 2 у. е.}:
Найдем вероятность события В = {в определенный день курс акции отклонится от номинала более чем на 2 у. е.}:
На рисунке 28 штриховкой выделена фигура, площадь которой равна вероятности события В.
Рисунок 28 – График плотности распределения вероятностей Таблица 2 – Некоторые виды законов распределения непрерывных законов распределения
Вопросы для самоконтроля
1 Какими параметрами определяется биномиальный закон распределения? 2 Какими параметрами определяется геометрический закон распределения? 3 Какими параметрами определяется закон Пуассона? 4 Приведите примеры случайных величин, распределенных по равномерному закону. 5 Какими параметрами определяется показательный закон распределения? 6 Какими параметрами определяется нормальный закон? 7 Как определяется вероятность попадания значения случайной величины, распределенной нормально, в некоторый интервал? 8 Чему равны мода, медиана, математическое ожидание случайной величины, распределенной по нормальному закону?
ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ ВАРИАНТ 1 Задача 1 При наборе телефонного номера абонент набирает 2 последние цифры наугад. Найти вероятность того, что номер будет набран правильно с первой попытки, если: а) абонент помнит, что цифры разные и нечетные; б) абонент помнит, что цифры нечетные. Задача 2 Два клиента зашли в магазин. Вероятность того, что первый клиент пожелает сделать покупку, равна 0,7, для второго клиента эта вероятность равна 0,5. Найти вероятность того, что захотят сделать покупку: а) оба клиента; б) только один клиент; в) хотя бы один клиент. Задача 3. Задан закон распределения дискретной случайной величины
Задача 4. Время пользования Интернетом в вечернее время распределено по показательному закону с математическим ожиданием, равным 0,9 часа. Найти вероятность того, что пользователь будет находиться в Интернете менее 1 часа. Найти среднее квадратическое отклонение времени пользования Интернетом. РЕШЕНИЕ ВАРИАНТА 1 Задача 1 При наборе телефонного номера абонент набирает 2 последние цифры наугад. Найти вероятность того, что номер будет набран правильно с первой попытки, если: а) абонент помнит, что цифры разные и нечетные; б) абонент помнит, что цифры нечетные. Решение. а) Элементарными исходами рассматриваемого эксперимента являются возможные варианты последовательного набора двух цифр из пяти. Так как в условии указано, что цифры нечетные и разные, то выбирать будем две цифры из 1, 3, 5, 7, 9. Пространство элементарных исходов рассматриваемого эксперимента: W = {(1, 3), (1, 5), (1, 7), (1, 9), (3, 1), (3, 5), (3, 7), (3, 9), (5, 1), (5, 3), (5, 7), (5, 9), (7, 1), (7, 3), (7, 5), (7, 9), (9, 1), (9, 3), (9, 5), (9, 7)}. В данном случае пространство элементарных исходов состоит из 20 элементов: n = 20. Поскольку цифры набираются случайным образом, все элементарные исходы равновозможны, то для вычисления вероятности интересующего нас события можно воспользоваться классическим методом определения вероятностей. Число исходов, благоприятных событию A, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
б) Элементарными исходами рассматриваемого эксперимента являются возможные варианты последовательного набора двух цифр из пяти. Так как в условии указано, что цифры нечетные, то выбирать будем две цифры из 1, 3, 5, 7, 9, с учетом того, что цифры могут повторяться. Пространство элементарных исходов рассматриваемого эксперимента: W = {(1, 1), (1, 3), (1, 5), (1, 7), (1, 9), (3, 1), (3, 3), (3, 5), (3, 7), (3, 9), (5, 1), (5, 3), (5, 5), (5, 7), (5, 9), (7, 1), (7, 3), (7, 5), (7, 7), (7, 9), (9, 1), (9, 3), (9, 5), (9, 7), (9, 9)}. В данном случае пространство элементарных исходов состоит из 25 элементов: n = 25. Поскольку цифры набираются случайным образом, все элементарные исходы равновозможны и для вычисления вероятности интересующего нас события можно воспользоваться классическим методом определения вероятностей. Событие B = {номер набран правильно с первой попытки}. Число исходов, благоприятных событию В, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
Ответ: а) вероятность того, что номер набран правильно с первой попытки, равна 0,05; б) вероятность того, что номер набран правильно с первой попытки, равна 0,04.
Задача 2 Два клиента зашли в магазин. Вероятность того, что первый клиент пожелает сделать покупку, равна 0,7, для второго клиента эта вероятность равна 0,5. Найти вероятность того, что захотят сделать покупку: а) оба клиента; б) только один клиент; в) хотя бы один клиент. Решение. Обозначим события: Ai = { i -й клиент пожелает сделать покупку}, i = 1, 2; B = {оба клиента пожелают сделать покупку}; C = {только один клиент из двух пожелает сделать покупку}; D = {хотя бы один клиент из двух пожелает сделать покупку}. Согласно условию, вероятность события A 1 P (A 1) = 0,7, вероятность события A 2 P (A 2) = 0,5. Тогда вероятности противоположных событий: Определим все элементарные события данного случайного эксперимента и соответствующие вероятности:
Событие B можно представить в виде Полагая, что события Ai (i = 1, 2) – независимы, и применяя теорему умножения вероятностей независимых событий, получим
Событие С можно представить в виде Применяя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, получим
Событие D можно представить в виде где Применяя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, получим
или
Ответ: а) вероятность того, что захотят сделать покупку оба клиента, равна 0,35; вероятность того, что покупку пожелает сделать только один клиент из двух, равна 0,50; вероятность того, что покупку пожелает сделать хотя бы один клиент, равна 0,85. Задача 3. Задан закон распределения дискретной случайной величины
Решение. Составим таблицу для данной случайной величины X:
Столбцовая диаграмма, соответствующая этому ряду распределения, приведена на рисунке 29.
Рисунок 29 – Столбцовая диаграмма
Вычислим числовые характеристики данной случайной величины. Математическое ожидание
то есть среднее число вопросов, на которые студент сможет дать ответ, равно 2,25. Как следует из ряда распределения, данная случайная величина имеет две моды: Дисперсия
Среднее квадратическое отклонение Задача 4. Время пользования Интернетом в вечернее время распределено по показательному закону с математическим ожиданием, равным 0,9 часа. Найти вероятность того, что пользователь будет находиться в Интернете менее 1 часа. Найти среднее квадратическое отклонение времени пользования Интернетом. Решение. Согласно условию математическое ожидание случайной величины X, обозначающей время пользования Интернетом, равно 0,9 часа. Учитывая, что для случайной величины, распределенной по показательному закону, M [ X ] = 1/l, определяем значение параметра l = 1/ M [ X ] = 1/0,9 = 1,111. Функция плотности распределения данной случайной величины X
Определим вероятность того, что пользователь будет находиться в Интернете менее 1 часа:
Для случайной величины X, распределенной по показательному закону,
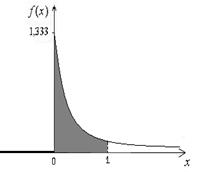
На рисунке 30 штриховкой выделена фигура, площадь которой равна вероятности
Рисунок 30 – График плотности распределения вероятностей
Контрольная работа для ЗФ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.24.49 (0.011 с.) |

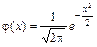 .
.
 .
.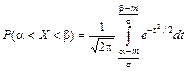 .
. не выражается через элементарные функции, но его можно выразить через специальную функцию
не выражается через элементарные функции, но его можно выразить через специальную функцию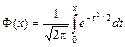 , (26)
, (26) . (27)
. (27)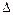 имеет вид:
имеет вид: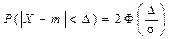 . (28)
. (28)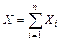 ,
,


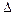 =
=  – величина отклонения случайной величины Х от ее математического ожидания.
– величина отклонения случайной величины Х от ее математического ожидания.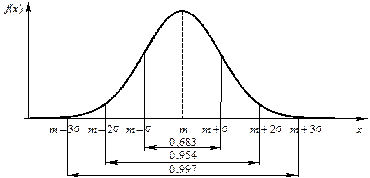
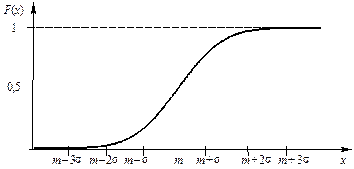
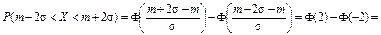
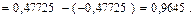
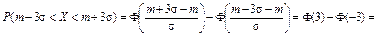
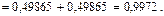
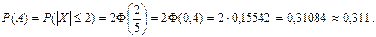


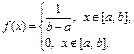
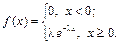
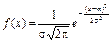 ,
, 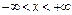



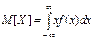 Дисперсия непрерывной случайной величины
Дисперсия непрерывной случайной величины 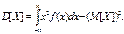 Среднее квадратическое отклонение
Среднее квадратическое отклонение 

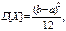
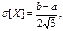
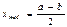 ,
, 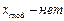
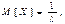
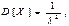

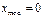 ,
,  .
.

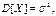
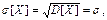
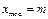 ,
, 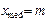 .
.
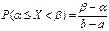


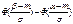
 . Вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение, моду.
. Вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение, моду.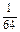
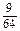
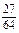
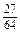
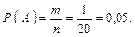

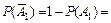
 ,
,  .
.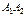
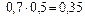
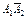
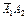
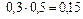
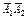
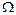
 .
.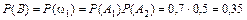 .
.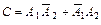 .
.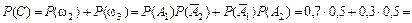
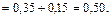
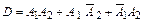 или в виде
или в виде 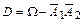 =
= 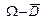 ,
, – событие, противоположное событию
– событие, противоположное событию  :
: 
 ,
,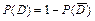 , где
, где 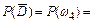
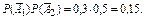
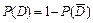 = 1 – 0,15 = 0,85.
= 1 – 0,15 = 0,85.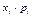

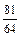
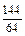
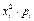
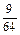
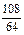
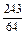

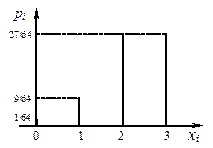
 [вопросов],
[вопросов],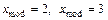 , то есть наиболее вероятное число вопросов, на которые студент сможет дать ответ, равно 2 и 3.
, то есть наиболее вероятное число вопросов, на которые студент сможет дать ответ, равно 2 и 3.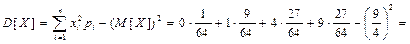
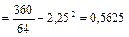 [вопросов2].
[вопросов2].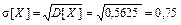 [вопросов], то есть среднее квадратическое отклонение числа вопросов, на которые студент сможет дать ответ, равно 0,75.
[вопросов], то есть среднее квадратическое отклонение числа вопросов, на которые студент сможет дать ответ, равно 0,75.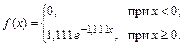
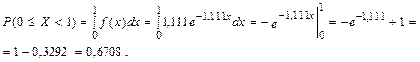
 ;
;