
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экспоненциальное распределение.Содержание книги
Поиск на нашем сайте Экспоненциальное распределение Как было отмечено в подразд. 14.4.1 экспоненциальное распределение вероятности безотказной работы является частным случаем распределения Вейбулла, когда параметр формы d=1. Это распределение однопараметрическое, то есть для записи расчетного выражения достаточно одного параметра l=const. Для этого закона верно и обратное утверждение: если интенсивность отказов постоянна, то вероятность безотказной работы как функция времени подчиняется экспоненциальному закону:
Среднее время безотказной работы при экспоненциальном законе распределения интервала безотказной работы выражается формулой:
Заменив в выражении (3.5) величину l величиной 1/Т1, получим Отметим, что вероятность безотказной работы на интервале, превышающем среднее время Т1, при экспоненциальном распределении будет менее 0,368: Р(Т1) =e-1= 0,368 (рисунок 14.5).
Рисунок 14.5 – График экспоненциального распределения Длительность периода нормальной эксплуатации до наступления старения может оказаться существенно меньше Т1, то есть интервал времени на котором допустимо пользование экспоненциальной моделью, часто бывает меньшим среднего времени безотказной работы, вычисленного для этой модели. Это легко обосновать, воспользовавшись дисперсией времени безотказной работы. Как известно [4, 13], если для случайной величины t задана плотность вероятности f(t) и определено среднее значение (математическое ожидание) Т1, то дисперсия времени безотказной работы находится по выражению:
и для экспоненциального распределения соответственно равна:
После некоторых преобразований получим:
Таким образом, наиболее вероятные значения наработки, группирующиеся в окрестности Т1, лежат в диапазоне . Важно отметить, что если объект отработал, предположим, время t без отказа, сохранив l=соnst, то дальнейшее распределение времени безотказной работы будет таким, как в момент первого включения l=соnst. Таким образом, отключение работоспособного объекта в конце интервала и новое его включение на такой же интервал множество раз приведет к пилообразной кривой
Рисунок 14.6 – Вероятность безотказной работы Другие распределения не имеют указанного свойства. Из рассмотренного следует на первый взгляд парадоксальный вывод: поскольку за все время t устройство не стареет (не меняет своих свойств), то нецелесообразно проводить профилактику или замену устройств для предупреждения внезапных отказов, подчиняющихся экспоненциальному закону. Конечно, никакой парадоксальности этот вывод не содержит, так как предположение об экспоненциальном распределении интервала безотказной работы означает, что устройство не стареет. С другой стороны, очевидно, что чем больше время, на которое включается устройство, тем больше всевозможных случайных причин, которые могут вызвать отказ устройства. Это весьма важно для эксплуатации устройств, когда приходится выбирать интервалы, через которые следует производить профилактические работы с тем, чтобы сохранить высокую надежность работы устройства. Этот вопрос подробно рассматривается в работе [1]. Модель экспоненциального распределения часто используется для априорного анализа, так как позволяет не очень сложными расчетами получить простые соотношения для различных вариантов создаваемой системы. На стадии апостериорного анализа (опытных данных) должна проводиться проверка соответствия экспоненциальной модели результатам испытаний. В частности, если при обработке результатов испытаний окажется, что На практике часто бывает, что l¹const, однако, и в этом случае его можно применять для ограниченных отрезков времени. Это допущение оправдывается тем, что при ограниченном периоде времени переменную интенсивность отказов без большой ошибки можно заменить [12, 15] средним значением: l (t) "lcр(t) = const. Распределение Рэлея. Распределение Рэлея Плотность вероятности в законе Рэлея (см. рисунок 14.7) имеет следующий вид
где d* - параметр распределения Рэлея (равен моде этого распределения [13]). Его не нужно смешивать со среднеквадратическим отклонением:
Рисунок 14.7 – Распределение Рэлея Интенсивность отказов равна: Характерным признаком распределения Рэлея является прямая линия графика l(t), начинающаяся с начала координат. Вероятность безотказной работы объекта в этом случае определится по выражению
Средняя наработка до отказа
14.4.4. Нормальное распределение (распределение Гаусса) Нормальный закон распределения характеризуется плотностью вероятности вида
где mx, sx - соответственно математическое ожидание и среднеквадратическое отклонение случайной величины х. При анализе надежности электроустановок в виде случайной величины, кроме времени, часто выступают значения тока, электрического напряжения и других аргументов. Нормальный закон - это двухпараметрический закон, для записи которого нужно знать mx и sx. Вероятность безотказной работы определяется по формуле
а интенсивность отказов - по формуле
На рисунке 14.8 изображены кривые l(t), Р(t) и f (t) для случая st<< mt, характерного для элементов, используемых в системах автоматического управления [3].
Рисунок 14.8 – Кривые нормального закона распределения В данном пособии показаны только наиболее распространенные законы распределения случайной величины. Известен целый ряд законов, так же используемых в расчетах надежности [4, 9, 11, 13, 15, 21]: гамма-распределение, c2 - распределение, распределение Максвелла, Эрланга и др. Следует отметить, что если неравенство st<< mt не соблюдается, то следует использовать усеченное нормальное распределение [19]. Для обоснованного выбора типа практического распределения наработки до отказа необходимо большое количество отказов с объяснением физических процессов, происходящих в объектах перед отказом. В высоконадежных элементах электроустановок, во время эксплуатации или испытаний на надежность, отказывает лишь незначительная часть первоначально имеющихся объектов. Поэтому значение числовых характеристик, найденное в результате обработки опытных данных, сильно зависит от типа предполагаемого распределения наработки до отказа. Как показано в [13,15], при различных законах наработки до отказа, значения средней наработки до отказа, вычисленные по одним и тем же исходным данным, могут отличаться в сотни раз. Поэтому вопросу выбора теоретической модели распределения наработки до отказа необходимо уделять особое внимание с соответствующим доказательством приближения теоретического и экспериментального распределений. 100. Основы математического моделирования. Нормальное распределение (Распределение Гаусса). Норма́льное распределе́ние,[1][2] также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей сфункцией Гаусса:
где параметр μ — математическое ожидание (среднее значение), медиана и мода распределения, а параметр σ — среднеквадратическое отклонение (σ ² — дисперсия) распределения. Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1. Важное значение нормального распределения во многих областях науки (например, в математической статистике и статистической физике) вытекает из центральной предельной теоремы теории вероятностей. Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования. При анализе надежности электроустановок в виде случайной величины, кроме времени, часто выступают значения тока, электрического напряжения и других аргументов. Нормальный закон - это двухпараметрический закон, для записи которого нужно знать mx и sx. Вероятность безотказной работы определяется по формуле
а интенсивность отказов - по формуле
где mx, sx - соответственно математическое ожидание и среднеквадратическое отклонение случайной величины х. На рис. 3.5 изображены кривые l(t), Р(t) и¦ (t) для случая st<< mt, характерного для элементов, используемых в системах автоматического управления [3].
Следует отметить, что если неравенство st<< mt не соблюдается, то следует использовать усеченное нормальное распределение [19]. 101.Методы расчета надежности электрооборудования. Методы определения надежности. Существует два основных метода определения надежности: экспериментальный и коэффициентный. Экспериментальный метод применяется при определении надежности нового оборудования, а коэффициентный метод применяется при определении надежности уже работающего оборудования. Экспериментальный метод. Дает наиболее полное представление о надежности оборудования, о причинах отказов, о слабых звеньях и способах повышения надежности. Однако для получения достоверных экспериментальных данных часто необходимо затрачивать много времени и привлекать другие значительные ресурсы. Самый доступный источник экспериментальных данных - это систематические или специально спланированные наблюдения при нормальной эксплуатации оборудования. Для реализации такого метода необходима дополнительная подготовка персонала, благодаря которой исключаются неправильное заполнение донесений об отказе оборудования, неполные сведения об условиях эксплуатации или ошибки в обработке данных. Планирование эксплуатационных испытаний или наблюдений необходимо выполнять в следующей последовательности:
=0,80; 0,90; 0,95). b=0,05) и выбирают доверительную вероятность (обычно принимают dДля расчета объема выборки задаются относительной ошибкой (обычно принимают Коэффициентный метод. ^ Коэффициент надежности l представляет собой отношение интенсивности отказов изучаемого элемента jl к интенсивности отказов некоторого базового элемента б:
С учетом изложенных положений можно перейти от обобщенной модели к расчетной формуле
где ri - коэффициент чувствительности интенсивности отказов к изменению фактора (показывает во сколько раз изменяется интенсивность при изменении значения фактора на 1%). Таким образом, для расчета интенсивности отказов коэффициентным методом необходимо определить коэффициент надежности и коэффициенты влияния (таблица 16.2), а затем по формуле (6.14) вычислить искомую эксплуатационную надежность. Если известна конструкционная надежность, то отличие расчета состоит лишь в том, что принимают
|
|||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1063; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

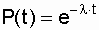 . (3.5)
. (3.5) . (3.6)
. (3.6) . (3.7) Таким образом, зная среднее время безотказной работы Т1 (или постоянную интенсивность отказов l), можно в случае экспоненциального распределения найти вероятность безотказной работы для интервала времени от момента включения объекта до любого заданного момента t.
. (3.7) Таким образом, зная среднее время безотказной работы Т1 (или постоянную интенсивность отказов l), можно в случае экспоненциального распределения найти вероятность безотказной работы для интервала времени от момента включения объекта до любого заданного момента t.
 (3.8)
(3.8) . (3.9)
. (3.9) . (3.10)
. (3.10) , то есть в диапазоне от t=0 до t=2Т1. Как видим, объект может отработать и малый отрезок времени и время t=2Т1, сохранив l=const. Но вероятность безотказной работы на интервале 2Т1 крайне низка:
, то есть в диапазоне от t=0 до t=2Т1. Как видим, объект может отработать и малый отрезок времени и время t=2Т1, сохранив l=const. Но вероятность безотказной работы на интервале 2Т1 крайне низка:
 (см. рисунок 14.6).
(см. рисунок 14.6).
 , то это является доказательством экспоненциальности анализируемой зависимости.
, то это является доказательством экспоненциальности анализируемой зависимости. , (3.11)
, (3.11) .
.
 .
. . (3.12)
. (3.12) . (3.13)
. (3.13) , (3.14)
, (3.14) , (3.15)
, (3.15)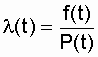 .
.

 , (3.15)
, (3.15) .
.
 . (6.13) Коэффициенты влияния Квi показывают, как изменяется интенсивность отказов изучаемого элемента при изменении дестабилизирующих или компенсирующих факторов. Они являются безразмерными. При номинальных условиях эксплуатации Квi=1,0, т.е. эксплуатационная и конструктивная интенсивность отказов равны. Для других условий 0< Квi <1.
. (6.13) Коэффициенты влияния Квi показывают, как изменяется интенсивность отказов изучаемого элемента при изменении дестабилизирующих или компенсирующих факторов. Они являются безразмерными. При номинальных условиях эксплуатации Квi=1,0, т.е. эксплуатационная и конструктивная интенсивность отказов равны. Для других условий 0< Квi <1. , (6.14)
, (6.14) , (6.15)
, (6.15) - фактическое значение учитываемого фактора в долях от номинального;
- фактическое значение учитываемого фактора в долях от номинального; .
.


