
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема подключения трёхфазного асинхронного двигателя к сети переменного тока. Звезда. Треугольник.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Схема подключения трёхфазного асинхронного двигателя к сети переменного тока. Звезда. Треугольник. Звезда и треугольник Трехфазная обмотка статора электродвигателя соединяется по схеме "звезда" или "треугольник" в зависимости от напряжения питания сети. Концы трехфазной обмотки могут быть: соединены внутри электродвигателя (из двигателя выходит три провода), выведены наружу (выходит шесть проводов), выведены в распределительную коробку (в коробку выходит шесть проводов, из коробки три). Фазное напряжение - разница потенциалов между началом и концом одной фазы. Другое определение: фазное напряжение это разница потенциалов между линейным проводом и нейтралью. Линейное напряжение - разность потенциалов между двумя линейными проводами (между фазами).
Внимание: Несмотря на то, что мощность для соединений в звезду и треугольник вычисляется по одной формуле, подключение одного и того же электродвигателя разным способом в одну и туже электрическую сеть приведет к потреблению разной мощности. При этом не правильное подключение электродвигателя, может привести к расплавлению обмоток статора. Пример: Допустим электродвигатель был подключен по схеме "звезда" к трехфазной сети переменного тока Uл=380 В (соответственно Uф=220 В) и потреблял ток Iл=1 А. Полная потребляемая мощность: S = 1,73∙380∙1 = 658 Вт. Теперь изменим схему соединения на "треугольник", линейное напряжение останется таким же Uл=380 В, а фазовое напряжение увеличится в корень из 3 раз Uф=Uл=380 В. Увеличение фазового напряжения приведет к увеличению фазового тока в корень из 3 раз. Таким образом линейный ток схемы "треугольник" будет в три раза больше линейного тока схемы "звезда". А следовательно и потребляемая мощность будет в 3 раза больше: S = 1,73∙380∙3 = 1975 Вт. Таким образом, если двигатель рассчитан на подключение к трехфазной сети переменного тока по схеме "звезда", подключение данного электродвигателя по схеме "треугольник" может привести к его поломке. Если в нормальном режиме электродвигатель подключен по схеме "треугольник", то для уменьшения пусковых токов на время пуска его можно соединить по схеме звезда. При этом вместе с пусковым током уменьшится также пусковой момент.
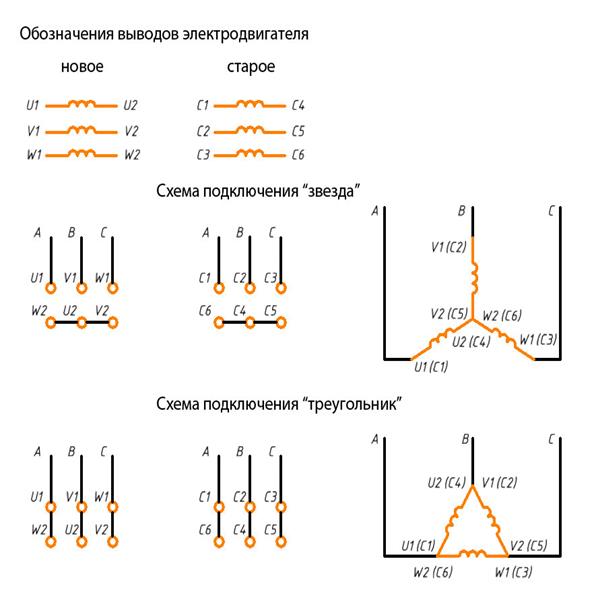
Подключение электродвигателя по схеме звезда и треугольник
Обозначение выводов статора трехфазного электродвигателя Обозначение выводов обмоток статора вновь разрабатываемых трехфазных машин согласно ГОСТ 26772-85 [2]
Обозначение выводов обмоток статора ранее разработанных и модернизируемых трехфазных машин согласно ГОСТ 26772-85
Схема управления электрическим двигателем с помощью магнитных пускателей. Реверсивная схема
Реверсивная схема подключения трехфазного асинхронного электродвигателя к трехфазной сети переменного электрического тока через магнитные пускатели
Расчёт резисторов
В этой статье рассмотрим как можно с помощью параллельного и последовательного включения резисторов и конденсаторов подобрать нужный номинал радиодетали, при отсутствии нужного. Расчёт производится по формулам расчёта сопротивления и ёмкости для параллельного и последовательного включения, а также с помощью удобной таблицы подбора ёмкости и сопротивления.
Резисторы Широко применяются в радиоприёмниках, усилителях сигналов и во многих других схемах. Они служат для ограничения тока, создания падения напряжения, регулирования частоты, громкости и других сигналов. Обозначаются на схемах буквой R. Сопротивление резистора измеряется в Омах. Для больших сопротивлений используют единицы: килоомы (1кОм=1000Ом), мегаомы (1Мом=1000кОм). Кроме сопротивления резисторы характеризуются мощностью рассеяния, это такая наибольшая мощность, которую резистор может выдержать длительное время. Мощность рассеяния измеряется в ваттах (Вт). Ещё один показатель — это наибольшее возможное отклонение действительного сопротивления от номинального, указанного на резисторе, выражается в %. Резисторы бывают постоянные (не изменяют своего сопротивления) и переменные(изменяют сопротивление в зависимости от положения движка резистора). Иногда, при сборке схемы не оказывается под рукой резистора нужного номинала. В этом случае в большинстве случаев можно заменить резистор на ближайший по номиналу — например вместо 110 Ом можно использовать резистор номиналом 100 или 120 Ом. А если нет и ближайшего по номиналу или требуется точное значение сопротивления, то можно составить нужное сопротивление с помощью последовательного или параллельного соединения нескольких резисторов. Последовательное соединение резисторов:
последовательное соединение резисторов
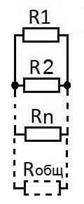
При последовательном соединении резисторов их общее сопротивление равно их сумме: Rобщ = R1+R2+…+Rn. Параллельное соединение резисторов:
Параллельное соединение резисторов
При параллельном соединении резисторов их общее сопротивление рассчитывается по формуле: 1/Rобщ = 1/R1 + 1/R2 +…+1/Rn или Rобщ = 1/(1/R1 + 1/R2 +…+1/Rn). На практике для подбора нужного сопротивления обычно включают параллельно два резистора, в этом случае формула примет вид: Rобщ = R1*R2/(R1+R2). Ещё можно отметить, что при включении резисторов одинакового сопротивления, то их общее сопротивление будет равно половине сопротивления каждого их них. Мощность рассеяния, в этом случае, увеличится в 2 раза. Также при параллельном соединении общее сопротивление всегда меньше наименьшего из включенных в параллель резисторов. Конденсаторы Конденсаторы, как и резисторы, тоже очень широко применяются. Конденсатор это накопитель энергии, в простейшем виде это две пластины, между которыми находится диэлектрик, в качестве диэлектрика может быть просто воздух. Конденсаторы также бывают постоянной и переменной ёмкости. Единицей ёмкости является фарада(Ф). На практике используют меньшие ёмкости, их выражают в микрофарадах(1Ф=1 000 000 мкФ), нанофарадах(1мкФ = 1 000 нФ), пикофарадах(1нФ=1 000 пФ). Также конденсаторы характеризуются рабочим напряжением, выражаемом в вольтах (В). Превышение на конденсаторе напряжения выше рабочего может привести к «пробою» диэлектрика конденсатора. Конденсатор не проводит постоянный ток, а переменному току оказывает сопротивление, которое вычисляется по формуле: Хс = 1/(2 π fC), где
Рассмотрим как можно собрать нужную ёмкость из имеющихся под рукой. Последовательное включение конденсаторов:
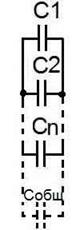
Последовательное соединение конденсаторов При последовательном соединении конденсаторов их общая ёмкость рассчитывается по формуле, очень похожей на формулу для параллельного включения резисторов: Собщ = 1/(1/С1+1/С2+…+1/Сn). Но чаще тоже используют два конденсатора, тогда формула упрощается: Собщ = С1*С2/(С1+С2). Также, при включении конденсаторов с одинаковой ёмкостью их общая ёмкость будет в два раза меньше ёмкости каждого из них. Рабочее напряжение такого сборного конденсатора увеличится в 2 раза. Параллельное включение конденсаторов:
Расчёт пусковых резисторов Пусковая диаграмма Под пусковой диаграммой понимают совокупность двух или более искусственных механических характеристик, которые используются при пуске асинхронного двигателя в пределах от М1 до М2 , где М2 – момент переключения, М2 = (1,1 – 1,25) МСТ; М1 – предельный момент не должен превышать момента критического МК(максимального) М1 = (0,8 – 0,9) МКР. По принятым значениям М1 и М2 определяют какое будет число ступеней m пусковой диаграммы: где Если m – получилось не целым числом, то нужно изменить М1 и М2 и повторить расчет. При незначительном расхождении полученного m от целого числа можно пересчитать только момент переключения или при новом Пусковая диаграмма на три ступени, m= 3 приведена на рис. 5.1 для схемы включения пусковых сопротивлений в цепь ротора, показанной на рис. 5.2.
Рис. 5.1. Пусковая диаграмма m= 3
Рис. 5.2. Схема сопротивлений в цепи ротора при m= 3 Рабочие участки искусственных характеристик в пределах пусковой диаграммы от М1 до М2 принимают линейными. Согласно рис. 5.1 из точки «в» ( Основные понятия теории эксплуатации.
Распределение Вейбулла. Распределение Вейбулла Опыт эксплуатации очень многих электронных приборов и значительного количества электромеханической аппаратуры показывает, что для них характерны три вида зависимостей интенсивности отказов от времени (рисунок 14.4), соответствующих трем периодам жизни этих устройств [3, 8, 10, 19].
Нетрудно увидеть, что этот рисунок аналогичен рисунку 14.3, так как график функции l(t) соответствует закону Вейбулла. Указанные три вида зависимостей интенсивности отказов от времени можно получить, используя для вероятностного описания случайной наработки до отказа двухпараметрическое распределение Вейбулла [12, 13, 15]. Согласно этому распределению плотность вероятности момента отказа
где d - параметр формы (определяется подбором в результате обработки экспериментальных данных, d > 0); l- параметр масштаба,
Интенсивность отказов определяется по выражению
Вероятность безотказной работы
а средняя наработки до отказа
Отметим, что при параметре d=1 распределение Вейбулла переходит в экспоненциальное, а при d=2 - в распределение Рэлея. При d<1 интенсивность отказов монотонно убывает (период приработки), а при d>1 монотонно возрастает (период износа), см. рисунок 14.4. Следовательно, путем подбора параметра d можно получить, на каждом из трех участков, такую теоретическую кривую l(t), которая достаточно близко совпадает с экспериментальной кривой, и тогда расчет требуемых показателей надежности можно производить на основе известной закономерности. Распределение Вейбулла достаточно близко подходит для ряда механических объектов (к примеру, шарикоподшипников), оно может быть использовано при ускоренных испытаниях объектов в форсированном режиме [12]. Распределение Рэлея. Распределение Рэлея Плотность вероятности в законе Рэлея (см. рисунок 14.7) имеет следующий вид
где d* - параметр распределения Рэлея (равен моде этого распределения [13]). Его не нужно смешивать со среднеквадратическим отклонением:
Рисунок 14.7 – Распределение Рэлея Интенсивность отказов равна: Характерным признаком распределения Рэлея является прямая линия графика l(t), начинающаяся с начала координат. Вероятность безотказной работы объекта в этом случае определится по выражению
Средняя наработка до отказа
14.4.4. Нормальное распределение (распределение Гаусса) Нормальный закон распределения характеризуется плотностью вероятности вида
где mx, sx - соответственно математическое ожидание и среднеквадратическое отклонение случайной величины х. При анализе надежности электроустановок в виде случайной величины, кроме времени, часто выступают значения тока, электрического напряжения и других аргументов. Нормальный закон - это двухпараметрический закон, для записи которого нужно знать mx и sx. Вероятность безотказной работы определяется по формуле
а интенсивность отказов - по формуле
На рисунке 14.8 изображены кривые l(t), Р(t) и f (t) для случая st<< mt, характерного для элементов, используемых в системах автоматического управления [3].
Рисунок 14.8 – Кривые нормального закона распределения В данном пособии показаны только наиболее распространенные законы распределения случайной величины. Известен целый ряд законов, так же используемых в расчетах надежности [4, 9, 11, 13, 15, 21]: гамма-распределение, c2 - распределение, распределение Максвелла, Эрланга и др. Следует отметить, что если неравенство st<< mt не соблюдается, то следует использовать усеченное нормальное распределение [19]. Для обоснованного выбора типа практического распределения наработки до отказа необходимо большое количество отказов с объяснением физических процессов, происходящих в объектах перед отказом. В высоконадежных элементах электроустановок, во время эксплуатации или испытаний на надежность, отказывает лишь незначительная часть первоначально имеющихся объектов. Поэтому значение числовых характеристик, найденное в результате обработки опытных данных, сильно зависит от типа предполагаемого распределения наработки до отказа. Как показано в [13,15], при различных законах наработки до отказа, значения средней наработки до отказа, вычисленные по одним и тем же исходным данным, могут отличаться в сотни раз. Поэтому вопросу выбора теоретической модели распределения наработки до отказа необходимо уделять особое внимание с соответствующим доказательством приближения теоретического и экспериментального распределений. 100. Основы математического моделирования. Нормальное распределение (Распределение Гаусса). Норма́льное распределе́ние,[1][2] также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей сфункцией Гаусса:
где параметр μ — математическое ожидание (среднее значение), медиана и мода распределения, а параметр σ — среднеквадратическое отклонение (σ ² — дисперсия) распределения. Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1. Важное значение нормального распределения во многих областях науки (например, в математической статистике и статистической физике) вытекает из центральной предельной теоремы теории вероятностей. Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования. При анализе надежности электроустановок в виде случайной величины, кроме времени, часто выступают значения тока, электрического напряжения и других аргументов. Нормальный закон - это двухпараметрический закон, для записи которого нужно знать mx и sx. Вероятность безотказной работы определяется по формуле
а интенсивность отказов - по формуле
где mx, sx - соответственно математическое ожидание и среднеквадратическое отклонение случайной величины х. На рис. 3.5 изображены кривые l(t), Р(t) и¦ (t) для случая st<< mt, характерного для элементов, используемых в системах автоматического управления [3].
Следует отметить, что если неравенство st<< mt не соблюдается, то следует использовать усеченное нормальное распределение [19]. 101.Методы расчета надежности электрооборудования. Методы определения надежности. Существует два основных метода определения надежности: экспериментальный и коэффициентный. Экспериментальный метод применяется при определении надежности нового оборудования, а коэффициентный метод применяется при определении надежности уже работающего оборудования. Экспериментальный метод. Дает наиболее полное представление о надежности оборудования, о причинах отказов, о слабых звеньях и способах повышения надежности. Однако для получения достоверных экспериментальных данных часто необходимо затрачивать много времени и привлекать другие значительные ресурсы. Самый доступный источник экспериментальных данных - это систематические или специально спланированные наблюдения при нормальной эксплуатации оборудования. Для реализации такого метода необходима дополнительная подготовка персонала, благодаря которой исключаются неправильное заполнение донесений об отказе оборудования, неполные сведения об условиях эксплуатации или ошибки в обработке данных. Планирование эксплуатационных испытаний или наблюдений необходимо выполнять в следующей последовательности:
=0,80; 0,90; 0,95). b=0,05) и выбирают доверительную вероятность (обычно принимают dДля расчета объема выборки задаются относительной ошибкой (обычно принимают Коэффициентный метод. ^ Коэффициент надежности l представляет собой отношение интенсивности отказов изучаемого элемента jl к интенсивности отказов некоторого базового элемента б:
С учетом изложенных положений можно перейти от обобщенной модели к расчетной формуле
где ri - коэффициент чувствительности интенсивности отказов к изменению фактора (показывает во сколько раз изменяется интенсивность при изменении значения фактора на 1%). Таким образом, для расчета интенсивности отказов коэффициентным методом необходимо определить коэффициент надежности и коэффициенты влияния (таблица 16.2), а затем по формуле (6.14) вычислить искомую эксплуатационную надежность. Если известна конструкционная надежность, то отличие расчета состоит лишь в том, что принимают Схема подключения трёхфазного асинхронного двигателя к сети переменного тока. Звезда. Треугольник. Звезда и треугольник Трехфазная обмотка статора электродвигателя соединяется по схеме "звезда" или "треугольник" в зависимости от напряжения питания сети. Концы трехфазной обмотки могут быть: соединены внутри электродвигателя (из двигателя выходит три провода), выведены наружу (выходит шесть проводов), выведены в распределительную коробку (в коробку выходит шесть проводов, из коробки три). Фазное напряжение - разница потенциалов между началом и концом одной фазы. Другое определение: фазное напряжение это разница потенциалов между линейным проводом и нейтралью. Линейное напряжение - разность потенциалов между двумя линейными проводами (между фазами).
Внимание: Несмотря на то, что мощность для соединений в звезду и треугольник вычисляется по одной формуле, подключение одного и того же электродвигателя разным способом в одну и туже электрическую сеть приведет к потреблению разной мощности. При этом не правильное подключение электродвигателя, может привести к расплавлению обмоток статора. Пример: Допустим электродвигатель был подключен по схеме "звезда" к трехфазной сети переменного тока Uл=380 В (соответственно Uф=220 В) и потреблял ток Iл=1 А. Полная потребляемая мощность: S = 1,73∙380∙1 = 658 Вт. Теперь изменим схему соединения на "треугольник", линейное напряжение останется таким же Uл=380 В, а фазовое напряжение увеличится в корень из 3 раз Uф=Uл=380 В. Увеличение фазового напряжения приведет к увеличению фазового тока в корень из 3 раз. Таким образом линейный ток схемы "треугольник" будет в три раза больше линейного тока схемы "звезда". А следовательно и потребляемая мощность будет в 3 раза больше: S = 1,73∙380∙3 = 1975 Вт. Таким образом, если двигатель рассчитан на подключение к трехфазной сети переменного тока по схеме "звезда", подключение данного электродвигателя по схеме "треугольник" может привести к его поломке. Если в нормальном режиме электродвигатель подключен по схеме "треугольник", то для уменьшения пусковых токов на время пуска его можно соединить по схеме звезда. При этом вместе с пусковым током уменьшится также пусковой момент.
Подключение электродвигателя по схеме звезда и треугольник
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.013 с.) |



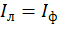


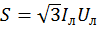


 Расчёт сопротивления резисторов и ёмкости конденсаторов
Расчёт сопротивления резисторов и ёмкости конденсаторов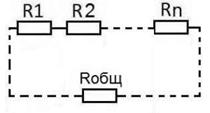

 , (5.6)
, (5.6) .
. при том же М1:
при том же М1: (5.7)
(5.7) .
.

 ) в точку (
) в точку (  , М = 0) проводят прямую линию – это первая искусственная характеристика. В точке пересечения с
, М = 0) проводят прямую линию – это первая искусственная характеристика. В точке пересечения с  проводят горизонталь до
проводят горизонталь до  (линия cd). Из точки «d» в точку (
(линия cd). Из точки «d» в точку ( 


 , (3.1)
, (3.1) .
. (3.2)
(3.2) , (3.3)
, (3.3)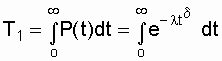 . (3.4)
. (3.4) , (3.11)
, (3.11) .
.
 .
. . (3.12)
. (3.12) . (3.13)
. (3.13) , (3.14)
, (3.14) , (3.15)
, (3.15)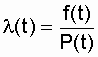 .
.

 , (3.15)
, (3.15) .
.
 . (6.13) Коэффициенты влияния Квi показывают, как изменяется интенсивность отказов изучаемого элемента при изменении дестабилизирующих или компенсирующих факторов. Они являются безразмерными. При номинальных условиях эксплуатации Квi=1,0, т.е. эксплуатационная и конструктивная интенсивность отказов равны. Для других условий 0< Квi <1.
. (6.13) Коэффициенты влияния Квi показывают, как изменяется интенсивность отказов изучаемого элемента при изменении дестабилизирующих или компенсирующих факторов. Они являются безразмерными. При номинальных условиях эксплуатации Квi=1,0, т.е. эксплуатационная и конструктивная интенсивность отказов равны. Для других условий 0< Квi <1. , (6.14)
, (6.14) , (6.15)
, (6.15) - фактическое значение учитываемого фактора в долях от номинального;
- фактическое значение учитываемого фактора в долях от номинального; .
.


