
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равномерный закон распределенияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Непрерывная случайная величина, которая принимает значения, только принадлежащие отрезку [ a, b ] с постоянной плотностью распределения, называется распределенной по равномерному закону. Функция плотности распределения вероятностей определяется соотношением
Найдем функцию распределения данной случайной величины:
Графики функций f (x) и F (x) изображены на рисунках 15 и 16.
Математическое ожидание случайной величины X, распределенной по равномерному закону на участке [ a, b ], как следует из механической интерпретации (центр массы), равно абсциссе середины участка: M [ X ] = (a + b)/2. Этот же результат можно получить и вычисляя интеграл:
Дисперсию случайной величины X также можно найти, исходя из механической интерпретации (момент инерции распределения относительно центра массы): D [ X ] = (b – a)2/12. Тот же результат можно получить, вычисляя интеграл:
Среднее квадратическое отклонение равномерно распределенной случайной величины
Моды равномерное распределение не имеет; его медиана из соображений симметрии равна (a + b)/2. Из тех же соображений симметрии коэффициент асимметрии A [ X ] = 0. Коэффициент эксцесса случайной величины X равен –1,2: Ex [ X ] = –1,2; как и следовало ожидать, он отрицателен. Примером случайной величины, которая имеет равномерный закон распределения, является время ожидания регулярных событий, например, время ожидания поезда в метрополитене, время ожидания автобуса определенного маршрута на остановке. Рассмотрим несколько примеров случайных величин, имеющих равномерное распределение. При проведении измерений некоторой величины с помощью прибора с крупными делениями ошибки округления распределены по равномерному закону. Очевидно, что равномерное распределение имеют и ошибки, возникающие от округления данных при расчетах.
Пример 17 Поезда метрополитена идут с интервалом в 4 минуты. Пассажир приходит на платформу поезда в произвольный момент времени. Найти вероятность того, что он будет ожидать прихода поезда не более одной минуты. Найти среднее время ожидания поезда пассажиром, вычислить дисперсию и среднее квадратическое отклонение времени ожидания поезда пассажиром.
Решение. Рассмотрим случайную величину X – время ожидания пассажиром поезда. Все возможные значения данной случайной величины принадлежат отрезку [0; 4], и, согласно условию, все эти значения равновозможны. Следовательно, случайная величина распределена по равномерному закону с параметрами a = 0 и b = 4. Функция плотности распределения вероятностей данной случайной величины:
Найдем вероятность того, что пассажир будет ожидать поезд не более одной минуты:
На рисунке 17 штриховкой выделена фигура, площадь которой равна вероятности
Рисунок 17 – График плотности распределения вероятностей
Среднее время ожидания прихода поезда пассажиром
M [ X ] = (a + b)/2 = (0 + 4)/2 = 2,0 [мин].
Дисперсия
Среднее квадратическое отклонение
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 629; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.57.57 (0.009 с.) |






 .
.
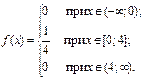
 .
.






