
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределения непрерывных случайных величин.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Равномерное распределение непрерывной случайной величины
Определение. Говорят, что непрерывная случайная величина имеет равномерное распределение на отрезке
Постоянная величина С определяется из условия равенства единице площади, ограниченной кривой распределения.
0 a b x Получаем
1 0 a b x
Для того чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы ее значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны. Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения:
Вероятность попадания случайной величины в заданный интервал:
Показательное распределение непрерывной случайной величины
Определение. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины Х, плотность вероятности которой определяется формулой
где l - положительное число. Найдем закон распределения.
Графики функции распределения и плотности распределения:
l 1 0 x 0 x
Найдем математическое ожидание случайной величины, подчиненной показательному распределению:
Результат получен с использованием того факта, что
Для нахождения дисперсии найдем величину
Дважды интегрируя по частям, аналогично рассмотренному случаю, получим:
Тогда Таким образом: Очевидно, что в случае показательного распределения математическое ожидание и среднее квадратическое отклонение равны. Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал:
Показательное распределение широко используется в теории надежности. Допустим, некоторое устройство начинает работать в момент времени Обозначим Т непрерывную случайную величину – длительность безотказной работы устройства. Таким образом, функция распределения Вероятность противоположного события (безотказная работа в течение времени t) равна Определение. Функцией надежности Часто на практике длительность безотказной работы подчиняется показательному закону распределению. Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать. Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения. Функция надежности для какого- либо устройства при показательном законе распределения равна:
Данное соотношение называют показательным законом надежности. Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t. Таким образом, безотказная работа устройства зависит только от интенсивности отказов l и не зависит от безотказной работы устройства в прошлом. Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 500; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.01 с.) |

 , если на этом отрезке плотность распределения случайной величины постоянна, а вне него равна нулю:
, если на этом отрезке плотность распределения случайной величины постоянна, а вне него равна нулю:



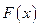 на отрезке
на отрезке 














 :
: .
.


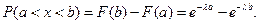
 , а через какое– то время t происходит отказ устройства.
, а через какое– то время t происходит отказ устройства. определяет вероятность отказа за время длительностью t.
определяет вероятность отказа за время длительностью t.
 называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.
называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.



