
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальный закон распределения непрерывной случайной величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, плотность вероятности которой определяется по формуле:
где Нормальный закон распределения называется также законом Гаусса. Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения. Найдем функцию распределения
График плотности нормального распределения называется нормальной кривой или кривой Гаусса. Нормальная кривая обладает следующими свойствами: 1) Функция определена на всей числовой оси. 2) При всех х функция распределения принимает только положительные значения. 3) Ось 4) Найдем экстремум функции:
Т.к. при 5) Функция является симметричной относительно прямой
6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.
При В этих точках значение функции равно Построим графики при
Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается. Если При
Функция Лапласа
Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал:
Обозначим: Тогда: Интеграл
которая называется функцией Лапласа или интегралом вероятностей. Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах. График функции Лапласа имеет вид
Функция Лапласа обладает следующими свойствами: 1) Функцию Лапласа также называют функцией ошибок. Нормированная функция Лапласа связана с функцией Лапласа соотношением:
График нормированной функции Лапласа имеет вид:
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм. Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
Если принять D
т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю. Это правило называется правилом трех сигм. Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение. Пример. Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожиданием Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100×65 = 6500) не превосходит 6600 – 6500 = 100 т. Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально. Получаем:
Пример. Нормально распределенная случайная величина Х задана своими параметрами – Плотность распределения определяется по формуле:
Найдем вероятность попадания случайной величины в интервал
Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2:
Тот же результат может быть получен с использованием нормированной функции Лапласа:
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |

 .
. - математическое ожидание, а
- математическое ожидание, а  - среднее квадратическое отклонение случайной величины
- среднее квадратическое отклонение случайной величины  .
.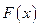 :
: .
.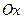 является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.
является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.
 при
при  и
и  при
при  , то в точке
, то в точке  функция имеет максимум, равный
функция имеет максимум, равный  .
. входит в функцию плотности распределения в квадрате.
входит в функцию плотности распределения в квадрате.
 и
и  вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.
вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб. и трех возможных значениях среднего квадратичного отклонения
и трех возможных значениях среднего квадратичного отклонения 
 и
и  :
:
 , то график смещается в сторону положительного направления оси
, то график смещается в сторону положительного направления оси  – в сторону отрицательного направления оси
– в сторону отрицательного направления оси 
 кривая называется нормированной. Уравнение нормированной кривой имеет вид
кривая называется нормированной. Уравнение нормированной кривой имеет вид
 .
.
 .
. не выражается через элементарные функции. Введём в рассмотрение функцию:
не выражается через элементарные функции. Введём в рассмотрение функцию: ,
,
 2)
2)  3)
3) 



 .
. , то получаем с использованием таблиц значений функции Лапласа:
, то получаем с использованием таблиц значений функции Лапласа:
 т. и средним квадратичным отклонением
т. и средним квадратичным отклонением  т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.
т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется. .
. – математическое ожидание и
– математическое ожидание и 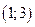 , найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.
, найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.







