
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции нормального распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим, как определяется вероятность с помощью табл.2.6. Пусть имеется интервал от а = 2,72 до b = 2,96; известны также характеристики Задача нахождения вероятностей упрощается, если а и b симметричны относительно Интегралы вероятности (2.25) и (2.26), играющие большую роль, можно вычислять и без применения таблиц путем численного интегрирования на компьютере или с помощью пакета «Stat». Часто приходится решать обратную задачу – находить интервал возможных значений случайной величины t при заданных вероятностях p, a, q или b. Если задана вероятность p = F (t), то соответствующее ей значение t называется квантилью распределения. Она является функцией, обратной интегралу вероятности (2.20), и обозначается t = F –1(p). Квантиль можно найти интерполяцией данных табл.2.6. Например, задана вероятность p = 0,9. В таблице имеются значения p = 0,8849 (при t = 1,2) и p = 0,9032 (при t = 1,3). Интерполируя эти значения, найдем, что при p = 0,9 квантиль t = 1,28. Квантили, соответствующие вероятностям 1/4; 2/4; 3/4, называются квартилями. Вторая квартиль, соответствующая вероятности p = 0,5, называется медианой распределения. Наиболее часто используют значения t, соответствующие заданной вероятности q = Ф(t), они называются коэффициентами вероятности и служат критериями принятия разнообразных решений. Для нахождения коэффициента вероятности можно воспользоваться интерполяцией данных табл.2.6, но лучше иметь специальную табл.2.7 зависимости t от Ф(t). Например, задана вероятность q = 0,96, тогда соответствующий ей коэффициент вероятности t = 2,054. Табл.2.7 может быть использована и для нахождения квантилей. По заданной вероятности p вычисляется вероятность q = 2 p – 1 и по табл.2.7 определяется квантиль. Например, дана вероятность p = 0,9. Вычисляем q = 2×0,9 – 1 = 0,8, соответствующая ей квантиль t = 1,282.
Таблица 2.7 Коэффициенты вероятности t при заданной вероятности q = Ф(t)
На практике наиболее часто используются значения вероятностей q = 0,5 и q = 0,9 (b = 0,5 и b = 0,01). Им соответствуют коэффициенты вероятности t = 1,960 и t = 2,576. С другой стороны, часто задаются значения t = 2 и t = 3, им соответствуют вероятности q = 0,9545 и q = 0,9973 (см. табл.2.6).
2.2.3. Логарифмически-нормальный закон распределения
В тесной связи с нормальным находится логарифмически-нормальный (сокращенно логнормальный) закон распределения, широко применяемый в геохимии. Замечено, что этим законом удовлетворительно описывается частота появления низких содержаний химических элементов. Академик А.Н.Колмогоров теоретически обосновал логнормальное распределение частиц при дроблении, что используется при гранулометрическом анализе обломочных пород. Логнормальный закон описывает ситуацию, когда нормальному распределению подчиняются логарифмы значений случайной величины. При расчетах вначале находят натуральные или десятичные логарифмы значений случайной величины. Далее вся работа ведется с логарифмами: вычисляют их среднее значение, дисперсию, среднеквадратичное отклонение, асимметрию, эксцесс, а по таблицам нормального закона определяют вероятности. Какие логарифмы – натуральные или десятичные – использовать для расчетов, не играет роли, потому что они связаны постоянным множителем: натуральные логарифмы в 2,3026 раз больше десятичных (2,3026 = ln10).
Случайная величина в логнормальном законе, в отличие от нормального, имеет область существования от нуля до +¥. Если присутствуют нулевые значения (или следы), что нередко бывает при спектральном и химическом анализах, то это вызывает трудности, так как логарифм нуля равен –¥. Обычно нулевые содержания заменяют какими-то минимальными значениями, например пределом чуствительности анализа. Существуют также способы обработки усеченных распределений, позволяющие получать статистические характеристики при отбрасывании крайних исходных значений. Обозначим логарифм случайной величины: z = ln х. Плотность вероятности логарифмов описывается формулой нормального закона (2.22)
где Плотность вероятности исходных значений х выражается формулой логнормального закона
Дисперсия исходных данных также определяется соотношением
При малой дисперсии кривые плотности вероятности логнормального и нормального законов близки между собой и в пределе, при стремлении дисперсии к нулю, совпадают.
2.2.4. Распределение Стьюдента Распределение Стьюдента, называемое также t -распределением, играет большую роль – с его помощью проверяют гипотезы о равенстве средних значений случайных величин. Функция распределения Стьюдента выражается интегралом:
соответственно, плотность вероятности имеет вид
где k – число степеней свободы, Г – гамма-функция, выражаемая интегралом: Г(х) = Число степеней свободы зависит от числа измерений n случайной величины и от существа поставленной задачи. Если проверяется гипотеза о равенстве вычисленного среднего значения какому-то заранее заданному числу, то k = n – 1. Если сравниваются два средних значения из двух совокупностей с числом измерений n 1 и n 2, то k = n 1 + n 2 – 2. Могут быть и другие варианты гипотез. Из функции (2.33) следует, что случайная величина t может принимать любые значения в пределах от –¥ до +¥. Особенность распределения Стьюдента состоит в том, что его функции зависят от числа степеней свободы, а они, в свою очередь, – от числа измерений. При увеличении значения k распределение приближается к нормальному и в пределе (при k = ¥) совпадает с ним. Практически уже при k = 20 можно пользоваться таблицами нормального распределения. Функция распределения (2.32) обычно приводится в табличном виде. Подробные сведения даны в справочнике Л.Н.Большева, Н.В.Смирнова [4]. Здесь приведены лишь некоторые значения (табл.2.8), из них видно, как с увеличением числа k функция распределения Стьюдента приближается к нормальному закону (последняя графа табл.2.8). Плотность вероятности (2.33) имеет симметричный график, похожий на кривую нормального закона, но более вытянутый по горизонтальной оси (рис.2.10). При увеличении значения k график приближается к кривой нормального закона.
Таблица 2.8 Функция распределения Стьюдента Fk (t) в зависимости от числа степеней свободы k
Значения плотности вероятности обычно находят по таблицам, но их несложно вычислить, преобразовав формулу (2.33) к следующему виду:
Для нахождения Аk достаточно знать одно значение, например А 1 =
Таблица 2.9 Плотность вероятности распределения Стьюдента fk (t) в зависимости от числа степеней свободы k
Асимметрия распределения Стьюдента равна нулю, а эксцесс отрицательный. Как и в случае нормального закона, для распределения Стьюдента может быть вычислена функция Ф k (t) = 2 Fk (t) – 1, которая характеризует вероятность q попадания случайной величины в симметричный интервал от – t до + t. На практике для принятия решений чаще используется противоположный показатель b = 1 – q. Можно составить таблицу зависимости b от t при различных степенях свободы k. Но гораздо важнее знать обратную функцию: чему равно значение коэффициента t при заданной вероятности b и известной степени свободы k (табл.2.10), так как коэффициент t часто используют в качестве критерия принятия решений. Именно такие таблицы с различными вариациями и приводятся в разнообразных справочниках. Например, задана вероятность b = 0,05 = 5 % и число степеней свободы k = 15. Из табл.2.10 имеем t = 2,131.
Таблица 2.10 Коэффициенты вероятности t распределения Стьюдента при заданной вероятности b и степени свободы k
Если число степеней свободы велико (несколько десятков и более), то можно пользоваться таблицами нормального закона (см. табл.2.7). Так, при b = 0,01 имеем q = 1 – b = 1 – 0,01 = 0,99 и по табл.2.7 находим t = 2,576. Таким образом, распределения нормальное и Стьюдента близки между собой. При малом числе измерений (и, соответственно, степеней свободы) более надежные выводы могут быть сделаны по таблицам распределения Стьюдента, а при большом числе наблюдений следует пользоваться таблицами нормального закона.
2.2.5. Распределение c2
Распределение c2 служит преимущественно для проверки гипотез о соответствии наблюдаемых частот теоретичеcким законам распределения. Плотность вероятности распределения описывается формулой
где k – число степеней свободы, зависящее от числа классов гистограммы nk (обычно k = nk – 3).
При увеличении числа степеней свободы распределение c2 приближается к нормальному с математическим ожиданием k и дисперсией 2 k. Практически при числе степеней свободы k > 30 можно переходить к таблицам нормального распределения, заменив величину c2 нормированной случайной величиной t:
Для практических целей требуется иметь таблицу коэффициентов вероятности, играющих роль критериев. В зависимости от вероятности a при заданной степени свободы k (табл.2.11) критерию c2 соответствует заштрихованная площадь на рис.2.11.
Таблица 2.11 Коэффициенты вероятности распределения c2
при заданных вероятности a и числе степеней свободы k
8 Пример 2.3. Выбрана вероятность a = 0,05, число степеней свободы k = 15. Необходимо найти c2. Из табл.2.11 получаем c2 = 25,0. Если число степеней свободы большое (например, k = 50), а вероятность та же, то воспользуемся табл.2.6 нормального закона, для чего найдем Ф(t) = 1 – 2a = 0,90, ей соответствует найденное интерполяцией значение t = 1,645. Из формулы (2.35) следует, что c2 = 66,45. Для сравнения точное значение c2 = 67,50.7
2.2.6. Распределение Фишера
Распределение Фишера,называемое также F -распределением, используется для проверки гипотезы о равенстве дисперсий случайных величин. В качестве критерия служит отношение несмещенных оценок дисперсий F =
где k 1 и k 2 – количество степеней свободы, зависящее от числа измерений случайных величин n 1 и n 2, т.е. k 1 = n 1 – 1 и k 2 = n 2 – 1. График плотности вероятности асимметричен (рис.2.12) и имеет максимум (моду)
Практическое значение имеет зависимость коэффициента t (критерия) от вероятности a (ей соответствует заштрихованная площадь на рис.2.12) при заданных степенях свободы k 1 и k 2. Оценивается вероятность того, что отношение
Таблица 2.12 Коэффициенты вероятности F -распределения при a = 0,05 = 5 %
Коэффициент t зависит от трех величин: вероятности a, степеней свободы k 1 и k 2, что трудно отобразить в одной таблице, поэтому применяется серия таблиц с различными значениями вероятности a. В качестве примера приведена табл.2.12 значений коэффициента t при наиболее часто используемой вероятности a = 0,05.
8 Пример 2.4. Необходимо сравнить две дисперсии: Находим отношение F = 5,22/1,86 = 2,81, степени свободы k 1 = 16 – 1 = 15, k 2 = 31 – 1 = 30. Из табл.2.12 имеем t = 2,01. Поскольку значение F = 2,81 больше критерия t = 2,01, дисперсии
2.2.7. Построение графика плотности вероятности, проверка гипотезы о законе распределения
Во многих случаях желательно построить график кривой плотности вероятности того или иного закона распределения и совместить его с гистограммой, что позволяет наглядно оценить степень их сходства. В процессе расчета точек кривой можно получить количественные меры соответствия фактической гистограммы теоретическому закону распределения случайной величины. Рассмотрим построение кривой плотности вероятности нормального закона на примере данных табл.2.4 и рис.2.1. Чтобы построить кривую, необходимо рассчитать значения функции f (t) по формуле (2.22) и нанести их на график. Имеет смысл рассчитать лишь те значения, которые соответствуют серединам классов гистограммы. Расчет выполнен по форме табл.2.13, в которой первые семь граф заимствованы из табл.2.5. Они нужны для расчета статистических характеристик. Для построения кривой достаточно иметь две характеристики: среднее значение и дисперсию. В качестве аргумента можно брать номера классов у, что значительно упрощает расчеты. В результате вычислений получены
Зная t, можно рассчитать плотность вероятности f (t) либо по табл.2.6, либо по формуле (2.22). Все необходимые расчеты выполнены в табл.2.13.
Таблица 2.13
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 687; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.197.189 (0.009 с.) |

 = 2,2 и s = 0,40. По формуле (2.24) вычислим нормированные значения t 1 = (2,72 – 2,2)/0,40 = 1,31; t 2 = (2,96 – 2,2)/0,40 = 1,90. В табл.2.6 найдем вероятности F (t 1) = 0,9032; F (t 2) = 0,9713. Отсюда имеем вероятность попадания случайной величины в заданный интервал q = F (t 2) – F (t 1) = 0,0681.
= 2,2 и s = 0,40. По формуле (2.24) вычислим нормированные значения t 1 = (2,72 – 2,2)/0,40 = 1,31; t 2 = (2,96 – 2,2)/0,40 = 1,90. В табл.2.6 найдем вероятности F (t 1) = 0,9032; F (t 2) = 0,9713. Отсюда имеем вероятность попадания случайной величины в заданный интервал q = F (t 2) – F (t 1) = 0,0681.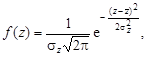 (2.28)
(2.28) – среднее значение логарифмов; s – среднеквадратичное отклонение логарифмов.
– среднее значение логарифмов; s – среднеквадратичное отклонение логарифмов.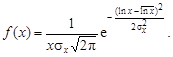 (2.29)
(2.29) График функции f (х) асимметричен (рис.2.9), среднее значение, мода и медиана не совпадают между собой. Они связаны с величинами
График функции f (х) асимметричен (рис.2.9), среднее значение, мода и медиана не совпадают между собой. Они связаны с величинами 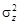 следующими соотношениями:
следующими соотношениями: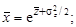
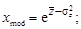
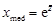 . (2.30)
. (2.30)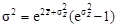 . (2.31)
. (2.31)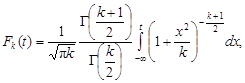 (2.32)
(2.32)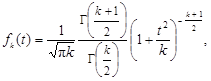 (2.33)
(2.33)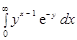 . (2.34)
. (2.34)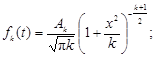
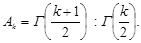

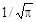 , и далее пользоваться рекуррентной формулой Аk + 1 = k /2 Ak. Так, А 2 =
, и далее пользоваться рекуррентной формулой Аk + 1 = k /2 Ak. Так, А 2 = 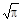 /2, А 3 = 2/
/2, А 3 = 2/ 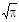 и т.д. Некоторые значения плотности вероятности приведены в табл.2.9. Последняя графа соответствует нормальному распределению.
и т.д. Некоторые значения плотности вероятности приведены в табл.2.9. Последняя графа соответствует нормальному распределению.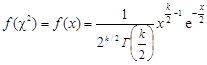 , (2.35)
, (2.35)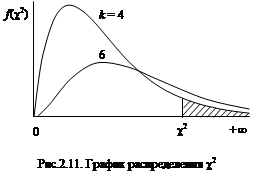 Случайная величина c2 имеет область существования от нуля до +¥. График плотности вероятности асимметричен (рис.2.11), модальное значение
Случайная величина c2 имеет область существования от нуля до +¥. График плотности вероятности асимметричен (рис.2.11), модальное значение 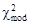 = k – 2.
= k – 2.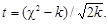 (2.36)
(2.36)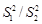 , причем в числитель отношения всегда помещают бόльшую дисперсию, т.е.
, причем в числитель отношения всегда помещают бόльшую дисперсию, т.е. 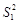 >
> 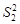 . Плотность вероятности распределения величины F выражается формулой
. Плотность вероятности распределения величины F выражается формулой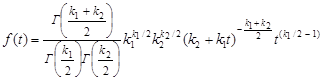 , (2.37)
, (2.37)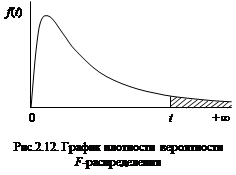
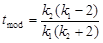 . (2.38)
. (2.38)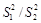 превысит некоторое критическое значение t. Если отношение
превысит некоторое критическое значение t. Если отношение 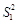 = = 5,22 и
= = 5,22 и 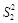 = 1,86. Число измерений соответственно n 1 = 16, n 2 = 31.
= 1,86. Число измерений соответственно n 1 = 16, n 2 = 31.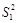 и
и 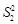 различаются между собой с вероятностью более p = 1 – 0,05 = = 0,95.7
различаются между собой с вероятностью более p = 1 – 0,05 = = 0,95.7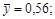
 = 6,40; s у = 2,53. Далее по формуле (2.24) нужно перейти от условной величины у к нормированной величине t:
= 6,40; s у = 2,53. Далее по формуле (2.24) нужно перейти от условной величины у к нормированной величине t: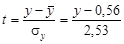 .
.


