Пример экспериментальных данных описан в научно-популярном журнале. В начале ХХ в. немецкий физик Отто Ган, измеряя импульсы от препарата урана, облученного нейтронами, установил тенденцию уменьшения числа распадов с течением времени (табл.3.7, рис.3.11).
Взяв за аргумент среднее время в интервале измерения, а за функцию – число распадов атомов в минуту, можно определить постоянную распада l и период полураспада T. Уравнение (3.38) предварительно прологарифмируем и приведем к линейному виду:
ln y = ln y 0 – l t. (3.39)
|
Найдем линейную зависимость ln у от t. В результате вычислений по данным табл.3.7 получим уравнение линейной регрессии ln у = 4,1006 – 0,00442 t. Потенцируя его, найдем искомую зависимость у = 60,38е–0,0044. Значения у расч, вычисленные по этой формуле, приведены в табл.3.7 и по ним построена плавная кривая на рис.3.11. Заметный разброс точек относительно линии обусловлен тем, что распад атомов происходит неравномерно во времени.
Таким образом, постоянная распада l = 0,00442. Период полураспада T = ln(2)/0,00442 = 157 мин = 2 ч 37 мин. Эти данные позволили Отто Гану установить, что импульсы создаются не ураном или радием, периоды полураспада которых были уже известны, а каким-то другим химическим элементом (изотопом). Дальнейшими исследованиями было установлено, что атом урана распадается на два осколка – на атомы бария и криптона. Так эксперимент перерос в крупное научное открытие явления искусственного распада атомного ядра.
3.2.7. Зависимость плотности руды от ее состава
Плотность многих видов полезных ископаемых зависит от их состава. Так, плотность железной руды зависит от содержания в ней железа, сульфидной руды – от содержания серы и т.д. Как показано в подразделе 1.2.2, данная зависимость является гиперболической, хотя часто приближается к линейной.
Рассматриваемая зависимость позволяет решать две задачи: 1) определять плотность руды при известном ее составе, что используется для подсчета запасов; 2) определять состав руды по ее плотности, что применяется при геофизическом опробовании руд.
8 Пример 3.6. Известны плотность железной руды y и содержание в ней железа х (табл.3.8). Необходимо рассчитать зависимость между этими величинами.
Теоретическое уравнение зависимости выражается гиперболой (1.5). Преобразуем уравнение к линейному виду a + bxy = y, как в подразделе 3.1.8. Вычисление уравнения регрессии дает коэффициенты a = 2,722, b = 0,00655. Следовательно, уравнение зависимости имеет вид
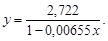
Вычисленные по уравнению расчетные значения плотности у расч близки к фактическим. Дисперсия отклонений фактических значений от расчетных 
= 0,006556, дисперсия фактических значений 
= 0,2541. Отсюда получены дисперсия тренда 
= 0,2475 и корреляционное отношение h = 0,987.
Таблица 3.8
Содержание железа в руде и плотность руды
| Номер пробы n | Содер- жание железа x, % | Плотность, т/м3 | Номер пробы n | Содер-жание железа x, % | Плотность, т/м3 | ||
| фактическая y | расчетная у расч | фактическая y | расчетная у расч | ||||
| 41,33 | 3,77 | 3,73 | 34,00 | 3,57 | 3,50 | ||
| 64,00 | 4,71 | 4,69 | 40,05 | 3,66 | 3,69 | ||
| 64,78 | 4,79 | 4,73 | 62,46 | 4,63 | 4,61 | ||
| 57,58 | 4,25 | 4,37 | 20,18 | 3,16 | 3,14 | ||
| 27,63 | 3,34 | 3,32 | 44,28 | 3,82 | 3,83 | ||
| 32,14 | 3,59 | 3,45 | 26,77 | 3,22 | 3,30 | ||
| 54,38 | 4,07 | 4,23 | 39,34 | 3,63 | 3,67 | ||
| 49,66 | 4,14 | 4,03 | 43,19 | 3,65 | 3,80 | ||
| 25,13 | 3,36 | 3,26 | 50,16 | 3,96 | 4,05 | ||
| 46,06 | 3,84 | 3,90 | 26,21 | 3,16 | 3,29 | ||
| 52,83 | 4,11 | 4,16 | 38,10 | 3,64 | 3,63 | ||
| 49,98 | 4,20 | 4,05 | 27,96 | 3,34 | 3,33 | ||
| 62,36 | 4,65 | 4,60 | 62,78 | 4,68 | 4,62 | ||
| 30,58 | 3,49 | 3,40 | 20,78 | 3,11 | 3,15 | ||
| 61,82 | 4,54 | 4,57 | 24,05 | 3,25 | 3,23 | ||
| 34,34 | 3,58 | 3,51 | 38,98 | 3,58 | 3,63 |
Из уравнения зависимости можно извлечь дополнительную геологическую информацию. При отсутствии рудного минерала (магнетита) содержание железа в нерудных минералах близко к 10 %. Подставив это значение в формулу зависимости, получим плотность суммы нерудных минералов 2,91 т/м3. Если же взять чистый магнетит, в котором за счет примесей содержание железа несколько ниже теоретического и близко к 71,5 %, то плотность магнетита составит 5,12 т/м3.7
3.2.8. Вычисление параметров усеченного нормального
распределения
В ряде случаев гистограмма искусственно ограничена (обычно слева) пределом точности анализа или кондициями. Необходимо восстановить параметры распределения по усеченной гистограмме. Такая задача может быть решена, если известен или предполагается закон распределения случайной величины. Для решения применяется разновидность метода наименьших квадратов со взвешиванием наблюдений. Суть метода состоит в том, что классы гистограммы имеют различный вес, пропорциональный частоте появления свойства в данном классе. Запись метода наименьших квадратов в данном случае имеет вид
(3.40)
где pi – весовые коэффициенты.
В случае нормального закона распределения характеристики усеченного распределения находят следующим образом. Уравнение кривой, аппроксимирующей гистограмму, имеет вид
(3.41)
где n – теоретические частоты; N – общее количество наблюдений, которое неизвестно (гистограмма обрезана); h – размер классов.
Необходимо определить характеристики полного распределения: среднее значение 
, дисперсию s2 и число наблюдений N, чтобы оценить, какая часть гистограммы отсутствует. Перед применением метода наименьших квадратов функцию (3.41) логарифмируют:
Отклонения для такой функции имеют вид
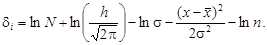(3.42)
В качестве весов наблюдений берется частота свойств в классах гистограммы. Чем больше n, тем весомее роль класса. Следовательно, сумма квадратов отклонений является функцией неизвестных величин , s и N и должна быть минимальной:
(3.43)
где k – число имеющихся классов гистограммы.
Чтобы найти минимум суммы квадратов, нужно взять частные производные от выражения (3.43) по каждой из неизвестных величин и приравнять их нулю, в результате получим линейную систему уравнений относительно неизвестных , s и N. Опуская громоздкие промежуточные выкладки, приведем порядок вычислений. Вначале находят восемь сумм: S n, S nх, S nх 2, S nх 3, S nх 4, S n ln n, S nx ln n, S nx 2ln n (индекс i опущен). Разделив каждую сумму на S n, получим семь начальных моментов: m 10, m 20, m 30, m 40, m 01, m 11 и m 21 соответственно. Далее вычислим вспомогательные величины:
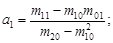
И, наконец, искомые величины:
В заключение нужно учесть размер класса, умножив s2 на h 2,а на h, чтобы иметь статистические характеристики в истинном масштабе. Для достаточно надежного определения статистических характеристик нужно иметь не менее 2/3 классов гистограммы, включая классы с максимальной частотой.
|
8 Пример 3.7. Имеется неполная гистограмма (рис.3.12, табл.3.9). Размер классов h = 1. Необходимо рассчитать недостающие частоты и достроить кривую нормального распределения.
В ходе расчетов последовательно получены суммы: S n = 195; S nx = 696; S nx 2 = 3154; S nx 3 = 16554; S nx 4 = 95590; S n ln n = 649,255; S nx ln n = 2206,209; S nx 2ln n = 9416,719.
Таблица 3.9
Расчет частот n
| Класс х, % | Частоты | Класс х, % | Частоты | |||||
| фактические | расчетные | округленные | фактические | расчетные | округленные | |||
| 14-15 | – | 0,1 | – | 24-25 | 34,2 | |||
| 15-16 | – | 0,3 | – | 25-26 | 26,6 | |||
| 16-17 | – | 1,0 | 26-27 | 17,8 | ||||
| 17-18 | – | 2,7 | 27-28 | 10,2 | ||||
| 18-19 | – | 6,2 | 28-29 | 5,0 | ||||
| 19-20 | – | 12,0 | 29-30 | – | 2,1 | |||
| 20-21 | – | 20,1 | 30-31 | – | 0,8 | |||
| 21-22 | 28,9 | 31-32 | – | 0,2 | – | |||
| 22-23 | 35,6 | 32-33 | – | 0,1 | – | |||
| 23-24 | 37,6 | |||||||
| Cумма | 241,5 | |||||||
После деления сумм на S n найдем моменты: m 10 = 3,5692307; m 20 = 16,17436; m 30 = 84,89231; m 40 = 490,20512; m 01 = 3,329513; m 11 = 11,31389; m 21 = 48,29086. Далее вычисляем вспомогательные величины: a 1 = –0,1659145; a 2 = –0,2047645; b 1 = 8,415905; b 2 = 7,907624. Зная их, определим характеристики распределения: 
= 6,5416; s х = 2,5577; = 2,8685; ln N = 5,4876; N = e5,4876 = 241,68. Промежуточные расчеты полезно выполнять без округления, иначе при нахождении многочисленных разностей, имеющихся в формулах, точность расчетов заметно снизится.
Так как округленно N = 242, то полная гистограмма должна содержать 242 значения, фактически же имеется 195, следовательно, не хватает 47 значений. Чтобы узнать, в каких классах они должны быть, нужно найти расчетные частоты по формуле (3.41) и сравнить их с фактическими (табл.3.9). По расчетным значениям построена кривая частот нормального закона (рис.3.12), которая хорошо аппроксимирует гистограмму.
МНОГОМЕРНАЯ
СТАТИСТИЧЕСКАЯ МОДЕЛЬ
И ЕЕ ПРИМЕНЕНИЕ В ГЕОЛОГИИ
Глава
|
| Поделиться: |
