8 Пример 5.6. Имеются результаты измерения переменной (табл.5.4). Требуется рассчитать наилучший полиномиальный тренд.
|
Для оценки математического ожидания выберем полином, рассчитанный по методу наименьших квадратов. Оптимальный порядок полинома определим по методике, описанной в подразделе 3.1.7. Наилучшим оказался полином третьего порядка. Его уравнение имеет вид
m (х) = 0,05178 + 1,41332 х – 0,018784 х 2 + 0,0000055 х 3.
После вычитания из исходных данных полинома получим остаток – случайные отклонения, которые колеблются около оси абсцисс (рис.5.9). Дисперсия случайных отклонений с учетом использованных степеней свободы D = 0,447026.7
На практике часто используют двухмерный (площадной) тренд, который аппроксимируют двухмерным полиномом невысокого порядка (не более третьего), хотя теоретически можно использовать методику отыскания наилучшего порядка полинома. Тренды высокого порядка требуют большого объема вычислений и часто дают нереальные значения между пунктами измерений.
8 Пример 5.7. Имеются данные по опробованию штокверка молибденового месторождения на одном из горизонтов (табл.5.5). Требуется построить тренд содержания молибдена.
Таблица 5.5
Содержание молибдена, %
| Номер пункта | ||||||||||||
| 0,12 | 0,04 | 0,10 | 0,13 | 0,11 | 0,17 | 0,14 | 0,32 | 0,66 | 0,28 | 0,25 | 0,33 | |
| 0,15 | 0,51 | 0,19 | 0,09 | 0,09 | 0,20 | 0,21 | 0,31 | 0,35 | 0,32 | 0,26 | 0,35 | |
| 0,07 | 0,54 | 0,27 | 0,17 | 0,11 | 0,16 | 0,42 | 0,67 | 0,23 | 0,35 | 0,29 | 0,28 | |
| 0,22 | 0,34 | 0,24 | 0,25 | 0,07 | 0,20 | 0,44 | 0,46 | 0,24 | 0,36 | 0,24 | 0,27 | |
| 0,21 | 0,28 | 0,37 | 0,18 | 0,13 | 0,22 | 0,57 | 0,48 | 0,20 | 0,28 | 0,25 | 0,25 | |
| 0,10 | 0,15 | 0,17 | 0,20 | 0,30 | 0,15 | 0,50 | 0,43 | 0,41 | 0,66 | 0,41 | 0,33 | |
| 0,15 | 0,08 | 0,13 | 0,25 | 0,64 | 0,21 | 0,16 | 0,19 | 0,34 | 0,62 | 0,44 | 0,36 | |
| 0,78 | 0,17 | 0,14 | 0,19 | 0,25 | 0,40 | 0,27 | 0,21 | 0,23 | 0,58 | 0,54 | 0,33 | |
| 0,58 | 0,57 | 0,17 | 0,20 | 0,28 | 0,64 | 0,77 | 0,23 | 0,23 | 0,33 | 0,43 | 0,51 | |
| 0,27 | 0,22 | 0,19 | 0,21 | 0,25 | 0,26 | 0,42 | 0,42 | 0,24 | 0,34 | 0,37 | 0,49 |
|
Обозначим ось абсцисс х, ось ординат y. Для тренда применим двухмерный полином третьего порядка:
m (х, у) = a 0 + a 1 x + a 2 y +
+ a 3 x 2 + a 4 xy + a 5 y 2 + a 6 x 3 +
+ a 7 x 2 y + a 8 xy 2 + a 9 y 3.
Вычислим тренд методом наименьших квадратов. В результате расчета найдем коэффициенты тренда:
а 0 = 0,504237;
а 1 = –0,130796;
а 2 = –0,0669908;
а 3 = 0,0279553;
а 4 = 0,00381132; а 5 = 0,0108503;
а 6 = –0,0014979; а 7 = –0,000349273;
а 8 = 0,0000063219; а 9 = –0,000772421.
Используя коэффициенты, построим график, характеризующий тренд содержания молибдена на горизонте (рис.5.10).7
Еще один способ приближенной оценки математического ожидания основан на методе сглаживания исходных данных с помощью скользящего окна. Его часто называют сглаживающим фильтром и используют для выделения полезного сигнала на фоне случайных помех. По существу, сглаженные данные характеризуют не математическое ожидание, а тенденцию изменения пространственной переменной. Сглаживание – простая операция, не требующая больших вычислений. Существует много способов сглаживания. Наиболее часто сглаживание осуществляется скользящим окном, содержащим три соседних наблюдения. По этим трем наблюдениям находят среднеарифметическое значение, которое сопоставляют с серединой окна. Потом окно передвигают на одно наблюдение, расчет повторяют и так поступают до конца ряда измерений.
Могут быть использованы окна с различным нечетным числом измерений. Роль измерений в окне также может быть различной – центральным значениям чаще придают бóльший вес. В случае значительного разброса исходных данных хороший результат дает медианное сглаживание, когда в окне в качестве среднего значения используют медиану.
8 Пример 5.8. Имеются исходные данные из 20 измерений (табл.5.6). Требуется выполнить сглаживание данных.
Таблица 5.6
Сглаживание исходных данных
| Номер пункта | Исходные данные | Первое сглаживание | Второе сглаживание | Третье сглаживание | |||||
| x | f (x) | f 1 | δ1 | f 2 | d2 | f 3 | d3 | ||
| 8,6 | 9,5 | 10,2 | 0,7 | 11,0 | 1,5 | 11,4 | 1,9 | ||
| 9,8 | 11,6 | 12,5 | 0,9 | 12,3 | 0,7 | 12,8 | 1,2 | ||
| 11,5 | 16,3 | 14,2 | –2,1 | 15,1 | –1,2 | 15,0 | –1,3 | ||
| 13,8 | 14,8 | 18,7 | 3,9 | 17,6 | 2,8 | 17,7 | 2,9 | ||
| 20,0 | 25,0 | 19,9 | –5,1 | 20,5 | –4,5 | 20,1 | –4,9 | ||
| 24,0 | 19,8 | 22,9 | 3,1 | 22,3 | 2,5 | 22,5 | 2,7 | ||
| 25,5 | 24,0 | 24,1 | 0,1 | 24,6 | 0,6 | 24,5 | 0,5 | ||
| 29,2 | 28,5 | 26,8 | –1,7 | 26,7 | –1,8 | 26,8 | –1,7 | ||
| 35,8 | 28,0 | 29,3 | 1,3 | 29,0 | 1,0 | 28,7 | 0,7 | ||
| 43,8 | 31,4 | 30,9 | –0,5 | 30,4 | –1,0 | 30,1 | –1,3 | ||
| 50,5 | 33,4 | 30,9 | –2,5 | 31,0 | –2,4 | 30,5 | –2,9 | ||
| 55,2 | 27,9 | 31,1 | 3,2 | 30,0 | 2,1 | 29,9 | 2,0 | ||
| 61,5 | 32,1 | 28,0 | –4,1 | 28,8 | –3,3 | 28,8 | –3,3 | ||
| 62,5 | 24,0 | 27,4 | 3,4 | 27,5 | 3,5 | 27,8 | 3,8 | ||
| 63,9 | 26,0 | 27,0 | 1,0 | 27,0 | 1,0 | 26,9 | 0,9 | ||
| 69,2 | 31,0 | 26,7 | –4,3 | 26,1 | –4,9 | 26,1 | –4,9 | ||
| 73,1 | 23,2 | 24,6 | 1,4 | 24,3 | 1,1 | 24,1 | 0,9 | ||
| 79,6 | 19,5 | 21,6 | 2,1 | 21,8 | 2,3 | 21,9 | 2,4 | ||
| 82,2 | 22,1 | 19,1 | –3,0 | 19,5 | –2,6 | 19,9 | –2,2 | ||
| 87,7 | 15,8 | 17,9 | 2,1 | 18,3 | 2,5 | 18,7 | 2,9 | ||
| Дисперсия | 45,9 | - | 7,28 | - | 6,10 | - | 6,71 | ||
Для сглаживания выберем окно размером в три измерения. Возьмем первые три значения f (x)и вычислим среднее значение:
получим сглаженное значение во второй строке таблицы. Переместим окно на одно измерение и вычислим следующее значение:
|
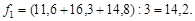
Продолжая перемещать окно, аналогично найдем остальные сглаженные значения. Исключение составляют крайние сглаженные значения, при расчете которых крайние значения используются дважды.
Когда первое сглаживание закончено, рассчитаны отклонения сглаженных значений от исходных значений d1 и найдена дисперсия отклонений (7,28), можно выполнить второе сглаживание и снова найти отклонения сглаженных значений от исходных значений f (x), а также дисперсию отклонений (6,10). Сглаживание повторяется и оканчивается после достижения минимума дисперсии отклонений. В данном примере минимум дисперсии достигнут после второго сглаживания (табл.5.5). На рис.5.11 совмещены исходные и сглаженные значения.7
5.4.2. Гармонический анализ
Как упоминалось выше, в составе закономерной изменчивости часто присутствует периодическая составляющая. Ее можно выделить и вычесть из исходных данных с помощью гармонического или периодограммного анализа. Гармонический анализ позволяет ряд исходных данных представить как сумму синусоид. Но здесь, в отличие от классического гармонического анализа, необходимо выделить наиболее существенные синусоиды, которые вносят основной вклад в изменчивость пространственной переменной.
Периодические явления широко распространены в природе, они находят свое выражение в ритмичном напластовании горных пород, в развитии систем упорядоченных трещин, в формировании рудных столбов. Чтобы выявить и охарактеризовать периодичность, необходимо применить специальные математические приемы.
Предлагаемая методика характеризуется тем, что в ряду наблюдений последовательно находят синусоиды в порядке убывания их значимости и вычитают из исходных данных. Можно извлечь несколько (иногда одну) важнейших синусоид и этим ограничиться. Но можно извлекать синусоиды до тех пор, пока дисперсия отклонений суммы синусоид от исходных данных с учетом использованных степеней свободы не будет минимальной.
Каждая синусоида имеет три характеристики: амплитуду А, длину волны L (или обратную ей величину – частоту) и начальную фазу y, поэтому каждая синусоида использует три степени свободы. Кроме того, часто находят дисперсию синусоиды, которая пропорциональна квадрату амплитуды. Ряд значений пространственной переменной f (х) представляют в виде суммы N гармоник (синусоид) w k (x):
f (х) = 
, (5.13)
где 
– свободный член, равный среднеарифметическому значению пространственной переменной.
В качестве первой длины волны L чаще всего принимается длина ряда наблюдений. Каждая гармоника w k (x) выражается формулой
(5.14)
или в другой форме записи:
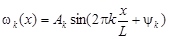. (5.15)
Здесь ak, bk – коэффициенты; k – номер гармоники (синусоиды); L / k – длина волны; Ak – амплитуда; y k – начальная фаза гармоники; k = 1, 2, …, N.
Амплитуда и начальная фаза связаны с коэффициентами ak, bk соотношениями
. (5.16)
Количество гармоник N может быть большим, но на практике принимается конечным. Количество гармоник не должно превышать n /2 (где n – количество измерений), но наиболее правильно ограничивать их количество по минимальной дисперсии отклонений с учетом степеней свободы, как в подразделе 3.1.7 или 4.1.3. Каждая синусоида использует три степени свободы, поэтому k синусоид поглощают 3 k степеней свободы. Впрочем, для геологических целей обычно выбирают одну или две важнейшие синусоиды, пренебрегая остальными. За счет ограничения количества синусоид их сумма в формуле (5.13) приближенно равна пространственной переменной f (х).
Объединение формул (5.13) и (5.14) дает ряд Фурье (гармонический ряд):
f (х) = 
. (5.17)
Коэффициенты ak, bk находят по формулам
); (5.18)
. (5.19)
Когда коэффициенты ak и bk определены, вычисляют амплитуды гармоник по формуле (5.16). Совокупность всех гармоник образует спектр амплитуд. Чем больше амплитуда, тем бόльшую роль играет соответствующая гармоника. Для количественной оценки роли гармоник используют их дисперсии Dk, совокупность которых составляет спектр дисперсий. Сумма дисперсий всех гармоник равна дисперсии пространственной переменной, что позволяет оценить роль каждой гармоники в абсолютных или относительных единицах. Вычисление дисперсии любой гармоники лучше всего осуществлять путем сравнения остаточных дисперсий до вычитания и после вычитания гармоники из значений пространственной переменной. Уменьшение остаточной дисперсии характеризует дисперсию Dk, поглощенную данной гармоникой.
8 Пример 5.9. Имеются результаты 25 измерений пространственной переменной f (x) – содержаний цинка в скважинепо сети с шагом 1 м (табл.5.7). Очевидно, что длина отрезка (начальная длина волны) L = 25 – 1 = 24 м. Необходимо разложить пространственную переменную в ряд Фурье и оценить роль различных гармоник.
Задачу решим путем последовательного вычисления и вычитания гармоник из значений пространственной переменной (кстати, наиболее рациональный метод при неравномерной сети наблюдений). Вначале из значений пространственной переменной вычтем свободный член ряда (5.17), что даст отклонения d0(х) = f (x) – a 0/2. Далее из отклонений d0(х) вычтем первую гармонику w1(х), что даст остаток d1(х). Из него вычтем вторую гармонику и этот процесс продолжим до заданного числа гармоник N = 12. Начало вычислений, включая первые две гармоники, показано в табл.5.7. Коэффициенты ak и bk каждой очередной гармоники найдем через отклонения d(х) по преобразованным формулам (5.18) и (5.19):
; (5.20)
, (5.21)
где 
– вспомогательный аргумент, вводимый для сокращения вычислений.
Таблица 5.7
|
| Поделиться: |
