
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двухмерная статистическая модельСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
3.1.1. Система двух случайных величин и ее графическое изображение Во многих геологических задачах изучают два взаимосвязанных свойства множества геологических объектов. Такой анализ проводится на основе двухмерной статистической модели. Пусть имеется система из n однородных геологических объектов, у каждого из них измерены характеристики двух свойств. Результаты измерений одного свойства обозначим х 1, х 2, …, хn, второго свойства у 1, у 2, …, уn. Их можно записать в виде таблицы-матрицы (1.1), в которой число строк равно n, а число столбцов k = 2. В основе двухмерной модели лежат те же гипотезы, что и в основе одномерной: а) значения х 1, х 2, …, хn, у 1, у 2, …, уn носят случайный характер; б) значения первого свойства х 1, х 2, …, хn не зависят между собой, значения второго свойства у 1, у 2, …, уn также не зависят между собой (но могут существовать зависимости между свойствами х и у); в) совокупность измеренных свойств является однородной. Система значений х 1, х 2, …, хn, у 1, у 2, …, уn называется системой двух случайных величин, двухмерной случайной величиной или случайным вектором. Результаты измерений двухмерной случайной величины принято изображать на графике, где по оси абсцисс откладывают характеристику одного свойства, а по оси ординат – другого. Каждый геологический объект на таком графике изображают точкой, а множество объектов – облаком точек (рис.3.1). Расположение точек на графике позволяет сделать предварительные выводы о характере зависимости между свойствами. Если точки расположены вдоль линии (рис.3.1, а, б), то между характеристиками свойств имеется функциональная зависимость. Она может быть линейной и нелинейной. Если же точки расположены беспорядочно (рис.3.1, в), то зависимости между характеристиками свойств нет. Чаще всего точки располагаются в виде облака, группирующегося вдоль какой-то линии (рис.3.1, г, д), в этом случае наблюдается нестрогая статистическая зависимость между свойствами. Она также может быть линейной и нелинейной. Функциональные и статистические зависимости могут быть положительными, когда с возрастанием характеристики одного свойства увеличивается и другая (рис.3.1, а, г), но могут быть и отрицательными, когда характеристика одного свойства растет, а другого убывает (рис.3.1, б, д). Иногда точки могут образовать два и более изолированных или частично перекрывающихся облака (рис.3.1, е), что свидетельствует о двух и более однородных совокупностях, которые следует изучать раздельно.
3.1.2. Статистические характеристики системы двух случайных величин. Коэффициент корреляции
Система двух случайных величин имеет пять основных статистических характеристик: средние значения Первые четыре формулы встречались ранее. Особый интерес представляет пятая формула, которая отражает взаимосвязь между случайными величинами х и у. Поскольку корреляционный момент имеет размерность, его преобразуют в безразмерную величину по формуле Величина r играет чрезвычайно большую роль в статистических исследованиях и называется коэффициентом корреляции. Его значения заключены в интервале между +1 и –1. Если коэффициент корреляции равен нулю, то линейная связь между случайными величинами отсутствует (рис.3.1, в). При r = 1 связь функциональная положительная (см. рис.3.1, а). При r = –1 связь функциональная отрицательная (см. рис.3.1, б). В реальных условиях коэффициент корреляции не бывает равен единице (или минус единице) и характеризует степень статистической связи между свойствами х и у. Чем ближе по абсолютной величине r к единице, тем сильнее связь между свойствами; она может быть положительной (r > 0) и отрицательной (r < 0). Таким образом, коэффициент корреляции является мерой линейной зависимости между двумя величинами. Для оценки нелинейных зависимостей он непригоден. На вычисленную величину r в заметно влияет случайная погрешность измерений исходных данных, уменьшая истинное значение коэффициента корреляции r: где Влияние погрешности может оказаться настолько значительным, что зависимость между случайными величинами не будет выявлена. Статистическая линейная связь между характеристиками двух свойств считается доказанной, если критерий t будет больше предельного t доп. Коэффициент корреляции, при котором связь считается доказанной, называется значимым коэффициентом корреляции. Для установления значимости используется критерий t, основанный на распределении Стьюдента с числом степеней свободы k = n – 2:
где Sr – оценка среднеквадратичного отклонения коэффициента корреляции. Если критерий t будет больше допустимого t доп при заданной вероятности b (см. табл.2.10), то связь считается доказанной. Имеет смысл принять вероятность b = 0,0027, что соответствует правилу «трех сигм». При большом значении n можно пользоваться более простым критерием, основанным на нормальном законе распределения:
Если t > 3 (что соответствует вероятности b = 0,0027), то связь считается доказанной. Еще один критерий предложен Фишером:
где z – новая переменная, полученная преобразованием коэффициента корреляции через гиперболический арктангенс, И здесь для доказательства связи необходимо выполнение условия t > 3. Из соотношения (3.6) выводится формула значимого коэффициента корреляции Так как t доп зависит от числа наблюдений (точнее, от числа степеней свободы k = n – 2), то и значимый коэффициент корреляции зависит от числа наблюдений. При увеличении числа наблюдений, как следует из соотношения (3.7), формула (3.10) упрощается: Обычно принимается значение t доп = 3.
8 Пример 3.1. Известны содержания общего и магнетитового железа в руде. Требуется рассчитать коэффициент корреляции между этими величинами (табл.3.1). Таблица 3.1
|
|||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 678; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |


 и
и  , дисперсии
, дисперсии  и
и  и корреляционный момент (или ковариацию) Kху, которые вычисляют по формулам:
и корреляционный момент (или ковариацию) Kху, которые вычисляют по формулам:
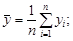 (3.1)
(3.1)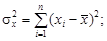
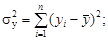 (3.2)
(3.2)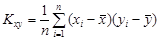 . (3.3)
. (3.3)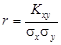 . (3.4)
. (3.4)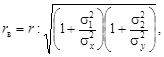 (3.5)
(3.5)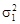 и
и 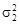 – дисперсии случайной погрешности измерений величин х и у соответственно.
– дисперсии случайной погрешности измерений величин х и у соответственно.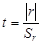 при
при 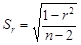 , (3.6)
, (3.6)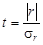 при
при 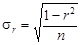 . (3.7)
. (3.7)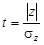 при
при 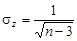 , (3.8)
, (3.8)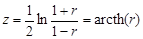 . (3.9)
. (3.9)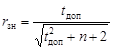 . (3.10)
. (3.10)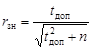 . (3.11)
. (3.11)


