
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Результаты расчета всех гармоникСодержание книги
Поиск на нашем сайте
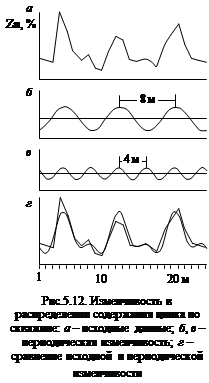
Коэффициенты ak и bk позволяют рассчитать амплитуды всех гармоник по формуле (5.16), а отклонения – их дисперсии по формуле (5.22). Результаты расчетов по всем 12 гармоникам суммированы в табл.5.8. Отметим, что отношение L / k – это длина волны гармоники k. В таблице приведены длина волны, коэффициенты ak и bk, амплитуда А, дисперсии отклонений D (o, k), их разности – дисперсии гармоник D (k) и они же, выраженные в процентах от дисперсии пространственной переменной. Вычисления показали, что главное значение имеют третья гармоника с длиной волны 8 м (рис.5.12, б), ее доля составляет 62,8 %, и шестая гармоника с длиной волны 4 м (рис.5.12, в), ее доля 20,7 %. Остальные гармоники играют малую роль. Следовательно, можно ограничиться двумя важнейшими гармониками, которые в сумме дают 83,5 % от дисперсии пространственной переменной (рис.5.12, г). Данные табл.5.8 позволяют построить спектр амплитуд (рис.5.13).7
5.4.3. Периодограммный анализ
Периодическая изменчивость не обязательно должна быть синусоидальной, она может иметь любую форму. Можно выявить периодическую изменчивость любой формы путем последовательного перебора длин волн, кратных шагу наблюдений. Такая методика, по-видимому, не описана в литературе. Предлагается назвать ее периодограммным анализом.
Если имеется ряд значений пространственной переменной f (x), измеренных с шагом h, имеющих дисперсию D, то, задавая длину волны, можно выявить периодическую изменчивость w(х) при данной длине волны и вычесть ее из исходных данных, что дает отклонение d(х) = f (x) – w(х). Разность дисперсии исходных данных и дисперсии отклонений дает дисперсию, поглощенную периодической изменчивостью. Чем больше поглощенная дисперсия, тем сильнее проявлена периодическая изменчивость. Задавая различную длину волны, можно найти наибольшую дисперсию, что и лежит в основе периодограммного анализа.
Отыскание наилучшей длины волны начинается с наименьшей длины волны L = h. Затем длина волны последовательно увеличивается до достижения половины ряда наблюдений N = n /2.
8 Пример 5.10. Измерения пространственной переменной приведены в табл.5.7. Необходимо рассчитать периодическую изменчивость ряда значений путем перебора различных длин волн. Покажем порядок расчета при длине волны L = 5 м. Исходные данные «разрежем» на части по пять измерений и запишем один под другим в пять столбцов (табл.5.9). Средние по столбцам – это периодическая изменчивость при длине волны L = 5 м. После вычитания из исходных данных периодической изменчивости получим отклонения. Далее рассчитаем их дисперсию и вычтем из дисперсии исходных данных. Подобные расчеты выполнены для всех длин волн от L = 2 до L = 12 (табл.5.10). Наибольшая дисперсия периодической изменчивости 85,1 % установлена для длины волны 8 м.
Наиболее сильно выраженная волна периодической изменчивости, показанная на рис.5.14, имеет следующий вид: {1,91 1,52 3,01 5,92 5,51 3,10 2,17 2,38}. Можно совместить график исходных данных с графиком периодической изменчивости и убедиться в удовлетворительном их совпадении (рис.5.15). Следует отметить, что дисперсия периодической изменчивости в данном случае несколько больше, чем при гармоническом анализе с использованием двух важнейших гармоник.7
ОСНОВЫ ГЕОСТАТИСТИКИ 5.5.1. Вариограмма и ее аппроксимации
В основе геостатистической группы математических моделей лежит гипотеза о том, что случайный результат измерений обусловлен случайным расположением сети наблюдений. При перемещении сети наблюдений результаты измерений будут другие, но сохраняется одна характеристика – средний квадрат разности между результатами измерений на расстоянии h. Это возможно при эргодичном характере пространственной переменной. На основе гипотезы введена вариограмма γ(h) – главная характеристика в геостатистике. Она равна полусумме среднего квадрата разности между результатами измерений при шаге h и выражается формулой (5.4). Следует отметить, что вариограмма тесно связана со случайными функциями. Сумма вариограммы и ковариации (автокорреляционной функции) равна дисперсии исходных данных: γ(h) + K (h) = D. (5.25) График вариограммы зависит от характера дискретности пространственной переменной. Для непрерывных пространственных переменных (например, мощности пласта) вариограмма начинается с нулевой отметки и возрастает до дисперсии исходных данных (рис.5.16). Для дискретных пространственных переменных вариограмма начинается с некоторой величины С (рис.5.17), называемой эффектом самородков, потому что он был вначале установлен на месторождениях золота. Вариограмма имеет радиус влияния R, который идентичен радиусу автокорреляции в случайной функции. За пределами радиуса влияния вариограмма постоянная и равна дисперсии D, т.е. ее влияние отсутствует. Как упоминалось, радиус R является векторной величиной. В изотропных геологических телах по всем направлениям радиус влияния описывает окружность, за пределами которой влияние вариограммы отсутствует. В анизотропных геологических телах значения радиуса R по разным направлениям столь различны, что напоминают восьмерку. В пункте с координатой R вариограмма может иметь горизонтальную касательную и плавно переходить в линию дисперсии. Эмпирическая вариограмма, получаемая на основе дискретных измерений, строится по отдельным точкам и имеет вид ломаной линии (рис.5.18). Чтобы использовать ее для дальнейших вычислений, необходимо выполнить аппроксимацию вариограммы какой-либо теоретической кривой. Вид аппроксимирующей функции определяет вид геостатистической модели. Существует много видов аппроксимирующих функций. Наибольшее распространение получили четыре функции и, соответственно, четыре геостатистические модели. Первая модель линейная. В ней вариограмма аппроксимируется прямой линией (рис.5.19), что нередко близко к действительности. Во второй модели вариограмма аппроксимируется кубическим полиномом, который не имеет общей касательной с линией дисперсии (рис.5.20). Эта модель лучше всего соответствует действительности. Третья модель (сферическая) также аппроксимируется кубическим полиномом, но он имеет горизонтальную касательную при соприкосновении с линией дисперсии (см. рис.5.16 или рис.5.17). Четвертая модель (модель Де-Вийса) характеризуется тем, что шаг вариограммы откладывается в логарифмическом масштабе, а сама вариограмма представляется в виде прямой линии (рис.5.21).
Выбор варианта аппроксимации носит произвольный характер. Наилучшим вариантом можно считать тот, который дает наименьшую дисперсию отклонений эмпирических значений от теоретических.
На вид вариограммы отрицательно влияет периодическая изменчивость свойств пространственной переменной. Вариограмма колеблется около линии дисперсии, создавая так называемый эффект включений. При сильно выраженной периодической изменчивости радиус влияния определяется неточно.
8 Пример 5.11. В горной выработке определено содержание золота через 1 м (табл.5.11, рис.5.22). Требуется построить вариограмму содержаний и аппроксимировать ее какой-либо моделью. Эмпирическая вариограмма, вычисленная по формуле (5.4), показана на рис.5.18. Она содержит 13 точек, т.е. рассчитана до 12-го шага (половина длины ряда наблюдений).
Начальная часть вариограммы (первые четыре точки) расположена практически на одной линии, поэтому для построения теоретической вариограммы используем линейную модель, как на рис.5.19. Уравнение теоретической вариограммы, рассчитанное по четырем точкам, γ(h) = 0,8 h. Радиус автокорреляции R = 2,5 м получен при пересечении линии теоретической вариограммы с линией дисперсии исходных данных D = 2,03.
5.5.2. Влияние на вариограмму геометрической базы измерений
Многие характеристики пространственной переменной зависят от геометрической базы измерений, т.е. от формы, размеров, а в анизотропных телах и от ориентировки области измерений. К таким характеристикам, в первую очередь, относятся дисперсия и вариограмма. Если область, в которой производится измерение, настолько мала, что ее размерами можно пренебречь, то измерение рассматривается как точечное. Характеристики, полученные из таких измерений, рассматриваются как измерения на точечной геометрической базе.
Пусть в геологическом поле имеется множество точек, в каждой из которых пространственная переменная имеет значение f (x). Если геологическое поле разделить на области объемом v и в каждом из них найти среднее из N точечных значений, то получим новую пространственную переменную fv (x):
где p (m) – весовая функция, зависящая от взаимного расположения точек в объеме v. При увеличении размеров геометрической базы происходит усреднение значений пространственной переменной, соответственно, будут меняться некоторые статистические характеристики. При переходе к бесконечному множеству точек в объеме v выражение (5.26) преобразуется в интегральную форму:
Нахождение средних значений fv (x) по точечным значениям f (x) называется регуляризацией (сглаживанием) пространственной переменной в объеме v. Меняя объем v, будем получать различные регуляризованные пространственные переменные, соответственно, будут меняться и их характеристики. Изменение дисперсии по мере увеличения объема v описывается формулой
где D – дисперсия пространственной переменной на точечной базе; N – число точек в объеме v. Вычитаемое в формуле (5.28) представляет собою среднее значение вариограммы, получаемое при всех возможных положениях точек i и j в объеме v. При переходе к бесконечному множеству точек формула (5.28) приобретает интегральный вид:
Из формул (5.28) и (5.29) следует, что по мере увеличения объема v дисперсия пространственной переменной уменьшается. Подобные формулы существуют и для вариограммы: или в интегральной форме Первое слагаемое в этих формулах характеризует среднюю ковариограмму, которая получается как средняя из вариограмм между всеми точками в объеме v, а вычитаемое – в таком же объеме, смещенном на расстояние h. Формулы (5.28)-(5.31) выведены в предположении, что объем v мал по сравнению с объемом изучаемого геологического объекта, иначе сказывается граничный эффект, который можно учесть введением специальной весовой функции – геометрической ковариограммы p (h): где k (х) = 1, когда точка х находится внутри геологического объекта, k (х) = 0, когда точка х находится за его пределами. Геометрический смысл ковариограммы заключается в степени перекрытия двух объемов, смещенных относительно друг друга на расстояние h. С учетом функции p (h) формулы (5.29) и (5.31) приобретают следующий вид: Если вариограмма аппроксимирована каким-либо алгебраическим выражением, т.е. задан вид математической модели, то интегралы во многих случаях могут быть вычислены и заменены соответствующими алгебраическими выражениями.
8 Пример 5.12. Имеются исходные данные по содержанию золота в горной выработке (табл.5.11). Требуется показать изменение дисперсии и вариограммы при увеличении размера проб.
Будем объединять и усреднять исходные данные по два, три и четыре соседних измерения путем сглаживания методом скользящего окна, что аналогично увеличению размеров проб исходных данных v. Количество исходных данных будет уменьшаться. Рассчитаем дисперсию D усредненных данных по формуле (2.2) и вариограмму g(h) по формуле (5.4) по каждому варианту усреднения. Результаты расчета изображены на рис.5.23 и 5.24. На рисунках видно, что при увеличении размера проб дисперсия уменьшается, по сравнению с рис.5.18 убывает также и вариограмма.7
5.5.3. Понятие о кригинге
На основе геостатистических моделей создан новый метод интерполяции результатов между пунктами измерений, который получил название кригинг (крайгинг)в честь автора метода Д.П.Крига [7]. Как показано Д.Матероном [12], кригинг дает минимальную сумму квадратов отклонений прогнозных значений от фактических значений пространственной переменной. Существует несколько видов кригинга. Вначале рассмотрим простейший – точечный кригинг. Пусть имеется область v, в которой произведены измерения пространственной переменной по дискретной сети (рис.5.25). Каждое измерение считаем точечным, т.е. пренебрегаем геометрической базой измерений.
Прогнозное значение находится в результате выполнения ряда последовательных операций: 1. Рассчитывается эмпирическая вариограмма, как на рис.5.18. 2. Осуществляется аппроксимация эмпирической вариограммы теоретической вариограммой (см. рис.5.19-5.21), т.е. выбирается геостатистическая модель. 3. В области с радиусом R рассчитываются все расстояния между пунктами измерений, а также между пунктами измерений и пунктом прогноза. 4. Составляется симметричная система уравнений кригинга следующего вида:
Здесь g12 – значение теоретической вариограммы между пунктами 1 и 2 (учитывается расстояние между этими пунктами); m – количество пунктов, участвующих в расчете (в данном случае m = 5). 5. Решение системы дает весовые коэффициенты p 1, p 2, p 3, …, pm. 6. Сумма весовых коэффициентов должна быть равна единице, для чего все коэффициенты делятся на их сумму. 7. С помощью весовых коэффициентов вычисляется прогнозное значение свойства в пункте Z: где zi – значения свойства в пунктах c 1-го по m -й. Если понадобится вычислить прогнозное значение в следующем пункте, то операции 3-6 придется выполнить снова. Если в пределах радиуса влияния не окажется ни одного пункта измерения, то кригинг нельзя применять. Приходится обращаться к другим методам интерполяции данных, чаще всего используется метод обратных расстояний. Иногда при составлении системы уравнений (5.35) в матрице коэффициентов оказывается много нулей (расстояния между точками больше радиуса автокорреляции). В этом случае система уравнений является несовместимой, т.е. не имеет решения (или имеет много решений). Тогда весовые коэффициенты лучше всего находить путем деления значений D – γ1 z , D – γ2 z , D – γ3 z , ¼, D – γ mz на дисперсию D и потом приводить сумму коэффициентов к единице. У точечного кригинга имеется один недостаток – в окрестностях пунктов измерений касательная к прогнозным значениям ориентирована горизонтально, как в полиномиальной модели (см. рис.5.2). Чтобы устранить этот недостаток, применяется универсальный кригинг – комбинация тренда с кригингом. Вначале вычисляется тренд f (x), потом остаток от тренда и по остатку осуществляется кригинг. Прогнозное значение находится по формуле
В качестве тренда используется аппроксимирующий полином не выше третьего порядка. Использование тренда частично снимает явление анизотропии, что позволяет применять изотропную схему кригинга. Точечный кригинг можно распространить на объем v. Во всех точках объема с помощью кригинга рассчитывают прогнозное значение свойства, а потом находят среднее из всех значений. Если пункты измерений не точечные, а имеют какой-то объем, то при прогнозировании учитывают все точки в этом объеме. Практически все задачи с объемными геометрическими базами решаются путем вычисления определенных интегралов по этим объемам численными методами.
8 Пример 5.13. Нужно провести точечный кригинг, используя схему рис.5.25 и дополнив недостающие данные. Примем изотропную линейную модель, радиус влияния R = 14 м, дисперсию исходных данных D = 0,42. Исходные данные приведены в табл.5.12. Вариограмма для такой модели имеет следующий вид: до 14 м и после 14 м соответственно
Таблица 5.12 Данные для кригинга, м
|
Иначе говоря, до 14 м вариограмма растет по линейному закону, после 14 м имеет постоянное значение.
Проведем вокруг прогнозного пункта Z окружность радиусом 14 м. Только те пункты и соответствующие значения z, которые попадают в окружность, влияют на результат прогноза. Это пять первых пунктов (см. рис.5.25).
Далее нужно рассчитать расстояния между теми пунктами, которые будут участвовать в прогнозе, по координатам, которые имеются в табл.5.12, и по расстояниям найти значения вариограммы (табл.5.13).
Таблица 5.13
Значения вариограммы g(h)
| Номер пункта | Исходные пункты | Прогнозный пункт z | ||||
| 0,4200 | 0,3015 | 0,3651 | 0,4200 | 0,2955 | ||
| 0,4200 | 0,2121 | 0,4200 | 0,4200 | 0,3498 | ||
| 0,3015 | 0,2121 | 0,4200 | 0,3612 | 0,1530 | ||
| 0,3651 | 0,4200 | 0,4200 | 0,4200 | 0,3189 | ||
| 0,4200 | 0,4200 | 0,3612 | 0,4200 | 0,2955 |
Все готово для составления системы уравнений кригинга (5.35):
 .
.
Решение системы уравнений после приведения суммы корней к единице даcт пять весовых коэффициентов:
{0,0752; –0,1659; 0,6647; 0,2268; 0,1993}.
Подставляя их в формулу (5.36), получим
Z = 0,0752·3,3 – 0,1659·3,1 + 0,6647·3,0 +
+ 0,2268·2,6 + 0,1993·2,1 = 2,73 м.
Обращает на себя внимание, что максимальный весовой коэффициент имеет ближайший пункт 3, который «затеняет» пункт 2, у которого весовой коэффициент отрицательный. Остальные коэффициенты уменьшаются по мере удаления от точки Z. Таким образом, на результат кригинга влияет как удаленность пунктов измерений, так и взаимное их расположение.7
ОСНОВЫ МАТЕМАТИЧЕСКОГО
 МОДЕЛИРОВАНИЯ
МОДЕЛИРОВАНИЯ
МЕСТОРОЖДЕНИЙ
 Глава
Глава
6.1. ЗАДАЧИ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ МЕСТОРОЖДЕНИЙ
При разведке месторождений накапливается большое количество информации: геологическая документация разведочных выработок, данные опробования, результаты геофизических, геохимических исследований и др. В дальнейшем информация перерабатывается с целью построения геологических карт, разрезов, погоризонтных планов, проекций рудных тел, подсчета запасов и решения других вопросов. До появления ЭВМ информацию обрабатывали вручную, что приводило к значительным затратам труда и времени. После появления ЭВМ, особенно персональных компьютеров, мощных серверов и сетей, накопление и обработка геологической информации значительно ускорилась, но и сейчас еще ряд технологических операций в разведке месторождений осуществляется вручную.
Одно из первых назначений компьютера при разведке месторождений состоит в накоплении, систематизации, обработке и передаче геологической информации. Но главное направление при разведке месторождений заключается в математическом моделировании месторождений, что позволяет решать вопросы, касающиеся подсчета запасов, определения качества минерального сырья, геолого-экономической оценки месторождений. На базе математического моделирования месторождений можно проектировать горно-добывающие предприятия, планировать и управлять добычей минерального сырья и решать многие другие прикладные задачи.
Существует, по крайней мере, три направления моделирования месторождений: геоинформационное, аналитическое и блочное. Все они имеют между собой много общего.
Геоинформационное моделирование предназначено в основном для моделирования и построения карт любого назначения, в том числе геологических карт земной поверхности и, как частный случай, построения геологических карт месторождений. Существуют специальные пакеты программ для построения карт, такие как ArcInfo, Arcwiev и др. Пакеты позволяют редактировать и преобразовывать полученную информацию, получать «слои» с различной информацией и совмещать их на одном чертеже.
Аналитическое моделирование предназначено для построения геологических карт и разрезов по данным геологической документации разведочных выработок. Для границ всех горных пород и руд путем ряда преобразований рассчитывают координаты в разведочных выработках. Различные способы интерполяции, рассмотренные в предыдущей главе, позволяют строить геологические границы на планах и в разрезах, т.е. делать графическую модель месторождения (или отдельного рудного тела).
Блочное моделирование основано на разделении пространства, в котором находятся рудные тела, на блоки (ячейки) квадратной (на маломощных рудных телах) или кубической (на мощных рудных телах) формы одинакового размера. Разбиение на блоки осуществляется созданием сети параллельных линий и плоскостей. По данным разведочных выработок путем различных способов интерполяции в каждом блоке рассчитывают параметры оруденения (качество руды, ее свойства, достоверность сведений и другие данные). Задав шкалу значений параметров, можно раскрасить блоки различным цветом и получить цветную модель месторождения в виде множества кубиков. Модель можно поворачивать в пространстве, изучая форму рудного тела и качество руд в трех измерениях. Для работы с подобными моделями месторождений создана серия пакетов прикладных программ: Datamine, Micromine и др. С помощью пакетов можно рассчитывать запасы минерального сырья, осуществлять геолого-экономическую оценку месторождений и проектировать рудники.
Во всех направлениях моделирования предусмотрены сбор данных, их систематизация и обработка (моделирование геологических объектов), хранение данных и представление итоговой информации в графическом или табличном виде.
Исходная информация чаще всего накапливается в бумажном виде. Ее необходимо перенести на машинные носители вручную или с помощью различных технических средств. Часть информации можно получить сразу на машинных носителях, например, путем сканирования изображений или текста, с цифровых фотоаппаратов, с аэро- и космических фотоаппаратов, в результате геофизических измерений физических полей и др. Как при ручном наборе информации, так и с применением технических средств исходные данные обычно преобразуются в цифровую или символьную форму и хранятся в виде файлов баз данных в Excel, dBASE, Access, FoxPRO, Paradox, Word, MS DOS и др. База состоит из отдельных банков однородных данных.
Каждая модель или пакет преобразует банки данных в удобную для обработки форму с помощью специальных программ – конвертеров.
6.2. Банки исходных данных при разведке месторождений
6.2.1. Банк координат устьев разведочных выработок
Разведка месторождений ведется по дискретной сети наблюдений с помощью разведочных выработок (скважин, горных выработок) при вспомогательной роли геофизических работ. Все разведочные выработки подвергаются геологической документации и опробованию. В рудных пересечениях и их ближайших окрестностях, как правило, берут пробы для химического, минералогического или технического анализа, чтобы установить границы рудных тел и определить качество полезного ископаемого. Вмещающие породы нередко подвергают геохимическому опробованию, чтобы изучить геохимические ореолы вокруг рудных тел и попутно выявить признаки не вскрытых разведочными выработками новых рудных тел. В разведочных выработках проводятся и другие исследования инженерно-геологического и гидрогеологического характера.
В процессе разведки создают банк координат устьев (начала) разведочных выработок, банк искривлений скважин или маркшейдерских замеров, чтобы определить положение разведочных выработок в недрах земной коры, банк геологической документации разведочных выработок и банк опробования (может быть несколько банков опробования – раздельно рядовые, групповые, минералогические, технические и технологические пробы). Все эти банки данных вначале создают на бумажных носителях, а потом переносят на машинные носители – в компьютер.
Таблица 6.1
Реестр разведочных скважин
| № п/п | Номер скважины | Координаты устья, м | Глубина скважины, м | ||
| Х | У | Z | |||
| 1911,2 | 863,0 | 290,6 | 613,0 | ||
| 1577,6 | 794,2 | 279,4 | 383,7 | ||
| 1752,3 | 713,4 | 282,8 | 421,4 |
Поскольку в большинстве случаев разведка месторождений осуществляется скважинами, приведем образцы банков данных именно по скважинам. Банки данных по горным выработкам принципиально от них не отличаются.
Банк координат устьев разведочных скважин (и поисковых скважин), который часто называется реестром скважин, рекомендуется оформлять в виде табл.6.1.
Полезно добавить в этот реестр год окончания бурения скважин, что позволяет в дальнейшем получать интересные данные по динамике разведки месторождения и другие полезные сведения.
6.2.2. Банк искривлений скважин
Банк искривлений скважин содержит данные о глубинах замеров искривлений, зенитных и азимутальных углах в пунктах замеров (табл.6.2).Этот банк данных позволяет определить положение ствола в пространстве. Замеры искривлений в скважинах проводят через 20-50 м. По опытным данным, среднее отклонение скважин от вертикали на глубине 1000 м составляет около 100 м, а на глубине 1500 м – около 200 м, хотя скважина первоначально задана вертикальной. Пока зенитный угол небольшой (до 1°) гироскопическим методом азимутальный угол измеряется весьма ненадежно. Чтобы точнее определять зенитный угол, часто задают начальный зенитный угол скважины порядка 3-5°.
|
Таблица 6.2 Замеры искривлений скважин
|
6.2.3. Банк геологической документации
Банк геологической документации включает номера скважин, интервалы документации и индексацию типов горных пород и руд (табл.6.3). Индексация позволяет сокращать и формализовать геологическую документацию и облегчает обработку данных.
Таблица 6.3
|
| Поделиться: |





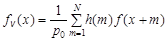 при
при  , (5.26)
, (5.26) при
при  . (5.27)
. (5.27) , (5.28)
, (5.28) . (5.29)
. (5.29) (5.30)
(5.30)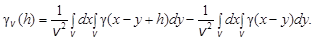 (5.31)
(5.31) , (5.32)
, (5.32)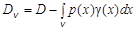 ; (5.33)
; (5.33)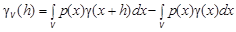 . (5.34)
. (5.34)
 Необходимо рассчитать прогнозное значение пространственной переменной в точке Z. Предположим, что геологический объект изотропный, тогда вокруг точки Z можно провести окружность с радиусом влияния R. Все измерения внутри окружности влияют на значение пространственной переменной в точке Z. За пределами окружности результаты измерений в прогнозировании не участвуют.
Необходимо рассчитать прогнозное значение пространственной переменной в точке Z. Предположим, что геологический объект изотропный, тогда вокруг точки Z можно провести окружность с радиусом влияния R. Все измерения внутри окружности влияют на значение пространственной переменной в точке Z. За пределами окружности результаты измерений в прогнозировании не участвуют. . (5.35)
. (5.35) , (5.36)
, (5.36) (5.37)
(5.37)


