Проекции отрезков суммируют с координатами устья скважин, получают координаты конца отрезка, т.е. координаты пункта искривления.
Подобные операции повторяют для каждого отрезка, в результате определяют координаты всех пунктов измерений искривлений последовательно, начиная с устья скважин:
Хi + 1 = Xi + dx; Уi + 1 = Уi + dу; Zi + 1 = Zi – dz. (6.3)
Обращает на себя внимание, что приращение dz берется со знаком минус, так как отсчет координаты Z ведется снизу вверх от уровня Мирового океана (в России от Крондштадского футштока). В некоторых странах (например, в Канаде) отсчет координаты Z осуществляется в обратном порядке – сверху вниз (например, в пакете Micromine). Некоторая сложность в расчетах возникает, если азимуты на концах отрезка переходят через 360°, что можно учесть введением отрицательного азимута, если он меньше 360°. Если замеры искривлений не доведены до забоя скважины, то оставшаяся часть скважины принимается прямолинейной с последними измеренными зенитным и азимутальным углами.
|
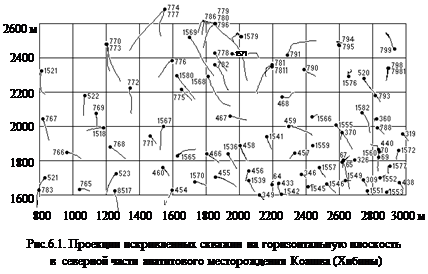
В результате расчетов получается банк координат искривленных скважин (табл.6.5), который позволяет показать положение скважин в пространстве на горизонтальной и на любой другой проекции (рис.6.1).
6.3.2. Банк рудных пересечений
В банке опробования содержатся рядовые пробы (см. табл.6.4), взятые по отдельным типам руд. Непрерывная совокупность рядовых проб дает рудное пересечение.
Рудное пересечение – это отрезок от точки входа до точки выхода из рудного тела.
Иногда внутри рудного пересечения располагаются руды различных промышленных сортов: окисленные и первичные, медные и цинковые, гематитовые и магнетитовые и пр. Тогда внутри рудного пересечения выделяются отдельные пересечения сортов руд. В каждом рудном пересечении или в пересечении промышленного сорта руды рассчитывают средний состав по формуле
 или
или  , (6.4)
, (6.4)
где m – длина проб; С – состав проб; r – плотность руды.
Когда плотность руды зависит от ее состава, применяется первая формула (6.4), в других случаях – вторая.
Таблица 6.6
Банк рудных пересечений
| № п/п | Номер скважины | Интервал, м | Сорт | Содержание, % | |||||
| От | До | Длина | Cu | Zn | S | ||||
| 38,4 | 40,2 | 1,8 | Ц | 0,22 | 6,43 | 32,15 | |||
| 40,2 | 43,6 | 3,4 | МЦ | 1,87 | 4,35 | 33,48 | |||
| 43,6 | 45,8 | 2,2 | М | 1,96 | 0,87 | 32,16 | |||
| 45.8 | 48,4 | 3,6 | МВ | 1,25 | 0,23 | 18,14 | |||
| Рудное пересечение | 38,4 | 48,4 | 10,0 | Р | 1,56 | 2,91 | 30,78 | ||
В результате подобных расчетов создается банк рудных пересечений (табл.6.6).Фактически в табл.6.6 два банка: банк сортов руд, а последняя строчка – составная часть банка рудных пересечений. Одна скважина может пересечь несколько рудных пересечений, так же, как и несколько однотипных горных пород.
6.3.3. Банк координат геологических границ
Имея банк данных геологической документации (см. табл.6.3), банк рудных пересечений (см. табл.6.6) и банк координат пунктов искривлений скважин (см. табл.6.5), можно рассчитать координаты всех геологических границ в скважинах. Координаты любой геологической границы в скважине находят путем линейной интерполяции между координатами соседних пунктов искривлений.
Пусть имеются координаты скважины на глубине 150 м (X 1 = 1254,2 м, Y 1 = 754,6 м, Z 1 = 247,4 м) и на глубине 200 м (X 2 = 1256,4 м, Y 2 = 752,8 м, Z 2 = 198,6 м). Требуется определить координаты геологической границы на глубине 183 м.
Ответ получаем по формуле линейной интерполяции (путем решения пропорции):
X = 1254,2 + (1256,4 – 1254,2)(183 – 150)/(200 – 150) = 1255,4 м;
Y = 754,6 + (754,6 – 752,8)(183 – 150)/(200 – 150) = 753,4 м;
Z = 247,4 – (247,4 – 198,6)(183 – 150)/(200 – 150) = 215,8 м.
Таблица 6.7
Банк геологических границ
| № п/п | Номер скважины | Координаты, м | Индекс | ||
| Х | Y | Z | |||
| 2154,3 | 1457,8 | 236,9 | ПГ | ||
| 2156,2 | 1458,0 | 232,7 | ИЗ | ||
| 2163,5 | 1462,1 | 200,6 | АРГ | ||
| 2165,7 | 1463,5 | 197,6 | Р | ||
| 2168,8 | 1471,4 | 148,9 | ГР | ||
| 23а | 1547,8 | 2175,5 | 233,3 | ПГ | |
| 23а | 1547,2 | 2176,1 | 230,8 | ПОРФ | |
| 23а | 1545,7 | 2187,3 | 208,1 | ИЗ |
Нужно обратить внимание, что приращение координаты Z идет со знаком минус. Подобным образом находят координаты всех геологических границ. В результате получают банк всех геологических границ (табл.6.7).
Расчетом банка геологических границ завершаются практически все направления математического моделирования геологических объектов. Далее пути моделирования расходятся. В геоинформатике, где главная задача состоит в построении геологических карт, основное внимание уделяется построению контуров геологических границ, их векторизации, введению условных обозначений для площадных и точечных объектов, созданию слоев с различной информацией, к преобразованию масштабов карт, к совмещению на одном чертеже нескольких слоев информации и т.д.
В данной книге мы не будем касаться геоинформатики, так как она входит в специальных курс «Математическая картография» и достаточно подробно изложена в работах В.Я.Цветкова [17, 18].
Рассмотрим второе направление – аналитическое – использование банка геологических границ для построения геологических карт и разрезов как одной из основ подсчета запасов и геолого-экономической оценки месторождений.
В конце книги коснемся методики построения и работы с блочными моделями месторождений.
6.4. О моделировании месторождений
6.4.1. Аналитические модели месторождений
В понятие аналитические модели месторождений вкладывается несколько иной смысл, чем в монографии И.И.Шаталова и В.И.Щеглова [19], где математическое моделирование ведется для создания искусственных учебных моделей месторождений. Здесь ставится задача построения графических изображений реальных месторождений на основе координат разведочных выработок. Эта задача довольно сложная и не всегда поддается исчерпывающему решению.
Можно выделить несколько уровней сложности месторождений применительно к математическому моделированию.
1. Наиболее простые месторождения разведаны короткими вертикальными разведочными выработками, единичные рудные тела однозначно увязаны между собой, разрывные нарушения, крутые складки и размывы отсутствуют.
2. Более сложные месторождения характеризуются наличием нескольких рудных тел, увязка которых неоднозначная и возможна лишь в диалоговом режиме. Могут присутствовать разрывные и складчатые нарушения и размывы. Разведочные выработки прямолинейные.
3. Месторождения следующей группы сложности отличаются тем, что скважины искривлены, но увязка рудных тел однозначная. Проблема заключается в основном в том, что скважины не лежат в одной плоскости, разведочные выработки часто находятся далеко друг от друга и интерполяция границ носит неоднозначный характер.
4. Наиболее сложная ситуация возникает, когда в разведочных скважинах много рудных пересечений, увязка их неоднозначная, скважины искривлены, не находятся в одной плоскости (рис.6.1) и трудно построить плоские разрезы. В данном случае кроме диалогового режима приходится принимать специальные меры по построению плоских разрезов.
Для месторождений последних двух групп рекомендуется сделать дополнительную опорную сеть вертикальных псевдоскважин, ориентированных по заданным профилям. Так, для скважин, изображенных на рис.6.1, построена опорная сеть псевдоскважин, расположенных по линиям с азимутом СЗ 235° в соответствии с генеральным направлением линий, принятых на месторождении (рис.6.2). Опорная сеть позволяет строить разрезы по линиям опорных скважин.
|
Идея заключается в том, чтобы, используя геологические границы в разведочных скважинах, подобные табл.6.7, путем интерполяции рассчитать координаты геологических границ во всех псевдоскважинах. Далее по координатам геологических границ, имеющихся в псевдоскважинах, проводят геологические границы в плоскостях вертикальных геологических разрезов. Создание сети псевдоскважин удобно во многих случаях математического моделирования месторождений.
Интерполяция координат геологических границ между разведочными скважинами может быть осуществлена различными способами. Наиболее приемлемый способ основан на комбинации тренда и кригинга. Вначале рассчитывается двухмерный тренд, потом остаток от тренда, по остаткам находится вариограмма и применяется кригинг по остаткам. Полезно отметить, что тренд частично снимает явление анизотропии. Наиболее сложная задача состоит в том, что перед расчетом тренда нужно идентифицировать рудные тела в диалоговом режиме. Иногда приходится рассчитывать несколько вариантов трендов, добиваясь наименьших отклонений поверхности тренда от координат рудных тел в разведочных скважинах.
Когда рудные тела индентифицированы, рассчитаны тренд, вариограмма остатков и определен радиус автокорреляции, можно прогнозировать значения координат геологических границ в опорных псевдоскважинах. При этом возникает несколько вариантов.
Если в пределы радиуса автокорреляции попадает более трех разведочных скважин, то кригинг осуществляется обычным способом по формуле (5.37). Если в пределах радиуса автокорреляции имеется одна или две разведочные скважины, то нужно найти вес координат геологической границы по формуле pi = D – g(h), где h – расстояние от опорной псевдоскважины до разведочной скважины, и далее воспользоваться формулой (5.37). Если псевдоскважина находится за пределами радиуса влияния разведочных выработок, то применяют либо линейную интерполяцию, либо интерполяцию методом обратных расстояний.
Еще одна проблема возникает при расщеплении или слиянии рудных тел или при выклинивании геологических тел. При слиянии рудных тел между ними проводится условная геологическая граница либо по геологическим данным, либо с помощью тренда. При графическом изображении эту границу, естественно, не показывают. При выклинивании геологических тел для каждой расщепленной части строится своя граница, которая совпадает с границей нижележащих пород или руд, т.е. мощность выклинившегося геологического тела считается нулевой.

|
Имея координаты геологических границ в каждой псевдоскважине, можно по ним построить вертикальный геологический разрез. Наилучший вариант получается, если в качестве геологической границы в разрезе используют сплайн (скользящий сплайн). Каждое геологическое тело имеет верхнюю и нижнюю границу. Их строят одновременно, но условные обозначения горной породы или руды (цветные или штриховые) задают верхней границей (рис.6.3).
6.4.2. Блочные модели месторождений
Как указывалось выше, месторождение с помощью сетки разбивается на элементарные одинаковые по размеру блоки. На маломощных рудных телах блоки имеют квадратную форму, а на мощных рудных телах – кубическую (рис.6.4 и 6.5).
|
Размер блоков может быть любой, но предпочтительнее делать блоки меньше эксплуатационных. На экране монитора размер блоков можно довести до пикселя. Обычно стараются выбрать блоки такого размера, чтобы в него попадало не менее трех разведочных выработок (в пределах радиуса автокорреляции). Чем больше в блоке разведочных выработок, тем достовернее будут определены в нем параметры.
Разбиению на блоки предшествует оконтуривание рудных тел («натягивание каркаса на рудное тело»). Блоки выделяют в пределах установленного каркаса. Используя различные методы интерполяции, описанные в главе 5, в каждом блоке по данным разведочных выработок определяют параметры оруденения (состав и плотность руды, запасы руд и металла, достоверность и категорийность запасов и др.).
Для построения блочных моделей месторождений разработано большое количество пакетов прикладных программ, такие как Datamine, Micromine, Minescape, Vulkan, Geostat и др.
Особенность пакетов состоит в специальной обработке банка опробования. Рудные пересечения делят на равные интервалы (например, по 3 м) без учета типов руд. В каждом интервале по данным рядовых проб без учета плотности руды рассчитывают среднее содержание металлов. Далее определяют координаты центров рудных интервалов (методику см. в подразделах 6.3.1 и 6.3.3), которые и используют в дальнейших расчетах. Попутно проверяют арифметические ошибки, которые могут появиться при ручном вводе исходных данных. Совокупность блоков дает пространственное представление о размещении оруденения. Для наглядности можно поворачивать полученное изображение в трехмерном пространстве. Блоки можно раскрашивать по содержанию металлов, по сортам руд, по достоверности запасов и т.д.
Суммируя содержимое блоков в заданных границах, можно рассчитать запасы руды, среднее содержание металлов как в отдельных блоках, так и по месторождению в целом.
Дополнительные программы, введенные в пакеты прикладных программ, позволяют проводить экономическую оценку месторождений (для этого потребуется дополнительная экономическая информация), обосновывать кондиции методом вариантов. Наконец, в пакетах имеются программы, предназначенные для проектирования рудников. Многообразие задач, решаемых с помощью моделей, обусловило их широкое применение при математическом моделировании и оценке месторождений.

Заключение
Рассмотренные математические методы не исчерпывают всего их многообразия. Приведены лишь наиболее важные и распространенные в геологической практике, по мнению автора, методы. Так, исключены из рассмотрения дисперсионный анализ, частные коэффициенты корреляции, некоторые редкие законы распределения случайных величин. Некоторые методы, например основы геостатистики, кригинг даны в сокращенном виде. Подробные сведения студенты могут найти в справочнике [15].
Вместе с тем в учебник включены новые методы, как созданные автором, так и заимствованные из других источников: нахождение информативных факторов, определение оптимального порядка полинома, обработка усеченного закона распределения, выделение отдельных синусоид из гармонического ряда и др. Данные методы проверены на практике и могут быть полезны при математической обработке геологических данных.
В геологии появились также такие новые математические методы, как фрактальный анализ, явления самоорганизации вещества и др. Они находятся в стадии становления, поэтому в учебник пока не вошли.
Нужно обратить внимание, что в работе мало говорится о применении компьютеров, хотя многие из рассмотренных методов содержатся в таких прикладных пакетах, как Статистика, Сёрфер, Excel и пр. В пакетах отсутствует прозрачность в идеологии вычислений, часто отсутствуют формулы, по которым производятся те или иные вычисления, дается лишь готовый результат. Прикладные пакеты удобны для подготовки презентаций, построения диаграмм различного типа, научных докладов, но по ним трудно изучать математические методы. Предполагается, что пользователь пакетов хорошо знаком с математическими методами и использует программы для иллюстративных целей.
Можно надеяться, что учебник будет полезен не только студентам, но и геологам-производственникам, а также другим специалистам, занимающимся математической обработкой данных. Математические методы большей частью универсальны и применимы в самых различных областях знаний.
рекомендательный библиографический список
1. Абрамович И.И. Математическая геология и математический прогноз / И.И.Абрамович, Л.Н.Дуденко, Ю.И.Михайлова // Тр. ВСЕГЕИ. 1972. Т.178. С.103-122.
2. Айвазян С.А. Прикладная статистика. Исследование зависимостей: Справочное пособие / С.А.Айвазян, И.Г.Енюков, Л.Д.Мешалкин. М.: Финансы и статистика, 1985. 187 с.
3. Афифи А. Статистический анализ. Подход с использованием ЭВМ / А.Афифи, С.М.Эйзен. М.: Мир, 1982. 488 с.
4. Большев Л.Н. Таблицы математической статистики / Л.Н.Большев, Н.В.Смирнов. М.: Наука, 1983. 416 с.
5. Боровиков В. Statistica. Искусство анализа данных на компьютере. 2-е изд. СПб: Питер, 2003. 688 с.
6. Бронштейн И.Н. Справочник по математике для инженеров и учащихся втузов / И.Н.Бронштейн, К.А.Семендяев. 13-е изд. М.: Наука, 1986. 544 с.
7. Давид М. Геостатистические методы при оценке запасов. Л.: Недра, 1980. 360 с.
8. Каждан А.Б. Математическое моделирование в геологии и разведке полезных ископаемых / А.Б.Каждан, О.И.Гуськов, А.А.Шиманский. М.: Недра, 1979. 168 с.
9. Каждан А.Б. Математические методы в геологии: Учебник для вузов / А.Б.Каждан, О.И.Гуськов. А.А.Шиманский. М.: Недра, 1990. 251 с.
10. Капутин Ю.Е. Геостатистическое исследование месторождений полезных ископаемых: Методические рекомендации. Петрозаводск: Изд-во КарФАН СССР, 1988. 190 с.
11. Математическая энциклопедия: В 5 томах. М.: Советская энциклопедия, 1977-1985.
12. Матерон Ж. Основы прикладной геостатистики. М.: Мир, 1968. 408 с.
13. Поротов Г.С. Основы статистической обработки материалов разведки месторождений: Учебное пособие / Ленинградский горный институт. Л., 1985. 97 с.
14. Смоляк С.А. Устойчивые методы оценивания / С.А.Смоляк, Б.П.Титаренко. М.: Статистика, 1980. 208 с.
15. Справочник по математическим методам в геологии / А.А.Родионов, Р.И.Коган, В.А.Голубев и др. М.: Недра, 1987. 334 с.
16. Тьюки Дж. Анализ результатов наблюдений. М.: Мир, 1981. 302 с.
17. Цветков В.Я. Геоинформационные системы и технологии. М.: Финансы и статистика, 1998. 288 с.
18. Цветков В.Я. Геоинформационные системы и технологии: Учебное пособие / Московский институт геодезии и картографии. М., 1996. 112 с.
19. Шаталов И.И. Моделирование месторождений и рудных полей на ЭВМ: Учебное пособие / И.И.Шаталов, В.И.Щеглов. М.: Недра, 1989. 150 с.
20. Шестаков Ю.Г. Математические методы в геологии: Учебное пособие. Красноярск: Изд-во Красноярского ун-та, 1988. 208 с.
Оглавление
Введение.................................................................................................................... 3
Глава 1. Общие сведения......................................................................................... 7
1.1. Геологические объекты и их свойства....................................................... 7
1.1.1. Понятие о геологических объектах.................................................. 7
1.1.2. Свойства геологических объектов................................................... 9
1.1.3. Выборочные методы изучения геологических объектов............... 11
1.2. Понятие о математическом моделировании геологических объектов... 13
1.2.1. Принцип и операции математического моделирования.................. 13
1.2.2. Примеры математических моделей.................................................. 16
1.2.3. Основные виды математических моделей, применяемых в геологии 20
Глава 2. Одномерная статистическая модель и ее применение в геологии......... 23
2.1. Одномерная статистическая модель.......................................................... 23
2.1.1. Свойства геологических объектов как независимые случайные величины 23
2.1.2. Статистические характеристики случайной величины.................... 24
2.1.3. Моменты случайной величины, их связь со статистическими характеристиками 28
2.1.4. Группировка исходных данных. Построение гистограммы........... 32
2.1.5. Расчет статистических характеристик по сгруппированным данным 34
2.2. Законы распределения случайных величин............................................... 37
2.2.1. Понятие о законах распределения.................................................... 37
2.2.2. Нормальный закон распределения................................................... 39
2.2.3. Логарифмически-нормальный закон распределения...................... 45
2.2.4. Распределение Стьюдента................................................................. 47
2.2.5. Распределение c2................................................................................ 52
2.2.6. Распределение Фишера...................................................................... 54
2.2.7. Построение графика плотности вероятности, проверка гипотезы о законе распределения 56
2.2.8. Преобразование случайной величины.............................................. 60
2.3. Геологические приложения одномерной статистической модели........... 64
2.3.1. Точечная оценка погрешности среднего значения.......................... 64
2.3.2. Интервальная оценка математического ожидания случайной величины 65
2.3.3. Выделение аномальных значений..................................................... 67
2.3.4. Выделение однородных совокупностей........................................... 75
Глава 3. Двухмерная статистическая модель и ее применение в геологии.......... 78
3.1. Двухмерная статистическая модель.......................................................... 78
3.1.1. Система двух случайных величин и ее графическое изображение 78
3.1.2. Статистические характеристики системы двух случайных величин. Коэффициент корреляции 80
3.1.3. Уравнение линейной регрессии......................................................... 84
3.1.4. Двухмерное нормальное распределение. Эллипс рассеяния.......... 87
3.1.5. Нелинейная регрессия. Метод наименьших квадратов.................. 90
3.1.6. Применение метода наименьших квадратов к параболической зависимости 92
3.1.7. Выбор порядка полинома при аппроксимации нелинейной зависимости 96
3.1.8. Приведение нелинейных зависимостей к линейному виду............. 97
3.2. Геологические приложения двухмерной статистической модели........... 98
3.2.1. Прогнозирование свойств по уравнению регрессии....................... 98
3.2.2. Выявление аномальных значений и однородных совокупностей.. 98
3.2.3. Внутренний контроль химических анализов................................... 99
3.2.4. Внешний контроль химических анализов........................................ 102
3.2.5. Оценка различия между геологическими объектами..................... 106
3.2.6. Оценка постоянной радиоактивного распада................................... 107
3.2.7. Зависимость плотности руды от ее состава..................................... 109
3.2.8. Вычисление параметров усеченного нормального распределения 111
Глава 4. Многомерная статистическая модель и ее применение в геологии....... 115
4.1. Многомерная статистическая модель....................................................... 115
4.1.1. Система множества случайных величин и ее статистические характеристики 115
4.1.2. Множественная линейная регрессия. Коэффициент множественной корреляции 117
4.1.3. Отбор информативных свойств в уравнении множественной линейной регрессии 121
4.2. Применение многомерной статистической модели в геологии............... 124
4.2.1. Анализ матрицы коэффициентов корреляции................................. 124
4.2.2. Метод главных компонент................................................................ 126
4.2.3. Кластерный анализ. Дендрограмма.................................................. 136
4.2.4. Распознавание образов...................................................................... 141
Глава 5. Математическое моделирование пространственных геологических закономерностей 159
5.1. Свойства геологических объектов как пространственные переменные.. 159
5.2. Виды математических моделей и геологических полей........................... 161
5.3. Детерминированные модели геологических полей.................................. 163
5.3.1. Линейная интерполяционная модель............................................... 163
5.3.2. Полиномиальная модель.................................................................. 166
5.3.3. Модель обратных расстояний........................................................... 167
5.3.4. Сплайн-модель................................................................................... 169
5.4. Вероятностные модели геологических полей........................................... 173
5.4.1. Модель на основе случайной функции............................................ 173
5.4.2. Гармонический анализ....................................................................... 183
5.4.3. Периодограммный анализ................................................................. 189
5.5. Основы геостатистики................................................................................ 191
5.5.1. Вариограмма и ее аппроксимации.................................................... 191
5.5.2. Влияние на вариограмму геометрической базы измерений........... 195
5.5.3. Понятие о кригинге........................................................................... 198
Глава 6. Основы математического моделирования месторождений.................... 203
6.1. Задачи математического моделирования месторождений....................... 203
6.2. Банки исходных данных при разведке месторождений............................ 205
6.2.1. Банк координат устьев разведочных выработок............................. 205
6.2.2. Банк искривлений скважин............................................................... 206
6.2.3. Банк геологической документации................................................... 207
6.2.4. Банк опробования.............................................................................. 208
6.3. Вторичные (расчетные) банки данных....................................................... 209
6.3.1. Банк координат пунктов измерения искривлений........................... 209
6.3.2. Банк рудных пересечений.................................................................. 211
6.3.3. Банк координат геологических границ............................................. 212
6.4. О моделировании месторождений....................................................... 213
6.4.1. Аналитические модели месторождений........................................... 213
6.4.2. Блочные модели месторождений...................................................... 216
Заключение............................................................................................................... 219
Рекомендательный библиографический список..................................................... 220
* Компонента – новая координата точки в признаковом пространстве после переноса и вращения системы координат.
|
| Поделиться: |