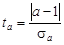 при
при 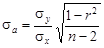
и 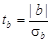 при
при 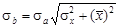 .
.
Если хотя бы один из критериев больше допустимого t доп, то систематическая погрешность установлена. Значения t доп берут из табл.2.10 при вероятности b = 0,05 и числе степеней свободы k = n – 2.
Если систематическая погрешность установлена, то в основные данные могут быть введены поправки по уравнению регрессии y = ax + b. Подставляя в него содержания в основных пробах xi, можно получить исправленные значения yi, не содержащие систематической погрешности. В особо ответственных случаях контроль проводят несколько раз, чтобы убедиться в обоснованности введения поправок на систематическую погрешность.
8 Пример 3.4. В 24 пробах выполнены основные и контрольные анализы на серу (табл.3.6, рис.3.10). Требуется определить, имеется ли систематическая погрешность в основных анализах.
В результате статистической обработки рассчитаны характеристики:  = 1,934;
= 1,934;  = 1,775; s х = 1,185; s у = 1,100; r = 0,997. Из них получено уравнение регрессии у = 0,9253 х – 0,0181. На рис.3.10 видно, что линия регрессии несколько смещена относительно биссектрисы, что свидетельствует о возможной систематической погрешности.
= 1,775; s х = 1,185; s у = 1,100; r = 0,997. Из них получено уравнение регрессии у = 0,9253 х – 0,0181. На рис.3.10 видно, что линия регрессии несколько смещена относительно биссектрисы, что свидетельствует о возможной систематической погрешности.
Вычислим необходимые величины:
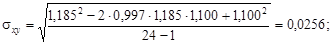
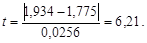
Из табл.2.10 при вероятности b = 0,05 и числе степеней свободы k = 24 – 1 = 23 найдем допустимую величину критерия t доп = 2,069. Так как t > t доп, то систематическая погрешность доказана.
Проверим наличие систематической погрешности по величине коэффициентов регрессии:
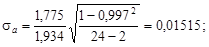
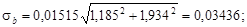
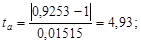
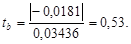
Из табл.2.10 при вероятности b = 0,05 и числе степеней свободы k = 24 – 2 = 22 допустимое значение критерия t доп = 2,074. Так как ta > t доп, то систематическая погрешность доказана.
Поправка на систематическую погрешность, выполненная по уравнению регрессии, дает исправленные значения содержания в основных пробах (табл.3.6).7
|
|
3.2.5. Оценка различия между геологическими объектами
Оценку сходства или различия между геологическими объектами можно производить по характеристикам как каждого отдельного свойства, так и множества свойств. Ограничимся оценкой различия по одному свойству.
Пусть имеются два геологических объекта, в каждом из которых имеется несколько измерений характеристик одного свойства. Средние значения  и
и  , дисперсии
, дисперсии 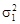 и
и 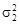 , число измерений n 1 и n 2. Решение о различии объектов принимается с помощью критерия t с использованием распределения Стьюдента при вероятности b = 0,05 и числе степеней свободы k = n 1 + n 2 – 2:
, число измерений n 1 и n 2. Решение о различии объектов принимается с помощью критерия t с использованием распределения Стьюдента при вероятности b = 0,05 и числе степеней свободы k = n 1 + n 2 – 2:
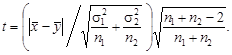 (3.35)
(3.35)
Если критерий t будет больше допустимого t доп при заданной вероятности (см. табл.2.10), то имеются существенные различия между геологическими объектами.
При увеличении числа наблюдений распределение Стьюдента стремится к нормальному и критерий t стремится к пределу, выражаемому формулой
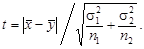 (3.36)
(3.36)
Эта формула обычно и применяется на практике.
8 Пример 3.5. Проанализированы две серии проб базальтов из различных потоков вулкана. Средние содержания кремнезема составляют соответственно 50,35 и 49,76 %, дисперсии содержаний 4,16 и 3,32, число проб 20 и 25. Нужно установить, различаются ли базальты по содержанию кремнезема.
Число степеней свободы k = 20 + 25 – 2 = 43. Вычислим критерий Стьюдента:
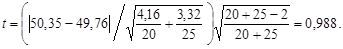
Из табл.2.10 при вероятности b = 0,05 и числе степеней свободы 43 найдем допустимое значение критерия t доп = 2,01. Так как t < t доп, то базальты по содержанию кремнезема не различаются.7
Различия между совокупностями измерений можно оценивать не только по средним значениям, но и по другим статистическим характеристикам: по дисперсиям, асимметриям и эксцессам. Сравнение дисперсий основано на F -распределении (см. подраздел 2.2.6). Сравнение асимметрий и эксцессов проводится по критериям Стьюдента или нормального закона:
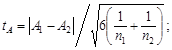
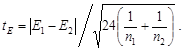 (3.37)
(3.37)
3.2.6. Оценка постоянной радиоактивного распада
Как известно, радиоактивный распад атомов происходит по экспоненциальному закону:
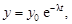 (3.38)
(3.38)
где у 0 – число распадов в произвольный начальный момент времени t = 0; l – постоянная распада.
|
|
Если имеются измерения радиоактивности у в различные моменты времени t,то можно рассчитать постоянную l, которая связана с периодом полураспада T соотношением T = ln2/l. Период полураспада – это время, в течение которого распадается половина атомов. Эта величина является постоянной для каждого изотопа и позволяет идентифицировать его.
|
Таблица 3.7
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.140.96 (0.009 с.) |






