
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормированный состав магнетитаСодержание книги
Поиск на нашем сайте
Их вычисляют для каждого фактора и пробы отдельно. Например, для первого фактора имеем
Совокупность значений z для всех проб магнетита, рассчитанная по формуле (4.11), приведена в табл.4.14. Дисперсия значений z по каждому фактору равна собственному числу λ, что служит еще одной проверкой правильности всех предыдущих вычислений. Таблица 4.14 Главные компоненты z
Таблица 4.15 Средний состав групп магнетита, %
Главные компоненты (табл.4.14) позволяют изобразить проекцию облака точек на любую плоскость в новых координатах. Обычно используется проекция точек на первые две оси (рис.4.2), но можно выбрать и другие пары координатных осей. Подобные графики также несут геологическую информацию. Расположение точек на проекции позволяет выявить однородные совокупности или отдельные аномальные значения, т.е. может быть использовано для классификации объектов. На рис.4.2 видно, что магнетиты различаются по составу, соответствующие точки группируются в два облака. Кроме того, две точки удалены от облаков, что свидетельствует об аномальности двух проб магнетита. Следовательно, имеются две однородные группы магнетита и две аномальные пробы магнетита (группы состоят из отдельных проб). Чтобы определить, какие точки соответствуют различным номерам проб, следует обратиться к табл.4.14 (первые два фактора), где приведены координаты точек в новой системе координат. Аномальными являются пробы 8 и 14. Малое облако точек соответствует пробам 6, 17 и 18. В большом облаке находятся точки остальных проб. Имеет смысл рассчитать средний состав групп и сравнить их между собой (табл.4.15).7
Иногда на рисунках главных компонент имеется только одна однородная совокупность. В некоторых случаях вместо облаков точек наблюдаются ряды точек, отражающие особенности эволюции свойств объектов в пространстве или во времени (рис.4.3). На рисунки часто выносят значения главных факторных нагрузок, которые позволяют наглядно видеть направленность свойств в признаковом пространстве.
На рис.4.3 отчетливо видны два эволюционных ряда. В одном ряду преобладают акцессорные хромиты, в другом – рудные хромиты. Вероятно, они различаются способом образования. Чтобы определить состав хромитов двух ветвей, нужно рассчитать состав хромита в каждой ветви. Эта процедура выполняется с помощью значений главных компонент, таких же, как в табл.4.14. Выполненные расчеты по образцу табл.4.15 показали, что верхний эволюционный ряд, где расположены преимущественно акцессорные магнетиты, направлен в сторону алюмохромитов, а нижний эволюционный ряд – в сторону магнохромитов.
Итак, метод главных компонент позволяет выделить однородные совокупности и аномальные значения, а также дать геологическую интерпретацию причин изменения свойств объектов по значениям факторных нагрузок.
4.2.3. Кластерный анализ. Дендрограмма
На основе многомерной статистической модели разработан еще один способ классификации объектов по множеству свойств – кластерный анализ. Существо его заключается в выделении однородных групп объектов и в установлении количественной меры сходства (различия) между объектами и группами объектов. Пусть имеется совокупность геологических объектов, обладающих множеством свойств. Сведения о свойствах образуют матрицу (4.1). Геометрическая аналогия матрицы – облако точек в многомерном признаковом пространстве, в котором отдельные точки соответствуют единичным объектам. При кластерном анализе исследуется взаимное расположение точек. Чем ближе расположены точки, тем более сходны между собой соответствующие объекты. Задача состоит в том, чтобы объединить скопления близлежащих точек, соответствующие однородным группам объектов. Эти группы называются кластерами, что и дало название методу. Поставленная задача имеет много вариантов решения. Вначале необходимо выбрать масштаб по осям координат. Если величины имеют одинаковую размерность и приблизительно один порядок, то применяют натуральный масштаб – по координатным осям откладывают исходные свойства. Если величины различаются размерностью или порядком значений, то необходима нормализация свойств. Один из способов нормализации основан на использовании размаха значений х max – х min и осуществляется по формуле
где х – исходные; t – преобразованные (нормализованные) свойства, нормализованные значения меняются от нуля до +1. Второй способ нормализации производится по формуле
Здесь нормализованные значения колеблются от –1 до +1. Третий способ нормализации выполняется по формуле (2.24), в которой в качестве масштаба используется среднеквадратичное отклонение σ. При нормальном распределении свойства нормализованные значения заключены в основном в пределах от –3 до +3, при иных законах могут выходить за эти пределы. Когда масштаб по координатным осям задан, можно приступить к определению мер сходства (различия) между объектами по множеству свойств. Наиболее распространенная мера сходства между объектом i и объектом j – это взвешенное евклидово расстояние между точками в многомерном признаковом пространстве:
Напомним, что k – число свойств. Чем меньше ρ ij, тем ближе расположены точки в признаковом пространстве, тем больше сходство между соответствующими объектами. В качестве меры сходства можно применять среднеарифметическое значение абсолютных значений свойств:
Иной характер имеет угловая мера сходства, основанная на корреляционной связи между объектами:
Она характеризует косинус угла между двумя многомерными векторами, соединяющими начало координат с точкой i и с точкой j. Эта мера заключена в пределах от –1 до +1. Чем она ближе к +1, тем больше сходство между объектами. Чем она ближе к –1, тем больше различие между объектами. Применение данной меры оправданно, если точки находятся приблизительно на одном удалении от начала координат, так как расстояние между точками не учитывается.
Существует много других мер сходства (различия) между объектами, их обзор дан в справочнике [15]. Если имеется совокупность из n объектов, то совокупность мер сходства между всеми парами объектов составляет симметричную матрицу размером n ´ n. Если используется формула (4.14) или (4.15), то матрица сходства имеет вид По диагонали матрицы расположены нули, которые можно заменить прочерками. Чем меньше мера сходства, тем больше объекты сходны между собой. Если используется мера сходства (4.16), то матрица сходства имеет другой вид:
В этой матрице, чем ближе мера сходства к +1, тем объекты более сходны между собой. В ходе кластерного анализа близкие между собой объекты объединяются в группы (кластеры). Вначале находят два объекта, наиболее близких между собой. Их свойства усредняют, и далее они выступают как один объект (кластер). Находят меры сходства полученного кластера со всеми остальными объектами. Данная операция объединения объектов продолжается, пока все они не объединятся в один объект. В итоге получается последовательность объединения объектов и мера сходства на каждом шаге объединения. Эти данные изображают на графике, который называется дендрограммой. По оси абсцисс откладывают номера объектов в порядке объединения, а по оси ординат – соответствующие меры сходства.
8 Пример 4.5. Имеется 14 анализов циркона на пять компонентов (табл.4.16). Необходимо провести кластерный анализ.
Таблица 4.16 Состав циркона, %
Предварительно все свойства нормализуем по формуле (2.14). После вычисления матрицы сходства (4.17) стало ясно, что наименьшая мера сходства 0,302 имеется между пробами 5 и 12. Объединим их в кластер и усредним. Далее они выступают как одна проба. Следующая наиболее близкая пара объектов с мерой сходства 0,451 – это объекты 6 и 14. Продолжая объединение проб и кластеров далее, получим следующую последовательность объединения проб:
В последней строке все пробы объединились в один кластер. На дендрограмме, построенной по этим данным (рис.4.4), видна последовательность объединения проб. Кроме того, на графике выделяются, по крайней мере, четыре группы проб (четыре типа цирконов по составу) и три пробы (13, 3 и 7), отличающиеся от других проб по составу.7
Таким образом, кластерный анализ позволяет выполнить группировку объектов по степени их сходства по множеству свойств. Группировка при кластерном анализе может несколько отличаться от группировки по методу главных компонент, так как в основу этих методов заложены различные критерии. Можно сказать, что кластерный анализ дополняет метод главных компонент и помогает принять более правильное решение при выделении однородных совокупностей. Кроме того, представляет интерес и сама дендрограмма, наглядно характеризующая типизацию объектов по их свойствам.
4.2.4. Распознавание образов
Постановка задачи о распознавании образов. В геологической практике часто необходимо определить принадлежность объекта по множеству свойств к заданной совокупности однородных объектов. Сюда относятся задачи выделения перспективных территорий, оценки рудопроявлений, отнесения руд к какому-либо типу и многие другие. Решение подобных задач основано на приемах распознавания образов. Образ – это совокупность однородных эталонных объектов с набором свойств. Образ выражается матрицей свойств (4.1), в признаковом пространстве ему соответствует облако точек. В задачах распознавания обычно участвует не менее двух образов, а также испытуемые объекты. Задача распознавания заключается в определении принадлежности каждого испытуемого объекта к тому или иному образу. Распознавание образов наиболее часто используется при поисках месторождений, хотя область его применения гораздо шире.
Пусть имеется n перспективных территорий с заведомо промышленным оруденением определенного типа. Совокупность таких территорий, обладающих множеством свойств, создает образ рудных объектов. Им соответствует матрица свойств
Далее имеется m заведомо неперспективных территорий, где оруденение отсутствует, – это образ безрудных объектов:
Наконец, имеются группы из l испытуемых территорий, перспективность которых неизвестна, им соответствует матрица
У всех объектов должны быть измерены одни и те же величины (например, длина, мощность и т.д.). Цель исследования состоит в определении, к какому образу – рудному или безрудному – относится каждая из испытуемых территорий. Может быть задано несколько типов рудных объектов и, соответственно, рудных образов. Испытуемые объекты могут быть объединены с безрудными. Иногда рудные объекты делят на две части. Одна часть используется «для обучения», другая – «для экзамена», т.е. для проверки эффективности методики распознавания. Существует много способов решения задачи распознавания. Последовательность операций по решению задачи распознавания называется решающим правилом или алгоритмом распознавания. Определение информативных свойств. Распознаванию образов предшествует отбор информативных свойств, чтобы исключить из рассмотрения неинформативные свойства и сократить объем вычислений. Более того, избыток неинформативных свойств ухудшает результаты распознавания образов. Один из методов определения информативности свойств основан на оценке частот сочетаний качественных свойств рудных объектов, поскольку сочетания свойств более информативны, чем сумма информативностей отдельных свойств. Например, оруденение может появляться при благоприятном сочетании нескольких свойств (при пересечении разрывных нарушений, на контакте интрузивных пород с определенными литологическими типами горных пород и т.д.). В простейшем случае информативность J отдельного свойства i определяется по формуле
где n – число объектов; k – число свойств; Nij – частота совместного появления свойства i и свойства j. Расположив свойства в порядке информативности, можно найти суммарную информативность m свойств:
Известны приложения рассмотренного приема к определению информативности руководящей фауны. В алгоритме распознавания образов «Кора-3», предложенного М.М.Бонгардом [15], используются не только двойные, но тройные сочетания свойств. 8 Пример 4.6. Имеется шесть рудных объектов, у которых измерено пять качественных свойств:
Требуется определить информативность свойств. По формуле (4.22) найдем информативность первого свойства:
Здесь числа в скобках – частота сочетания первого свойства со всеми свойствами (включая первое) в квадрате. Аналогично найдем информативность остальных свойств. В результате получим набор (вектор) информативности всех свойств: { J } = (0,32 0,57 0,28 0,39 0,53). Наиболее информативным оказалось второе свойство, далее идут пятое, четвертое, первое и третье свойства. По формуле (4.23) определим суммарную информативность, последовательно добавляя свойства в порядке убывания их информативности: { Jm } = (0,57 0,78 0,87 0,93 0,97). Если принять информативность суммы всех свойств за 100 %, то на долю двух важнейших свойств приходится 81 %, а при добавлении третьего свойства она возрастет до 90 %. Для решения задачи распознавания образов можно ограничиться тремя первыми свойствами.7
Второй метод определения информативности качественных свойств основан на энтропии свойства j:
где р 1 i и p 2 i – частота появления свойства j соответственно на рудных и безрудных объектах.
Чем больше частоты р 1 i и p 2 i отличаются друг от друга, тем более информативны соответствующие свойства. Пример применения формулы (4.24) приведен в работе [1], где оценена информативность свойств в районе развития медно-никелевых месторождений и выделены территории, наиболее перспективные на поиски этого оруденения (рис.4.5). Информативность количественных свойств оценивают путем анализа расстояний между облаками точек рудных и безрудных объектов в признаковом пространстве. Информативность свойства j характеризуется квадратом нормированного расстояния между проекциями центров облаков на ось j признакового пространства:
где Дисперсию определяют по формуле
где n 1 и n 2 – количество соответственно рудных и безрудных объектов; Чем больше значение Jj, тем более информативным является данное свойство. Учет зависимости между свойствами может изменить порядок информативности свойств. На основе матриц исходных данных составляют матрицы ковариации для рудных
Далее определяют средневзвешенную матрицу ковариации по формуле, аналогичной (4.26). Элементы средневзвешенной матрицы
Из элементов матрицы составляют систему из k уравнений с неизвестными коэффициентами a 1, a 2, …, аk, которые находят путем решения этой системы:
где Kij – средневзвешенные корреляционные моменты между свойствами объектов (раздельно для рудных и безрудных объектов). Информативность k количественных свойств выражается квадратом обобщенного расстояния между облаками в признаковом пространстве:
Отсюда вытекает порядок определения информативности свойств. Вначале по формуле (4.25) отыскивают наиболее информативное свойство. К нему поочередно добавляют каждое из оставшихся свойств, находя наиболее информативную комбинацию из двух свойств по формуле (4.27). Далее добавляют следующее свойство и снова находят наиболее информативное сочетание свойств. Повторяя эти операции, определяют все последующие свойства в ряду информативности. Отбор информативных свойств прекращается, когда дальнейшее их увеличение не приводит к заметному повышению совместной информативности.
8 Пример 4.7. Имеется 10 рудных и 14 безрудных объектов, у которых изучено пять свойств:
{ x } = Требуется определить информативность свойств. Найдем средние значения свойств:
Далее вычислим дисперсии значений свойств:
По формуле (4.26) рассчитаем дисперсии разности средних значений свойств:
По формуле (4.25) найдем квадраты расстояний:
Из полученных данных видно, что наибольшей информативностью обладает второе свойство, далее идут третье, четвертое, пятое и первое. Рассмотрим, как изменится информативность свойств, если учитывать зависимости между ними. Вначале рассчитаем матрицы ковариации свойств рудных и безрудных объектов по формуле (4.27):
Далее найдем средневзвешенную матрицу по формуле (4.28):
Как отмечалось, наиболее информативным является второе свойство, для него r2 = 5,52. Будем поочередно добавлять ко второму свойству остальные и вычислять совместную информативность двух свойств. Так, найдем совместную информативность первого и второго свойств. Матрица их ковариации, согласно (4.28), имеет вид
Составим систему уравнений (4.29):
Решая систему, найдем Так же оценивается совместная информативность второго свойства с третьим, четвертым и пятым свойствами. Имеем
откуда видно, что для распознавания образа достаточно ограничиться двумя свойствами (вторым и третьим), остальные свойства вносят малый вклад в информативность и могут быть отброшены.7
Методы распознавания образов. После отбора информативных свойств можно приступать к распознаванию образов. Методы распознавания образов весьма многочисленны. Их можно разделить на три группы: · методы, основанные на анализе частоты появления свойств; · методы, основанные на анализе расстояний между точками объектов в многомерном признаковом пространстве; · методы, основанные на разделении многомерного признакового пространства на области различной формы, в каждой из которых преобладают объекты одного вида. В настоящей работе не ставится задача дать обзор различных методов распознавания образов [15], ограничимся лишь примерами алгоритмов в каждой из групп. Следует отметить, что не существует методов, дающих стопроцентный результат распознавания. Хорошим результатом считается уверенное распознавание испытуемых объектов на уровне 75-85 %. При частотном анализе исходные свойства выражаются нулями и единицами, т.е. одни свойства у объекта есть, другие отсутствуют. В алгоритме «Кора-3» перебираются все двойные и тройные комбинации свойств, которые характерны для одного образа и отсутствуют у другого. Найденные комбинации свойств называются сложными признаками. Для каждого испытуемого объекта определяется количество сложных признаков каждого образа. Испытуемый объект относят к образу рудных или безрудных объектов по большинству «голосов».
8 Пример 4.8. Имеются шесть рудных, шесть безрудных и три испытуемых объекта, у которых изучены четыре свойства:
Требуется выявить сложные признаки и определить принадлежность каждого испытуемого объекта к образу рудных или безрудных объектов. Нетрудно установить, что существует 11 сочетаний свойств по два и по три, которые имеются у рудных объектов и отсутствуют у безрудных, и, наоборот, 13 сочетаний свойств типичны только для безрудных объектов. Всего имеем 11 + 13 = 24 сложных признака (табл. 4.17). Таблица 4.17 Сложные признаки
Используя сведения по испытуемым объектам и данные табл.4.17, можно подсчитать, что для первого испытуемого объекта характерны признаки только рудных объектов, для второго – только безрудных, у третьего испытуемого объекта есть те и другие признаки, но больше «голосов» в пользу безрудных объектов (табл.4.18).7
Другой алгоритм распознавания основан на анализе образов рудных и безрудных объектов, которые в признаковом пространстве слагают два соответствующих облака, которые могут частично перекрывать друг друга. Принадлежность испытуемого объекта к образу рудных или безрудных объектов можно оценить по расстоянию точки испытуемого объекта от облаков. К какому облаку ближе точка, к тому образу и следует отнести испытуемый объект. Существуют различные способы оценки расстояний между точкой и облаком. Можно рекомендовать следующий способ: вначале найти расстояния до всех точек облака, а потом взять среднее из них. Для оценки расстояния между точкой испытуемого объекта х исп и точкой облака хi применима формула
где x maxи x min – максимальные и минимальные значения различных свойств i; x max– x min – размах свойств. Далее вычислим среднее расстояние точки до облака:
8 Пример 4.9. Даны пять рудных, шесть безрудных и два испытуемых объекта, у которых изучены три свойства:
Требуется определить принадлежность испытуемых объектов к рудным или к безрудным. Вначале найдем максимальные и минимальные значения свойств:
По формуле (4.31) определим расстояние точки первого испытуемого объекта от одной из точек облака рудных объектов:
Таким же способом найдем расстояние для всех остальных точек облаков и рассчитаем среднее расстояние до каждо
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.114 (0.017 с.) |


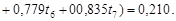
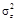


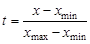 , (4.12)
, (4.12)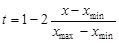 . (4.13)
. (4.13) . (4.14)
. (4.14)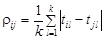 . (4.15)
. (4.15)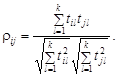 (4.16)
(4.16)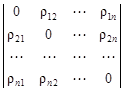 . (4.17)
. (4.17)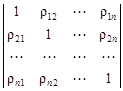 . (4.18)
. (4.18)
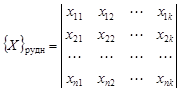 . (4.19)
. (4.19)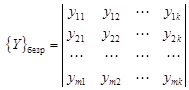 . (4.20)
. (4.20)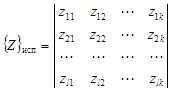 . (4.21)
. (4.21) , (4.22)
, (4.22)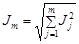 . (4.23)
. (4.23)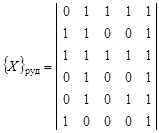 .
.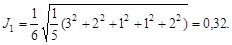
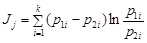 , (4.24)
, (4.24)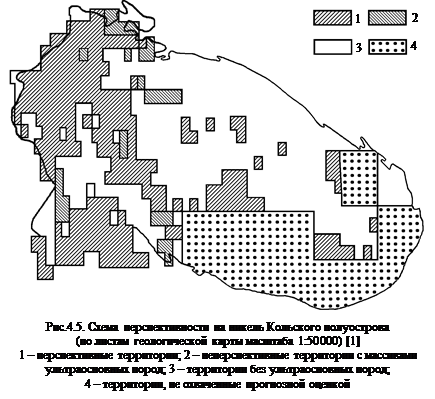
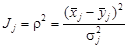 , (4.25)
, (4.25) и
и  – средние значения свойства j рудных и безрудных объектов.
– средние значения свойства j рудных и безрудных объектов. , (4.26)
, (4.26) и
и  – дисперсии свойства j тех же объектов.
– дисперсии свойства j тех же объектов. и безрудных
и безрудных  объектов. Элементы матриц находят из выражения
объектов. Элементы матриц находят из выражения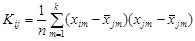 . (4.27)
. (4.27) . (4.28)
. (4.28)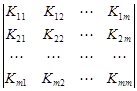
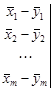 , (4.29)
, (4.29) . (4.30)
. (4.30) ;
;  .
.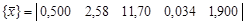 ;
; .
.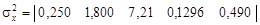 ;
;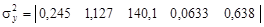 .
. .
.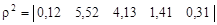 .
.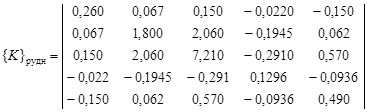 ;
; .
.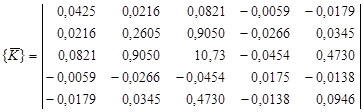 .
.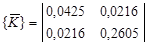 .
.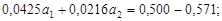
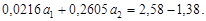
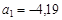 ;
;  Совместная информативность первого и второго свойств по формуле (4.30)
Совместная информативность первого и второго свойств по формуле (4.30)  , что больше, чем их сумма
, что больше, чем их сумма 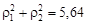 , т.е. информативность двух свойств с учетом зависимости больше, чем без ее учета.
, т.е. информативность двух свойств с учетом зависимости больше, чем без ее учета. ;
; 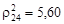 ;
; 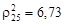 ; следовательно, наиболее информативным является сочетание второго и третьего свойств. К этим двум свойствам поочередно добавляют оставшиеся свойства (первое, четвертое и пятое) и по той же методике находят наиболее информативную комбинацию трех, четырех и пяти свойств. В рассматриваемом примере порядок наиболее информативных свойств следующий: второе, третье, первое, пятое и четвертое, т.е. иной, чем без учета зависимости между свойствами. Совместная информативность перечисленных свойств в нарастающем порядке выражается строкой матрицы
; следовательно, наиболее информативным является сочетание второго и третьего свойств. К этим двум свойствам поочередно добавляют оставшиеся свойства (первое, четвертое и пятое) и по той же методике находят наиболее информативную комбинацию трех, четырех и пяти свойств. В рассматриваемом примере порядок наиболее информативных свойств следующий: второе, третье, первое, пятое и четвертое, т.е. иной, чем без учета зависимости между свойствами. Совместная информативность перечисленных свойств в нарастающем порядке выражается строкой матрицы ,
, ;
;  ;
;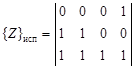 .
.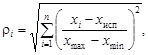 (4.31)
(4.31)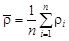 . (4.32)
. (4.32)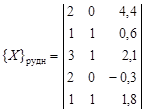 ;
; 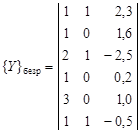 ;
; 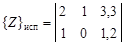 .
.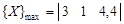 ;
;  .
.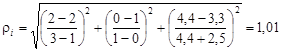 .
.


