
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы распределения случайных величинСодержание книги
Поиск на нашем сайте
2.2.1. Понятие о законах распределения При увеличении числа наблюдений частости стремятся к пределу, который характеризует вероятность появления случайной величины, а гистограмма частостей стремится к кривой, отражающей закон распределения вероятностей. Вид кривой определяется сущностью изучаемого свойства. Иногда на вид кривой влияет методика измерений, например выбор размера проб. Число видов кривых и, соответственно, законов распределения бесконечно велико, но некоторые из них имеют теоретическое обоснование и встречаются чаще других. По крайней мере, реальные распределения приближаются к этим законам. Закон распределения случайной величины наиболее часто выражается в виде интеграла вероятности:
где F (х) – вероятность p того, что значение случайной величины не превысит значения х, т.е. p = F (х); функция под интегралом f (x) – плотность вероятности случайной величины; к кривой, описываемой функцией f (x), стремится гистограмма частостей при увеличении числа наблюдений. Интеграл вероятности F (х) при увеличении значения х монотонно растет от нуля до единицы (рис.2.2). Интеграл вероятности (2.20) можно рассматривать как площадь (заштрихована на рис.2.2, б), ограниченную осью абсцисс, кривой f (x) и отрезком перпендикуляра, проведенного из точки а. Вся площадь под кривой f (x) равна единице, поэтому заштрихованная площадь меньше единицы и соответствует вероятности p.
Законы распределения случайных величин бывают дискретные и непрерывные. У дискретных законов график плотности вероятности имеет ступенчатый вид, как у гистограммы на рис.2.1, и случайная величина может принимать лишь прерывистые значения (например, число зерен минералов в пробе). К таким законам относятся биномиальный, Пуассона, гипергеометрический. Законы с непрерывным распределением имеют плавный график плотности вероятности, и случайная величина может принимать любые значения в области своего существования (например, содержание компонента в руде). Сюда относятся законы нормальный, логнормальный, Стьюдента, c2, Фишера и некоторые другие. Рассмотрим наиболее часто употребляемые в геологической практике законы распределения.
2.2.2. Нормальный закон распределения
Среди всех законов распределения чаще других используют нормальный, потому что он носит предельный характер и при определенных условиях к нему приближаются многие другие законы. Нормальный закон описывается интегралом вероятности
плотность вероятности имеет следующий вид:
Кривая, выражаемая формулой (2.22), имеет симметричную форму относительно абсциссы Как следует из формул (2.21) и (2.22), нормальный закон полностью определяется двумя статистическими характеристиками: средним значением Иногда распределения бывают асимметричными (рис.2.4). Отклонение эксцесса от нуля в ту или иную сторону связано с остро- или плосковершинностью кривой распределения по отношению к нормальному распределению (рис.2.5). В частности, кривые с плоской вершиной или с несколькими максимумами имеют отрицательный эксцесс. Наиболее важное применение нормального закона распределения, как и других законов, состоит в решении задач двух типов: 1) определение вероятности появления случайной величины в заданном интервале; 2) определение интервала возможных значений случайной величины при заданной вероятности.
которому соответствует заштрихованная площадь на рис.2.6.
Наконец, иногда используется вероятность b того, что случайная величина находится за пределами интервала от а до b, тогда b = 1 – q.
Особый интерес представляет ситуация, когда размер интервалов берется равным среднеквадратичному отклонению s. В этом случае практически вся площадь под кривой плотности вероятности (точнее, 99,7 % площади) охватывается интервалом в шесть среднеквадратичных отклонений, т.е. от среднего значения вправо и влево по 3s (рис.2.7). За пределами этого интервала остается незначительная часть площади, и ею часто пренебрегают. Вычисление вероятностей сводится к нахождению определенных интегралов (2.21) или (2.23). Интеграл вероятности не интегрируется в алгебраических выражениях, поэтому для нахождения вероятности принято пользоваться специальными таблицами. Поскольку среднее значение
Интеграл вероятности F (t) и плотность вероятности f (t) стандартного нормального закона имеют вид
Таблицы значений F (t) и f (t) приведены во всех справочниках и пособиях по теории вероятностей, самые распространенные из которых «Таблицы математической статистики» [4] и «Справочник по математике для инженеров и учащихся втузов» [6]. Значения f (t) можно вычислять непосредственно по формулам (2.22) или (2.25). Большое значение имеет функция Ф(t), выражаемая интегралом:
Она характеризует вероятность q попадания случайной величины в симметричный интервал от – t до + t (рис.2.8) и связана с интегралом вероятности соотношением Ф(t) = 2 F (t) – 1. Отметим, что вероятность попадания случайной величины в интервал от нуля до + t называется функцией Лапласа. Из-за симметричности интеграл (2.26) можно представить как удвоенную функцию Лапласа:
Значения функций F (t), f (t) и Ф(t) в пределах от t = 0 до t = 3,1 с шагом аргумента 0,1 приведены в табл.2.6. Для более детального определения значений функций рекомендуются вышеупомянутые справочники [4, 6]. Поскольку функции f (t) и Ф(t) симметричны относительно t = 0, их значения при отрицательном значении t находят из табл.2.6 без учета знака. Для нахождения функции F (t) при отрицательных значениях t нужно использовать соотношение F (– t) = 1 – F (t). Например, при t = –1,7 из табл.2.6 имеем f (t) = 0,0940; Ф(t) = 0,9109; F (t) = 1 – 0,9554 = 0,0446. Таблица 2.6
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.1.100 (0.01 с.) |

 , (2.20)
, (2.20)
 (2.21)
(2.21) . (2.22)
. (2.22)
 (рис.2.3). Площадь между кривой и осью абсцисс равна единице. Ветви кривой не ограничены и уходят в плюс и минус бесконечность, сливаясь в удалении от величины
(рис.2.3). Площадь между кривой и осью абсцисс равна единице. Ветви кривой не ограничены и уходят в плюс и минус бесконечность, сливаясь в удалении от величины 
 Вероятность p того, что значение случайной величины не превысит заданное значение а (заштрихованная площадь на рис.2.2) определяется интегралом (2.20), т.е. p = F (а). Наоборот, вероятность a того, что значение случайной величины больше заданного значения а (незаштрихованная площадь на рис.2.2), равна 1 – p. Часто приходится оценивать вероятность q попадания случайной величины в заданный интервал от а до b, ее находят как интеграл:
Вероятность p того, что значение случайной величины не превысит заданное значение а (заштрихованная площадь на рис.2.2) определяется интегралом (2.20), т.е. p = F (а). Наоборот, вероятность a того, что значение случайной величины больше заданного значения а (незаштрихованная площадь на рис.2.2), равна 1 – p. Часто приходится оценивать вероятность q попадания случайной величины в заданный интервал от а до b, ее находят как интеграл: , (2.23)
, (2.23)

 и единичное среднеквадратичное отклонение (s = 1). Чтобы пользоваться такими таблицами, нужно предварительно нормировать исходные значения случайной величины х по формуле
и единичное среднеквадратичное отклонение (s = 1). Чтобы пользоваться такими таблицами, нужно предварительно нормировать исходные значения случайной величины х по формуле . (2.24)
. (2.24)

 . (2.25)
. (2.25)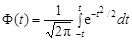 . (2.26)
. (2.26) . (2.27)
. (2.27)



