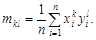Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет коэффициента корреляцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
По данным таблицы 3.1 имеем:
Тот же критерий на основе нормального закона распределения:
В обоих случаях критерий t значительно больше трех, поэтому линейная связь между содержаниями железа общего и магнетитового доказана надежно.7
3.1.3. Уравнение линейной регрессии
Если между величинами х и у установлена линейная статистическая зависимость, то представляет интерес найти ее выражение в виде уравнения прямой линии у = ах + b (где а и b – коэффициенты). Такое уравнение называется уравнением регрессии. Если величина х неслучайная, то существует одно уравнение регрессии. Если обе величины (х и у) случайные, то имеется два уравнения регрессии и можно вычислять зависимости как у от х, так и х от у. Расчет уравнения сводится к определению наиболее вероятного значения у, когда известно значение х. Опуская вывод, запишем уравнение линейной зависимости через статистические характеристики:
Аналогичный вид имеет второе уравнение зависимости х от у:
Эти уравнения пересекаются в точке средних значений Как указывалось, дисперсия случайной величины является характеристикой ее рассеяния около математического ожидания или среднего значения. Уравнение регрессии (3.12) позволяет определить еще одну остаточную дисперсию sd, которая характеризует рассеяние значений случайной величины около линии регрессии: где d i – отклонения значений случайной величины у от линии регрессии. Дисперсии Разность между ними также является дисперсией, учтенной (поглощенной) уравнением регрессии. Она называется дисперсией тренда которое можно рассматривать как разложение дисперсии Уравнение линейной регрессии позволяет решать несколько практических задач. Первое назначение уравнения описательное, потому что часто важен сам факт линейной зависимости и ее аналитическое выражение. Но наибольшая эффективность уравнения заключается в возможности прогнозирования значения одной случайной величины, если известно значение другой. Поскольку зависимость носит статистический характер, прогнозирование по уравнению (3.12) будет сопровождаться погрешностью t sd или, учитывая формулу (3.15), погрешностью
8 Пример 3.2. По условиям примера 3.1 необходимо рассчитать уравнение зависимости содержания железа магнетитового у от содержания железа общего х в руде. По данным табл.3.1 или после раскрытия скобок у = 1,080 х – 11,0. При t = 2 погрешность прогнозирования по уравнению
Из табл.3.1 имеем дисперсию Линию полученного уравнения можно нанести на график (рис.3.2). Она пересечет ось абсцисс при значении х = 11,0/1,080 = 10,2 %, что указывает на вероятное среднее содержание железа в немагнитных минералах руды. В качестве второй точки для проведения линии регрессии можно использовать средние значения Отметим, что существует и второе уравнение зависимости х от у, оно имеет вид или х = 0,893 у + 11,1, его погрешность 4,9. Линии обоих уравнений пересекаются в точке средних значений
3.1.4. Двухмерное нормальное распределение. Эллипс рассеяния
Облако точек на рис.3.1, как и во многих других случаях, в первом приближении имеет эллипсовидную форму. В ряде задач нужно знать параметры эллипса, охватывающего облако, и построить эллипс на чертеже. Идеальный эллипс возникает в том случае, когда система двух случайных величин и каждая из них в отдельности подчиняются нормальному закону распределения. Но и при заметных отклонениях от него конфигурация облака может быть охарактеризована эллипсом рассеяния. Двухмерное нормальное распределение системы двух случайных величин описывается формулой плотности вероятности В формулу входит пять статистических характеристик, рассмотренных выше. Если спроектировать облако точек на оси Ох и Оу и построить гистограммы частот величин х и у, то каждая из них подчиняется нормальному закону (рис.3.3):
Облако точек заключено внутри эллипса, выраженного уравнением где t – коэффициент вероятности. Если t будет принимать другие значения, будут построены подобные эллипсы иного размера (рис.3.4). В центре эллипса точки расположены гуще, к краям их плотность убывает. Вероятность попадания точек в эллипс при нормальном распределении с параметром (квантилью) t описывается формулой
Для построения эллипса необходимо знать положение его центра, размеры осей (полуосей) и их ориентировку по отношению к осям координат. Центр эллипса имеет координаты Его решение дает два угла a1 и a2, отличающихся друг от друга на 90°. Чтобы найти полуоси эллипса, начало координат переносят в центр эллипса, в точку откуда следует, что полуоси эллипса равны Дисперсии разброса точек
Сумма дисперсий при переносе и повороте координат не меняется. Она зависит от взаимного расположения точек в облаке и является инвариантом: Таким образом, чтобы построить эллипс рассеяния, достаточно знать координаты его центра 3.1.5. Нелинейная регрессия. Метод наименьших квадратов
Зависимости между свойствами могут быть не только линейными, но и более сложными – нелинейными и многофакторными. Для обработки любых зависимостей существует эффективный метод наименьших квадратов. Суть метода состоит в том, что изучаемая зависимость аппроксимируется таким алгебраическим выражением (трендом), который дает наименьшее расхождение с наблюдаемыми значениями. Пусть значения величины у нелинейно зависят от значений величины х (точки на рис.3.5). Нужно подобрать такую функцию f (x),в которой отклонения между фактическими yi и расчетными (теоретическими) у т = f (x) значениями будут наименьшими. Отклонения d i = yi – y т могут быть положительными и отрицательными. Главный принцип метода заключается в требовании, чтобы сумма квадратов всех отклонений от линии зависимости была минимальной:
Вид аппроксимирующей функции f (x)должен быть задан либо на основании теоретических соображений (например, гиперболическая зависимость плотности руды от ее состава в примере 1.3), либо путем эмпирического подбора. Например, в качестве функции f (x) могут быть использованы полином порядка p: f (x) = = a 0 + a 1 x + a 2 x 2 + … + apxp; синусоида f (x) = a sin(bx + c);показательная функция f (x) = a e bx и др. В каждой функции присутствуют постоянные коэффициенты a, b, c (их число зависит от вида функции), значения которых заранее не известны и которые определяют положение кривой на графике (рис.3.5). Следовательно, и сумма квадратов отклонений также зависит от значений коэффициентов, т.е. является их функцией: Чтобы найти минимум этой функции, нужно взять частные производные по неизвестным коэффициентам и приравнять их нулю: В результате будет получена система уравнений, в которой число уравнений равно числу неизвестных. Решая эту систему, найдем искомые коэффициенты a, b, c … Когда коэффициенты в функции f (x)определены, можно найти расчетные значения y т = f (x) для каждого xi и сравнить их с фактическими yi, т.е. найти отклонения d i = yi – y т. Далее вычисляют дисперсии отклонений: и, наконец, определяют корреляционное отношение:
которое заключено в интервале от нуля до единицы (0 £ h £ 1) и характеризует степень нелинейной зависимости между величинами х и у. Чем ближе h к единице, тем сильнее зависимость. При h = 0 связь отсутствует.
Зная дисперсию исходных данных Рассмотренная схема обработки данных применима к исследованию линейных и нелинейных, однофакторных и многофакторных зависимостей. В частном случае простой линейной зависимости y = ax + b использование метода наименьших квадратов дает уравнение регрессии (3.12), а корреляционное отношение по абсолютной величине совпадет с коэффициентом корреляции. 3.1.6. Применение метода наименьших квадратов к параболической зависимости
Имеется нелинейная зависимость (рис.3.6). Требуется рассчитать нелинейную параболическую зависимость по методу наименьших квадратов. Уравнение параболы имеет вид y = ax 2 + bx + c. (3.27) Следовательно, для каждой точки графика справедливо соотношение (см. рис.3.5) Из этого выражения найдем отклонения d i и сумму квадратов отклонений, которая является функцией y от неизвестных коэффициентов a, b, c: y(a, b, c) =
Чтобы отыскать минимум функции y(a, b, c), необходимо найти частные производные от функции по неизвестным a, b, c и приравнять производные нулю:
После раскрытия скобок и преобразования получим систему трех уравнений с тремя неизвестными Заметим, что
Разделим левые и правые части всех уравнений системы (3.28) на n и запишем систему через смешанные начальные моменты: am 40 + bm 30 + cm 20 = m 21; am 30 + bm 20 + cm 10 = m 21; (3.29) am 20 + bm 10 + c = m 01. Для того чтобы найти коэффициенты a, b, c в уравнении параболы (3.27), нужно вычислить все моменты, входящие в систему (3.29), и решить ее. Система уравнений (3.29) линейна относительно неизвестных a, b, c,что существенно облегчает расчеты. Нередко встречаются такие зависимости (например, гиперболические), которые приводят к сложной нелинейной системе, которую нельзя решить алгебраическим путем. Подобные системы решают методом последовательных приближений. 8 Пример 3.3. По простиранию рудного тела от произвольной точки отсчета на расстоянии хi от нее измерена мощность yi (рис.3.6, табл.3.2). Требуется рассчитать параболическую зависимость мощности линзообразного рудного тела. Порядок расчета начальных моментов приведен в табл.3.2, последняя строка которой содержит данные, необходимые для составления системы уравнений (3.29): 33076 a + 2079 b + 139,5 c = 178,8; 2079 a + 139,5 b + 10,5 c = 15,61; 139,5 a + 10,5 c + c = 1,575. Решая систему, найдем коэффициенты a = –0,0270; b = 0,532; c = = –0,242. Следовательно, уравнение аппроксимирующей параболы имеет вид у т = –0,0270 х 2 + 0,532 х – 0,242.
Таблица 3.2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.123.194 (0.011 с.) |




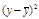


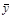


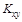
 = 29,1;
= 29,1;  = = 166,43;
= = 166,43;  = 201,32; s х = 12,90; s у = 14,19; Кху = 179,75; r = 179,75/(12,90×14,19) = 0,982. Вычисленный коэффициент корреляции r = 0,982 близок к единице, следовательно, связь между свойствами сильная и положительная. Чтобы убедиться в реальности связи, вычислим критерий Стьюдента по формулам (3.6):
= 201,32; s х = 12,90; s у = 14,19; Кху = 179,75; r = 179,75/(12,90×14,19) = 0,982. Вычисленный коэффициент корреляции r = 0,982 близок к единице, следовательно, связь между свойствами сильная и положительная. Чтобы убедиться в реальности связи, вычислим критерий Стьюдента по формулам (3.6):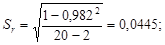
 .
.
 .
. . (3.12)
. (3.12) . (3.13)
. (3.13) (3.14)
(3.14) и
и  . (3.15)
. (3.15) В некоторых публикациях ее называют дисперсией закономерной изменчивости, противопоставляя случайной остаточной дисперсии. Между тремя дисперсиями существует соотношение
В некоторых публикациях ее называют дисперсией закономерной изменчивости, противопоставляя случайной остаточной дисперсии. Между тремя дисперсиями существует соотношение , (3.16)
, (3.16) где t – коэффициент вероятности. Чем больше коэффициент корреляции по абсолютной величине, тем меньше погрешность прогнозирования. Для надежного прогнозирования необходимо использовать лишь такие зависимости, у которых коэффициент корреляции больше 0,87.
где t – коэффициент вероятности. Чем больше коэффициент корреляции по абсолютной величине, тем меньше погрешность прогнозирования. Для надежного прогнозирования необходимо использовать лишь такие зависимости, у которых коэффициент корреляции больше 0,87.
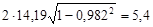 . Поэтому можно записать у = 1,080 х – 11,0 ± 5,4.
. Поэтому можно записать у = 1,080 х – 11,0 ± 5,4.
 = = 201,32 – 7,18 = 194,14. Приняв
= = 201,32 – 7,18 = 194,14. Приняв 
 . (3.17)
. (3.17)


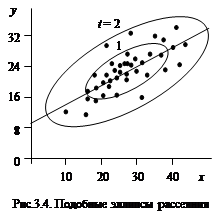
 , (3.18)
, (3.18)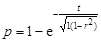 . (3.19)
. (3.19) . (3.20)
. (3.20) и поворачивают координатные оси на угол a1 или a2. Обозначим новые оси координат u и v, тогда уравнение эллипса (3.18) приобретает канонический вид:
и поворачивают координатные оси на угол a1 или a2. Обозначим новые оси координат u и v, тогда уравнение эллипса (3.18) приобретает канонический вид: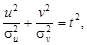 (3.21)
(3.21) и
и  .
. и
и  в новой системе координат связаны с дисперсиями
в новой системе координат связаны с дисперсиями 

 (3.22)
(3.22) (3.23)
(3.23)



 (3.24)
(3.24) (3.25)
(3.25) (3.26)
(3.26) , можно по их разности найти еще одну дисперсию
, можно по их разности найти еще одну дисперсию  которая характеризует изменчивость расчетных значений у т и может быть названа закономерной. Приняв общую дисперсию за 100 %, можно найти соотношение между
которая характеризует изменчивость расчетных значений у т и может быть названа закономерной. Приняв общую дисперсию за 100 %, можно найти соотношение между 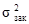 в процентах.
в процентах. .
.






 (3.28)
(3.28)
 Для удобства последующей записи введем смешанные начальные моменты:
Для удобства последующей записи введем смешанные начальные моменты: