
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автокорреляция в остатках. Критерий Дарбина-УотсонаСодержание книги
Поиск на нашем сайте
При моделировании временных рядов нередко встречается ситуация, когда остатки содержат тенденцию или циклические колебания. Это свидетельствует о том, что каждое следующее значение остатков зависит от предшествующих. В этом случае говорят о наличии автокорреляции остатков. Автокорреляция остатков мб вызвана несколькими причинами, имеющими различную природу: 1) связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака. 2) проблема в формулировке модели. Модель м-т не включать фактор, оказывающий существенное воздействие на результат, влияние которого отражается в остатках, вследствие чего последние м-т оказаться автокорреллированными. Очень часто этим фактором является фактор времени t. в качестве таких существенных факторов м-т выступать лаговые значения переменных, включенных в модель. Либо модель не учитывает несколько второстепенных факторов, совместное влияние которых на результат существенно ввиду совпадения тенденций их изменения или фаз циклических колебаний. От истинной автокорреляции остатков следует отличать ситуации, когда причина автокорреляции заключается в неправильной спецификации функциональной формы модели. Существует 2 наиболее распространенных метода определения автокорреляции остатков. 1) построение графика зависимости остатков от времени и визуальное определение наличия отсутствия автокорреляции. 2) использование критерия Дарбина – Уотсона и расчет величины d. Значение критерия Дарбина-Уотсона указывается наряду с коэффициентом детерминации, значениями t и F критериев. Соотношение между критерием Дарбина-Уотсона и коэффициентом автокорреляции остатков первого порядка: d≈2*(1-rε1). Т.о., если в остатках существует полная положительная автокорреляция и rε1=1, то d=0. Если в остатках полная отрицательная автокорреляция, то rε1=-1 и d=4. Если автокорреляция остатков отсутствует, то rε1=0 и d=2. Следовательно, 0≤d≤4. Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий:1)выдвигается гипотеза Но об отсутствии автокорреляции остатков. Альтернативные гипотезы Н1 и Н* состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. 2)по специальным таблицам определяются критические значения критерия Дарбина-Уотсона dL и dU для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости α. По этим значениям числовой промежуток [0;4] разбивают на 5 отрезков. Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняет гипотезу 38. Модели с лаговыми переменными (основные понятия, определения и направления использования) Рассмотрим модель с распределенным лагом в ее общем виде в предложении, что максимальная величина лага конечна: yt=a+b0*x1+b1*xt-1+…+bp*xt-p+ εt. Эта модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной x1 то это изменение будет влиять на значения переменной y в течение l следующих моментов времени.Коэффициент регрессии b0 (краткосрочный мультипликатор) при переменной xt характеризует среднее абсолютное изменение yt при изменении xt на 1ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора x. Еще две важные характеристики модели множественной регрессии: величина среднего лага и медианного лага. Средний лаг определяется по формуле средней арифметической взвешенной: l = Σj*βj и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора, тогда как высокое его значение говорит о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени. Медианный лаг – это величина лага, для которого Σβj≈0,5. Это тот период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат. Применение обычного МНК к таким моделям в большинстве случаев затруднительно по следующим причинам: 1)текущие и лаговые значения независимой переменной, как правило, тесно связаны друг с другом. Тем самым оценка параметров модели проводится в условиях высокой мультиколлинеарности факторов. 2) при большой величине лага снижается число наблюдений, по которому строится модель. И увеличивается число е факторных признаков. Это ведет к потере числа степеней свободы в модели. 3) в моделях с распределенным лагом часто возникает проблема автокорреляции остатков. Вышеуказанные обстоятельства приводят к значительной неопределенности относительно оценок параметров модели, снижению их точности и получению неэффективности оценок. 39. Аддитивная модель сезонности Шаг1. Выравнивание исх ряда методом скользящей средней. Для этого:1-проссумируем ур-ни ряда последовательно за каждые 4кв со сдвигом на 1 момент времени; 2-разделив получен суммы на 4, найдем скользящие средние. Полученные т.о. выравнен знач не содержат сезон компоненты. 3-приведем эти знач в соответствие с фактич моментами времени. Для этого найдём средн знач из 2х последовательных. Шаг6. Расчет относит или абсолютн ошибок. Если получен знач ошибок не содержат автокоррел или м/заменит исх ур-ни ряда и в далнейш использ времен ряд ошибок для анализа взаимосвязи исх ряда и др.времен рядов. 40 Мультипликативная модель сезонности Шаг1. Выравнивание исх ряда методом скользящей средней. Для этого:1-проссумируем ур-ни ряда последовательно за каждые 4кв со сдвигом на 1 момент времени; 2-разделив получен суммы на 4, найдем скользящие средние. Полученные т.о. выравнен знач не содержат сезон компоненты. 3-приведем эти знач в соответствие с фактич моментами времени. Для этого найдём средн знач из 2х последовательных. Шаг4. Аналитич выравнивание уровней (T*E) и расчет знач трендовых компонент с использованием получен ур-ия тренда. Определим T. Для этого рассчитаем параметры лин тренда, используя ур-ни:
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.126.241 (0.009 с.) |

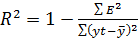 => аддитивная модель объясняет 97% общей вариации уровней времен ряда.
=> аддитивная модель объясняет 97% общей вариации уровней времен ряда.
 подставляя в получен ур-ие знач t, найдем тренд.компоненту для кажд момента времени.
подставляя в получен ур-ие знач t, найдем тренд.компоненту для кажд момента времени.


