
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка параметров уравнения парной регрессии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Оценка параметров уравнения парной регрессии. Эконометрические модели делятся на линейные и нелинейные. Построение линейной регрессии сводится к оценке ее параметров – а и b. Оценка параметров линейной регрессии могут быть найдены разными методами.Можно обратиться к полю корреляции и,выбрав на графике две точки,провести через них прямую линию,затем по графику найти значения параметров.Параметр a определим как точку пересечения линии регрессии с осью oy,а параметр b оценим исходя из угла наклона линии регрессии как dy/dx,где dy – приращение результата y,а dx – приращение фактора x,т.е.
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК) Линейная модель парной регрессии: у=bх+a+E b - коэф-т регрессии, показывающий, как изменится у при изменении х на единицу a - это свободный член, расчетная величина, содержания нет. E - это остаточная компонента, т.е. случайная величина, независимая, нормально распределенная, мат ожид = 0 и постоянной дисперсией. Присутствие e в модели свидетельствует о том, что функциональной зависимости м\у у и х нет. На изменение у оказывает влияние не только фактор х, но и какие-то др не учтенные моделью факторы. Первой задачей регрессионного анализа явл получение значения параметров a и b. Найт этои параметры мы не можем (пришлось бы обследовать ген совокупность), поэтому находим выборочные оценки этих параметров. ŷ = a + b x Для нахождения выборочных оценок используем метод НК
решением системы нормальных уравнений будет:
выборочные оценки для ур-я (1) очевидно, что мин регрессия будет иметь место только в том случае, если В этом случае зависимость отсутствует.
Нелинейная модель. уравнение зависимости между Уи Х может быть представлено степенной функцией У от Х, Для оценки параметров в этих случаях метод наименьших квадратов можно применять после логарифмирования, либо после введения новой переменной. Для показательной функции: ln y=ln a+x ln b Y α β Y = α + х β Þ а = еα; b=еβ Для степенной функции ln y=ln a+b ln x Y α X Y = α + β X Для гиперболической функции у=а+b/x 1/х=Х У=а+bХ Показатели тесноты связи в моделях парной регрессии. Значимость влияния фактора х на результат у, т.е тесноту связи оценивают показатели корреляции. Для колич. оценки тесноты используют коэффициент пар. лин. корреляции:
ryx>0 – связь прямая ryx<0 – связь обратная ryx изменяется в [-1;1] |r|<0,3 – связь слабая |r|>0,7 – связь тесная 0,3≤|r|≤0,7 – связь заметная ryx=rxy
Для оценки качества подбора линейной ф-ции рассчитывается коэф. детерминации (квадрат коэф.корреляции),хар-т долю дисперсии результативного признака, объясняемую регрессией в общ дисперсии результативного признака. r2=G2объясн/G2общ. 1-r2 – характеризует долю дисперсии рез-та вызван влиянием неучтен в модели факторов. Пример: r2=0,95 => вариация результата на 95% обусловлена вариацией данного фактора; на 5% обусловлена факторами, не включенными в модель. Для оценки влияния факторов на рез-т вычисляют коэффициент эластичности: 1) Для линейной функции: 2) Для нелинейной функции: Интерпретация: Э=3 => при изменении фактора на 1%, результат изменяется на 3% от среднего значения.
Статистический анализ достоверности модели парной регрессии Оценка значимости ур. регрессии в целом производится с помощью F-критерия Фишера, которому предшествует дисперсионный анализ, применяемый как вспомогат. ср-во для изучения качества регрессионной модели. Схема представлена в таблице. n- число наблюдений; m- число параметров при «х» В парной регрессии m=1
F=Dфакт/Dост Fтабл (α;k1;k2) k1=m k2=n-2 Fфакт>Fтабл => гипотеза H0 отклоняется Также, значение F-критерия можно найти через равенство: F=(n-2)*r2/(1-r2)
Специфика временного ряда Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов. Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов. Применение традиционных методов корреляционно-регрессионного анализа для изучения причинно следственных зависимостей переменных, представленных в форме временных рядов, может привести к ряду серьезных проблем, возникающих как на этапе построения, так и на этапе анализа эконометрических моделей. В первую очередь эти проблемы связаны со спецификой временных рядов как источника данных в эконометрическом моделировании. Предполагается, что в общем случае каждый уровень временного ряда содержит три основные компоненты: тенденцию (Т), циклические или сезонные колебания (S) и случайную компоненту (E). Если временные ряды содержат сезонные или циклические колебания, то перед проведением дальнейшего исследования взаимосвязи необходимо устранить сезонную или циклическую компоненту из уровней каждого ряда, поскольку ее наличие приведет к завышению истинных показателей силы и связи изучаемых временных рядов в случае, если оба ряда содержат циклические колебания одинаковой периодичности, либо к занижению этих показателей в случае, если сезонные или циклические колебания содержит только один из рядов или периодичность колебаний в рассматриваемых временных рядах различна. Устранение сезонной компоненты из уровней временных рядов можно проводить в соответствии с методикой построения аддитивной и мультипликативной моделей. Если рассматриваемые временные ряды имеют тенденцию, коэффициент корреляции по абсолютной величине будет высоким, что в данном случае есть результат того, что х и у зависят от времени, или содержат тенденцию. Для того чтобы получить коэффициенты корреляции, характеризующие причинно следственную связь между изучаемыми рядами, следует избавиться от так называемой ложной корреляции, вызванной наличием тенденции в каждом ряде. Влияние фактора времени будет выражено в корреляционной зависимости между значениями остатков et за текущий и предыдущие моменты времени, которая получила название «автокорреляция в остатках». 32. Автокорреляция уровней временного ряда При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда. Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Коэффициент корреляции имеет вид:
В качестве переменой x рассмотрим ряд
Коэффициент автокорреляции первого порядка измеряет зависимость между соседними уровнями ряда t и t-1, т.е. при лаге 1. Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями уt и y t-2 и определяется по формуле:
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Некоторые авторы считают целесообразным для обеспечения статистической достоверности коэффициентов корреляции использовать правило – максимальный лаг должен быть не больше (n/4). Отметим два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной (или близкой к линейной) связи текущего и предыдущего уровней ряда. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю. Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага называется коррелограммой. Анализ автокорреляционной функции и графика можно выявить структуру ряда. Если наиболее высоким оказался коэффициент автокорреляции 1го порядка, то ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент порядка Оценка параметров уравнения парной регрессии. Эконометрические модели делятся на линейные и нелинейные. Построение линейной регрессии сводится к оценке ее параметров – а и b. Оценка параметров линейной регрессии могут быть найдены разными методами.Можно обратиться к полю корреляции и,выбрав на графике две точки,провести через них прямую линию,затем по графику найти значения параметров.Параметр a определим как точку пересечения линии регрессии с осью oy,а параметр b оценим исходя из угла наклона линии регрессии как dy/dx,где dy – приращение результата y,а dx – приращение фактора x,т.е.
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК) Линейная модель парной регрессии: у=bх+a+E b - коэф-т регрессии, показывающий, как изменится у при изменении х на единицу a - это свободный член, расчетная величина, содержания нет. E - это остаточная компонента, т.е. случайная величина, независимая, нормально распределенная, мат ожид = 0 и постоянной дисперсией. Присутствие e в модели свидетельствует о том, что функциональной зависимости м\у у и х нет. На изменение у оказывает влияние не только фактор х, но и какие-то др не учтенные моделью факторы. Первой задачей регрессионного анализа явл получение значения параметров a и b. Найт этои параметры мы не можем (пришлось бы обследовать ген совокупность), поэтому находим выборочные оценки этих параметров. ŷ = a + b x Для нахождения выборочных оценок используем метод НК
решением системы нормальных уравнений будет:
выборочные оценки для ур-я (1) очевидно, что мин регрессия будет иметь место только в том случае, если В этом случае зависимость отсутствует.
Нелинейная модель. уравнение зависимости между Уи Х может быть представлено степенной функцией У от Х, Для оценки параметров в этих случаях метод наименьших квадратов можно применять после логарифмирования, либо после введения новой переменной. Для показательной функции: ln y=ln a+x ln b Y α β Y = α + х β Þ а = еα; b=еβ Для степенной функции ln y=ln a+b ln x Y α X Y = α + β X Для гиперболической функции у=а+b/x 1/х=Х У=а+bХ
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 2908; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

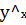 = a+ bx
= a+ bx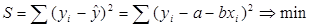
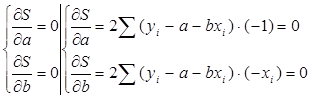

 , если хi совпадает с
, если хi совпадает с  .
.
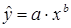 , показательной
, показательной 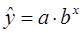 , гиперболической
, гиперболической  и д.р.
и д.р.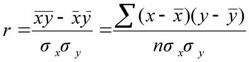
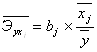

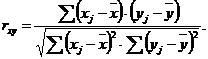
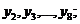 в качестве переменной y – ряд
в качестве переменной y – ряд 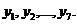 Тогда коэффициент автокорреляции первого порядка:
Тогда коэффициент автокорреляции первого порядка: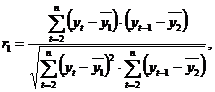 где
где 
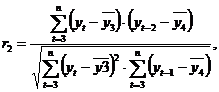 где
где 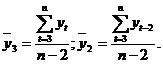
 – то содержит циклические колебания с периодичностью в
– то содержит циклические колебания с периодичностью в 


