
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гетероскедастичность – понятие, проявление и меры устраненияСодержание книги
Поиск на нашем сайте
Дисперсия - среднее арифметическое из квадратов отклонений наблюденных значений (x1, x2,...,xn) случайной величины от их среднего арифметического. Гомоскедастичность остатков означает, что для каждого значения фактора xj остатки
а — дисперсия остатков растет по мере увеличения х; б — дисперсия остатков достигает максимальной величины при средних значениях переменной х и уменьшается при минимальных и максимальных значениях х; в — максимальная дисперсия остатков при малых значениях х и дисперсия остатков однородна по мере увеличения значений х.
Наличие гомоскедастичности или гетероскедастичности можно видеть и по графику зависимости остатков
Гетероскедастичность будет сказываться на уменьшении эффективности оценок
При этом величина
При минимизации этой суммы квадратов отдельные ее слагаемые взвешиваются: наблюдениям с наибольшей дисперсией придается пропорционально меньший вес. Задача состоит в том, чтобы определить величину При малом объеме выборки для оценки нарушения гомоскедастичности можно использовать метод Гольдфельда-Квандта, который включает: 1.Упорядочение наблюдений n по мере возрастания переменной х. 2. Исключения из рассмотрения центральных наблюдений C; при этом 3. Разделение совокупности 4. Определение остаточной суммы квадратов для обеих групп Вопрос 23 ОМНК при построении модели регрессии Дисперсия остатков гомоскедостична, если для каждого фактора xi остатки Ei имеют одинаковую дисперсию. Если это условие МНК не соблюдается, то имеет место гетероскедостичноть. При нарушении гомоскедостичности и наличии автокорреляции ошибок необходимо традиционный метод наименьших квадратов заменить обобщенным МНК. Обобщенный метод применяется к преобразованным данным и позволяет получать оценки которые обладают свойством несмещенности. Предположим, что среднее значение остаточных величин = 0, а дисперсия пропорциональна величине ki σE2=ki*σ2 То есть дисперсия остатков (σE2) при конкретном i значении фактора σ2 – постоянная дисперсия ошибки при соблюдении предпосылки о гососкедостичности остатков ki – коэф. Пропорциональности, меняющийся с изменением величины фактора и обуславливающий неоднородность дисперсии, при этом σ2 - неизвестна, а в отношении величины Ki выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности, т.е. неоднородности остатков. Тогда уравнение yi=a+b*xi+Ei примет вид: y=a+b*x+ в этой модели остаточные величины гетероскедостичны. Предположим отсутствуе автокорреляции остатков и перейдем к уравнению с гомоскедастичными остатками, поделив все переменные зафискированные в ходе I наблюдения на Тогда дисперсия остатков будет величиной постоянной, то есть перейдем к уравнению регрессии в следующем виде: yi/ Где матрица исходных данных для результативного признака будет иметь вид:
y/ По отношению к обычной регрессии уравнение с новыми преобразованными переменными представляет собой взвешенную регрессию с весами 1/ Поэтому оценка параметров нов уравнения с преобразованными переменными приводит к взвешенному МНК, для кот необходимо минимизировать сумму квадратов отклонений вида:
Мы получим след систему норм уравнений: 1.∑yi/Ki=a*∑1/Ki+b*∑xi/Ki 2.∑yi*xi/Ki=a*∑xi/Ki+b*∑xi2/Ki Аналогичный подход возможен и для уравнений множественной регрессии y=a+b1x1+b2x2+E, для которой дисперсия остаточных величин пропорциональна Ki2, то есть Ei2=ki2* σ2 Тогда модель примет вид: y=a+b1x1+b2x2+E*ki Чтобы получить уравнение с гомоскедостичными остатками перейдем к новым преобразованным переменным разделив все члены исходного уравнения на коэф пропорциональности K. Уравнение с преобразованными переменными будет иметь следующий вид: Y/ki = a/ki + b1*x1/ki + b2*x2/ki + Ei Дальше как в обычном МНК При использовании этого метода мы вынуждены переходить к относительным величинам, которые существенно снижают вариацию фактора и соответственно уменьшают дисперсию ошибки, т.е. это наиболее простой способ учета гетероскедостичности в регрессионных моделях.
Вопрос 24 Общее понятие о системах уравнений, используемых в эконометрике
При использовании отдельных уравнений регрессии для экономических расчетов предполагает что факторы можно изменять независимо друг от друга. Однако изменение одного из факторов ведет к изменениям во всей системе взаимосвязанных признаков. Поэтому используют системы так называемых одновременных уравнений, которые также называются структурными уравнениями. Система уравнений может быть построена разными способами: 1) Систиема независимых уравнений: когда каждая зависимая переменная У рассматривается как функция одного и того же набора факторов Х. Y1=a11x1+a12x2+…a1nxn+E1 Y2=a21x1+a22x2+…+a2nxn+E2 … Ym=am1x1+am2x2+…+amnxn+En
Каждое независимое уравнение системы рассматривается как самостоятельное. Для нахождения параметров в уравнениях используется МНК. (пример - модель эконом эффективности с/х производства.)
2) Система рекурсивных уравнений (когда зависимая переменная одного уравнения выступает в виде фактора Х в другом уравнении). Y1=A11X1+A12X2+…+A1nXn+E1 …
Каждое уравнение может быть рассмотрено самостоятельно. Параметры определяются методом МНК. (пример - модель производительности труда и фондоотдачи) 3) Система взаимозависимых уравнений (наибольшее распространение).В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, другие - в правую. Y2=B21Y1+B22Y3+…+B2mYm+1+A21X1+…+A2nXn+E2 …
Вопрос 25 Виды переменных в системах взаимозависимых уравнений Система совместных одновременных уравнений или структурная форма модели обычно содержит эндогенные и предопределенные переменны. Эндогенные – зависимые переменные, число которых обычно равно числу уравнений в системе. Предопределенные – которые влияют на эндогенные переменные, но не зависят от них. Они бывают 2х видов: 1. Экзогенные – которые определены вне системы; 2. Лаговые – эндогенные переменные в предыдущий момент времени. Yt=a11x1+yt-1 Yt-1 – предопределенная переменная Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значение эндогенной переменной. Поэтому в качестве экзогенных переменных целесообразно выбирать такие, которые могут быть объектом регулирования. Управляя этими переменными можно заранее иметь целевые значения эндогенных переменных. Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции модели. Экономические переменные могут быть экзогенными в одной модели и эндогенными в другой модели. Внеэкономические переменные (например, климатические условия) – всегда экзогенные.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 808; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.137.10 (0.009 с.) |

 имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетеродастичности можно наглядно видеть из поля корреляции.
имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетеродастичности можно наглядно видеть из поля корреляции.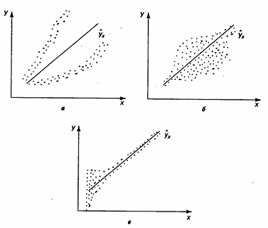
 .
. Большая дисперсия
Большая дисперсия  .В частности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии
.В частности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии  , предполагающей единую дисперсию остатков для любых значений фактора. Практически при нарушении гомоскедастичности мы имеем неравенства:
, предполагающей единую дисперсию остатков для любых значений фактора. Практически при нарушении гомоскедастичности мы имеем неравенства: или
или 
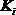 может меняться при переходе от одного значения фактора
может меняться при переходе от одного значения фактора  к другому. Это означает, что сумма квадратов отклонений для зависимости
к другому. Это означает, что сумма квадратов отклонений для зависимости 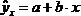 при наличии гетероскедастичности должна иметь вид:
при наличии гетероскедастичности должна иметь вид: 
 где p – число оцениваемых параметров.
где p – число оцениваемых параметров. на две группы (с малыми и большими значениями фактора х) и определение по каждой из групп уравнений регрессии.
на две группы (с малыми и большими значениями фактора х) и определение по каждой из групп уравнений регрессии. и
и  и нахождение их отношения:
и нахождение их отношения:  При выполнении нулевой гипотезы о гомоскедастичности отношение R будет соответствовать F-критерию с
При выполнении нулевой гипотезы о гомоскедастичности отношение R будет соответствовать F-критерию с  степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табл. значение F-критерия, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин.
степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табл. значение F-критерия, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин. *Ei
*Ei = a/
= a/ 
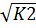

 =f(x/
=f(x/  Σ(yi-a+b*xi)2 min
Σ(yi-a+b*xi)2 min


