
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 26. Структурная и приведенная формы модели.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Структурная форма модели также называется системой взаимозависимых уравнений, или системой совместных, одновременных уравнений. y1 = b12*y2 + b13*y3 + … + b1n*yn + a11*x1 + a12*x2 + … + a1m*xm + e1 y2 = b21*y1 + b23*y3 + … + b2n*yn + a21*x1 + a22*x2 + … +a2m*xm + e2 ……………………………………………………….. yn = bn1*y1 + bn2*y2 + … + bnn-1*yn-1 + an1*x1 + an2*x2 + … + anm*xm + e2 Каждое уравнение такой системы не может рассматриваться самостоятельно. Содержит эндогенные и экзогенные переменные. Эндогенные это y. Это зависимые переменные. Их число равно числу уравнений. Экзогенные это x. Это предопределенные переменные, влияющие на эндогенные, но не зависящие от них. Простейшая форма модели: y1 = b12*y2 + a11*x1 + e1 y2 = b21*y1 + a22*x2 + e2 СФМ позволяет увидеть влияние любой экзогенной переменной на значения эндогенной переменной. bi и aj называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня, т.е. под х подразумевается х – хср., а под у подраз. у-уср. Поэтому свободный член в каждом уравнении отсутствует. Для определения структурных коэффициентов МНК не подходит. СФМ переводят в ПФМ. ПФМ это система линейных функций эндогенных переменных от экзогенных. y1 = d11*x1 + d12*x2 + … + d1m*xm y2 = d21*x1 + d22*x2 + … + d2m*xm ………………………………. yn = dn1*x1 + dn2*x2 + … + dnm*xm di – коэффициенты ПФМ Коэффициенты ПФМ – это нелинейные функции коэффициентов СФМ.
Для СФМ y1 = b12*y2 + a11*x1 y2 = b21*y1 + a22*x2 ПФМ имеет вид: y1 = d11*x1 + d12*x2 y2 = d21*x1 + d22*x2 в которой y2 = y1 – a11x1 / b12 Тогда СФМ будет выглядеть так: y2 = y1 – a11*x1 / b12 y2 = b21*y1 + a22*x2 Отсюда следует равенство: y1 – a11*x1 / b12 = = b21*y1 + a22*x2 Или: y1 – a11*x1 = b12*b21*y1 + b12* a22*x2 Или: y1 = (a11 / (1 - b12*b21))* x1 + (b12* a22 / (1 - b12*b21))* x2 Таким образом: y1 = d11*x1 + d12*x2 d11 = a11 / (1 - b12*b21); d12 = b12* a22 / (1 - b12*b21) ПФМ хотя и позволяет получить значение эндогенной переменной через значение экзогенной, но аналитически уступает СФМ, т.к. в ней отсутствуют оценки взаимосвязи между эндогенными переменными. Вопрос 27. Проблема идентификации. Порядковое условие идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели. Проблема идентификации – это проблема, возникающая при переходе от ПФМ к СФМ (от приведенной к структурной форме модели). Она связана с тем, что число структурных коэффициентов в СФМ и ПФМ м.б. различно. СФМ в полном виде, состоящая из n эндогенных и m экзогенных переменных, содержит n(n-1+m ) параметров. ПФМ в полном виде содержит nm параметров. Когда число коэффициентов ПФМ в полном виде меньше числа коэффициентов СФМ в полном виде, отсутствует единственность решения, то есть, n(n-1+m ) параметров СФМ не могут быть однозначно определены из nm параметров ПФМ. Для получения единственно возможного решения для СФМ, необходимо уменьшить число коэффициентов СФМ следующими способами: · Предположить, что некоторые структурные коэффициенты СФМ равны 0 (ввиду слабой взаимосвязи признаков с эндогенной переменной у). · Приравнять некоторые коэффициенты друг к другу (путем предположений, что их воздействие на эндогенную переменную одинаково). Также на структурные коэффициенты могут накладываться ограничения вида bij + aij = 0. СФМ делятся на 3 вида: · Идентифицируемые. Число коэффициентов СФМ = числу коэффициентов ПФМ · Неидентифицируемые. Число коэф. СФМ > числа коэф. ПФМ. СФМ в полном виде всегда неидентифицируема. · Сверхидентифицируемые. Число коэф. СФМ < числа коэф. ПФМ. СФМ представляет собой систему совместных уравнений. СФМ считается идентифицируемой, если каждое уравнение в ней идентифицируемо. Если хотя бы одно неидент., вся модель неидент. Если хотя бы одно сверхидент., то вся модель сверхидент. Для оценки параметров СФМ система д.б. идентифицируема или сверхидентиф. Порядковое условие идентификации: Для того, чтобы уравнение было идентифицируемо, нужно, чтобы число предопределенных (экзогенных) переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного. Пусть Н – число эндогенных переменных в j-м уравнении; D – число экзогенных переменных, которые содержатся в системе, но не входят в него. Тогда условие идентифицируемости модели можно записать в виде счетного правила: · D + 1 = H – уравнение идентиф. · D + 1 < H – уравнение неидентиф. · D + 1 > H – уравнение сверхидентиф. Это правило отражает необходимое, но недостаточное условие идентификации. Вопрос 28. Ранговое условие идентификации. Порядковое условие является необходимым, но недостаточным условием идентификации. Существует также достаточное условие. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой неравен 0, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного. Возможна ситуация, когда порядковое условие выполняется для каждого уравнения системы, а определитель матрицы названных коэффициентов равен 0. В этом случае выполняется лишь необходимое, но недостаточное условие. Пусть Н – число эндогенных переменных в j-м уравнении; D – число экзогенных переменных, которые содержатся в системе, но не входят в него. Пусть дана следующая СФМ: y1 = b12*y2 + b13*y3 + a11*x1 + a12*x2 y2 = b21*y1 + a22*x2 + a23*x3 + a24*x4 y3 = b31*y1 + b32*y2 + a31*x1 + a32*x2 Для первого уравнения H = 3 (y1, y2, y3) и D = 2 (x3 и x4 отсутствуют). D + 1 = H, необходимое условие выдержано. Проверим достаточное условие. Составим матрицу коэффициентов.
Определитель матрицы равен 0, достаточное условие не выполняется, первое уравнение неидентифицируемо. Для второго уравнение Н = 2 (у1 и у2), D = 1 (отсутствует х1). D + 1 = Н
Определитель неравен 0, ранг матрицы = 2 (не меньше числа эндогенных переменных в системе без одной). Второе уравнение точно идентифицируемо. 29. косвенный метод наименьших квадратов: • Структурная модель преобразовывается в приведенную форму модели. • Для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты. • Коэффициенты приведенной формы модели трансформируются в параметры структурной формы модели. Алгоритм двухшагового метода наименьших квадратов: • Определяется приведенная форма модели, и находятся на ее основе оценки теоретических значений эндогенных переменных. • Определяются структурные коэффициенты модели по данным теоретических (расчетных) значений эндогенных переменных. Косвенный МНК. 30.Двухшаговый метод наименьших квадратов состоит в том, что оценивают параметры отдельного уравнения системы, а не рассматривают систему в целом. Двухшаговый метод наименьших квадратов (ДМНК) использует следующую центральную идею: на основе приведенной формы модели получают для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Затем они подставляются вместо фактических значений и применяют обычный МНК к структурной форме сверхидентифицируемого уравнения. В свою очередь, сверхидентифицируемая структурная модель может быть двух типов: либо все уравнения системы сверхидентифицируемы, либо же система содержит наряду со сверхидентифицируемыми и точно идентифицируемые уравнения. В первом случае, если все уравнения системы сверхидентифицируемые, для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений. Специфика временного ряда Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов. Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов. Применение традиционных методов корреляционно-регрессионного анализа для изучения причинно следственных зависимостей переменных, представленных в форме временных рядов, может привести к ряду серьезных проблем, возникающих как на этапе построения, так и на этапе анализа эконометрических моделей. В первую очередь эти проблемы связаны со спецификой временных рядов как источника данных в эконометрическом моделировании. Предполагается, что в общем случае каждый уровень временного ряда содержит три основные компоненты: тенденцию (Т), циклические или сезонные колебания (S) и случайную компоненту (E). Если временные ряды содержат сезонные или циклические колебания, то перед проведением дальнейшего исследования взаимосвязи необходимо устранить сезонную или циклическую компоненту из уровней каждого ряда, поскольку ее наличие приведет к завышению истинных показателей силы и связи изучаемых временных рядов в случае, если оба ряда содержат циклические колебания одинаковой периодичности, либо к занижению этих показателей в случае, если сезонные или циклические колебания содержит только один из рядов или периодичность колебаний в рассматриваемых временных рядах различна. Устранение сезонной компоненты из уровней временных рядов можно проводить в соответствии с методикой построения аддитивной и мультипликативной моделей. Если рассматриваемые временные ряды имеют тенденцию, коэффициент корреляции по абсолютной величине будет высоким, что в данном случае есть результат того, что х и у зависят от времени, или содержат тенденцию. Для того чтобы получить коэффициенты корреляции, характеризующие причинно следственную связь между изучаемыми рядами, следует избавиться от так называемой ложной корреляции, вызванной наличием тенденции в каждом ряде. Влияние фактора времени будет выражено в корреляционной зависимости между значениями остатков et за текущий и предыдущие моменты времени, которая получила название «автокорреляция в остатках». 32. Автокорреляция уровней временного ряда При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда. Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Коэффициент корреляции имеет вид:
В качестве переменой x рассмотрим ряд
Коэффициент автокорреляции первого порядка измеряет зависимость между соседними уровнями ряда t и t-1, т.е. при лаге 1. Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями уt и y t-2 и определяется по формуле:
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Некоторые авторы считают целесообразным для обеспечения статистической достоверности коэффициентов корреляции использовать правило – максимальный лаг должен быть не больше (n/4). Отметим два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной (или близкой к линейной) связи текущего и предыдущего уровней ряда. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю. Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага называется коррелограммой. Анализ автокорреляционной функции и графика можно выявить структуру ряда. Если наиболее высоким оказался коэффициент автокорреляции 1го порядка, то ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент порядка
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.011 с.) |

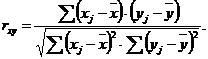
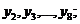 в качестве переменной y – ряд
в качестве переменной y – ряд 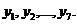 Тогда коэффициент автокорреляции первого порядка:
Тогда коэффициент автокорреляции первого порядка: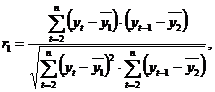 где
где 
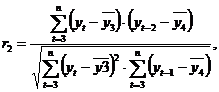 где
где 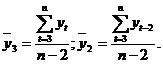
 – то содержит циклические колебания с периодичностью в
– то содержит циклические колебания с периодичностью в 


