
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметрическая и структурная оптимизацияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задачи оптимального проектирования можно разделить на два класса. К первому классу относятся задачи, в которых структура объекта считается заданной и речь идет лишь об определении числовых значений параметров, свойственных данной структуре. Такие задачи называют задачами параметрической оптимизации. К ним относятся, например, оптимизация или сочлененных стрел, или коробчатых сечений металлических конструкций, или рамных двухстоечных порталов и т.д. Во всех этих случаях тип объекта, его структура определены и в ходе оптимизации остаются неизменными (сочлененная стрела, коробчатое сечение, рамный двухстоечный портал и т.д.). Методология решения таких задач будет рассмотрена далее. Ко второму классу принадлежат задачи, в которых предметом оптимизации являются не только параметры, но и структура объекта. Примеры таких задач: выбор оптимального типа стрелового устройства для заданных условий (сочлененная стрела, прямая стрела с уравнительным полиспастом, прямая стрела с уравнительным блоком или еще какая-либо структура стрелового устройства) или оптимального типа металлической конструкции стрелы (коробчатая, трубчатая, шпренгельная и т.д.), или оптимального типа портала (рамный четырехстоечный, рамный двухстоечный: рамно-раскосный и т.д.). Такие задачи называют задачами структурной (структурно-схемной) оптимизации. Практикой выработаны два принципиально различных подхода к решению задач структурно-схемной оптимизации: метод последовательного исследования множеств и метод оптимального проектирования с автоматическим поиском схем. Согласно методу последовательного исследования множеств вначале на основе имеющегося опыта отбирают ограниченное число перспективных структур объекта, каждая из которых может быть описана своей совокупностью параметров. Далее последовательно проводят параметрическую оптимизацию каждой структуры (исследуют множество вариантов, реализующих данную структуру). Наконец, полученные оптимальные варианты сравнивают между собой и из них выбирают наилучший, принимая его за окончательное оптимальное решение задачи. При автоматическом поиске схем вместо пространства параметров, описывающего известную конкретную структуру, вводят так называемое универсальное пространство параметров (УПП), в котором можно описать любую допустимую структуру - как известную, так и неизвестную. Параметрическая оптимизация, проводимая далее в этом УПП, является одновременно структурной оптимизацией, так как в результате решения мы получаем ответ на вопрос о наилучшей структуре оптимизируемого объекта. При этом могут быть получены и изобретательские (эвристические) решения. Способ задания УПП должен позволять описать любую допустимую форму; непрерывно переходить от одной схемы к другой; локально управлять изменением формы, оставляя часть ее неизменной.
Поясним это примером. Коробчатое сечение изгибаемой конструкции (рис.2.5,а) описывается четырьмя параметрами (Х1... Х4), сечение трубы (рис.2.5б) - двумя (Х5,Х6), сечение по рис.2.5,в - шестью параметрами (Х1... Х6), образующими УПП, которое охватывает конструкции коробчатого (см. рис.2.5,а), круглого (рис.2.5,б) и произвольного сечений (заметим, что число параметров в УПП не обязательно должно быть равно сумме чисел параметров структур, объединяемых этим УПП).
Рис.2.5. Варианты описания замкнутых тонкостенных сечений
Если критерии качества (например, площадь сечения) и ограничения (например, условия прочности, включающие моменты сопротивления) выражены через Х1... Х6 (см. рис.2.5,в), то, найдя из решения задачи оптимизации оптимальные значения Х1... Х6, мы тем самым установим и оптимальную форму сечения, т.е. оптимальную структуру объекта. Так, если окажется, что в оптимальном случае Х5=0, Х6=0, то оптимальной формой будет коробчатое сечение; сочетание Х4=Х2=2Х5, Х1=Х3=2Х6 соответствует сечению круглой трубы. В более сложных случаях применение метода, основанного на УПП, сопряжено с большими техническими трудностями, в частности, требует большого объема памяти компьютера. Для оптимального проектирования подъемно-транспортных машин и их узлов более перспективным представляется метод последовательного исследования множеств. Для формирования множества вариантов объекта, на котором производится поиск оптимального решения, необходимо правильно разработать и учесть различные ограничения. Они могут быть записаны в виде системы уравнений
hк (X) = 0, k = 1,2,... К, (3.1) dl (X) ³ 0, l = 1,2,... L, (3.2)
Введение ограничений позволяет учесть реальные условия изготовления и функционирования объекта оптимизации с тем, чтобы оптимизация была физически осуществима. Задача общего вида - минимизировать q (X) при ограничениях (3.1) - (3.2) - называется задачей условной оптимизации. Задача, в которой нет ограничений, называется оптимизационной задачей без ограничений, или задачей безусловной оптимизации. Задачи оптимизации можно классифицировать в соответствии с видом функций q, hк, dl и размерностью вектора X. Задачи без ограничений, в которых Х представляет собой одномерный вектор, называются задачей с одной переменной и составляют простейший подкласс оптимизационных задач. Задачи условной оптимизации, в которых функции hк и dl являются линейными, носят название задач с линейными ограничениями. В таких задачах целевые функции могут быть либо линейными, либо нелинейными. Задачи, которые содержат только линейные функции вектора непрерывных переменных X, называются задачами линейного программирования; в задачах целочисленного программирования компоненты вектора X должны принимать только целые значения. Задачи с нелинейной целевой функцией и линейными ограничениями иногда называют задачами нелинейного программирования с линейными ограничениями. Оптимизационные задачи такого рода можно классифицировать на основе структурных особенностей нелинейных целевых функций: задачи квадратичного, дробно-линейного программирования и т.д. Деление оптимизационных задач на классы представляет значительный интерес, поскольку специфические особенности тех или иных задач играют важную роль при разработке методов их решения. Отметим, что применение методов линейного программирования оказалось плодотворным для различных задач оптимального управления нединамическими системами (оптимальное размещение оборудования, организация транспортных потоков и др.). При решении задач оптимального проектирования специальных кранов используются аналитические методы и отдельные методы нелинейного программирования.
Критерии качества
К р и т е р и й к а ч е с т в а - это функция параметров, характеризующая определенное существенное свойство объекта оптимизации. Применительно к любому варианту, фигурирующему в процессе поиска оптимального решения, необходимо уметь вычислять значения критериев качества и тем самым “измерять” качество вариантов в определенном смысле. Критерии качества могут быть заданы либо аналитическим выражением, либо замкнутым алгоритмом определения. Состав одновременно учитываемых требований к подъемно-транспортным машинам и их узлам весьма обширен и разнообразен, поэтому задачи оптимального проектирования в подъемно-транспортном машиностроении - это, как правило, многокритериальные задачи. Например, при выборе варианта схемы шарнирно-сочлененного стрелового устройства портального крана необходимо учитывать следующие показатели: геометрические (например, отклонение траектории груза от горизонтали при изменении вылета); кинематические (ускорение конца хобота при установившемся движении механизма изменения вылета); нагрузочные (характерные значения грузового неуравновешенного момента); показатели массы (масса показателей стрелового устройства и стрелового устройства в целом); энергетические (затраты энергии при работе механизма изменения вылета); стоимостные (себестоимость изготовления); экономические (приведенные затраты в сфере изготовления и в сфере эксплуатации).
В некоторых случаях в аналитические выражения для критериев качества входят накладываемые ограничения на параметры. Найти решение, оптимальное одновременно по всем показателям, в большинстве случаев невозможно. Решение, обращающее в минимум (максимум) один какой-то показатель, как правило, не обращает в минимум (максимум) другие. Поэтому приходится выбирать какой-то один критерий качества, являющийся для нас важнейшим. Такой критерий качества, характеризующий важнейшее свойство объекта, принимают за целевую функцию при оптимизации. Цель оптимизации – найти параметры Х» max q или (4.1) Х» min q. (4.2) Характер экстремума зависит от постановки задачи: например, форма (4.1) относится к оптимизации параметров загрузочного устройства из условия максимума зачерпывающей способности, а форма (4.2) – к оптимизации параметров конструкции из условия минимума ее массы. В современных условиях решающая роль принадлежит экономическим требованиям, поэтому за целевую функцию при наиболее полной постановке задачи следует принимать экономический критерий качества. В условиях, когда одни и те же требования могут быть достигнуты с помощью различных вариантов научно-технических решений, обусловливающих разные затраты общественного труда, решающим для оценки их целесообразности становится экономический эффект, оцениваемый в наиболее полной постановке по стоимости совокупной конечной общественной продукции за определенный период времени. Отметим, что в иерархии требований к объектам и соответствующих критериев качества выше экономических стоят социальные требования. Египетская пирамида считалась оптимальной не при минимуме, а при максимуме затрат материалов и человеческого (рабского) труда на возведение этого символа величия фараона. Лестницы на подъемных сооружениях прокладывают не по кратчайшей, а по наиболее удобной и безопасной трассе, что отнюдь не всегда должным образом учитывается на кранах западных фирм. Экономический критерий качества целесообразно принимать за целевую функцию в двух случаях: 1) когда экономические показатели объекта не могут быть определены с достаточной точностью из-за отсутствия необходимых данных; это часто имеет место на стадии эскизного и технического проектирования, когда для новых машин и должны определяться их оптимальные структура и параметры;
2) если у составляемых при оптимизации вариантов объектов значения экономического критерия качества различают в пределах точности их определения. Существует два способа разрешения таких противоречий. Первый способ состоит в том, чтобы принять за целевую функцию технический показатель, который в условиях сравнения вариантов может быть признан косвенным показателем экономического эффекта. Таким показателем для параметрической оптимизации крановых металлических конструкций (стрел, мостов, башен и т.д.) часто оказывается их масса. Многочисленными исследованиями установлено, что при прочих равных условиях (при фиксированных генеральных размерах кранов, марке материала, технологии изготовления) себестоимость изготовления металлических конструкций можно считать пропорциональной их массе. При структурной оптимизации такой подход является некорректным, поскольку сопоставляемые варианты предполагают различную технологию изготовления и имеют различные удельные (на единицу массы) трудоемкости изготовления. Второй способ заключается в разработке комплексного критерия качества. Комплексный критерий качества представляет собой выражение вида q = где qi - частные критерии качества (единичные показатели эффективности); p – число учитываемых частных критериев качества; q = Частные показатели качества qi целесообразно вводить в выражение (4.3) в безразмерном виде, т.е. определять по отношению к показателям базового варианта или машины-прототипа. Составление выражений целевой функции в форме (4.3) целесообразно лишь тогда, когда коэффициенты весомости ai назначены обоснованно, и теряет смысл, если они назначены произвольно. Широко распространено определение коэффициентов весомости по методу экспертных оценок. При этом рекомендуется выполнять следующие правила. Степень компетентности всех экспертов в вопросе оценки должна быть примерно одинакова. В состав экспертных комиссий не должны входить авторы изделия. Число экспертов требуется не менее семи, иначе велика вероятность принятия случайного решения. Не рекомендуется отбрасывать крайние оценки. Все эксперты должны работать независимо друг от друга по единой методике с тем, чтобы результаты были сопоставимы. Рассмотрим назначение коэффициентов весомости по одному из вариантов метода парных сравнений. Составив номенклатуру одновременно учитываемых показателей качества, эксперт сравнивает попарно значимость этих показателей, признавая один из двух показателей более важным, другой - менее важным. Такая операция вызывает меньше затруднений, чем ранжирование одновременно всех показателей. Обозначив через ai и aJ коэффициенты весомости показателей qi и qJ, записывают альтернативные качественные высказывания (ai << aJ, (ai много меньше aJ); либо ai < aJ, но не << aJ; либо ai» aJ; либо ai > aJ, но не >> aJ; либо ai >> aJ) и строят матрицу вида W =
wi J = 0 при ai << aJ; wi J = 1 при ai < aJ,но не << aJ; wi J = 2 при ai» aJ; wi J = 3 при ai > aJ, но не >> aJ; wi J = 4 при ai >> aJ. При этом, очевидно, wi J + wi J = 4; wii = w JJ = 2;
ai = ----------------- = ------------,
где в числителе сумма берется по элементам i-й строки матрицы. При этом ai = 1/p при средней значимости показателя qi; ai < 1/p при его значимости ниже средней; ai > 1/p при его значимости выше средней. Число показателей учитываемых при сравнении вариантов, не должно быть слишком велико, в противном случае коэффициенты весомости отдельных показателей приближаются к среднему значению aСР = 1/p. Можно рекомендовать p Ниже показано определение коэффициентов весомости по изложенному методу для показателей сочлененных и прямых стрел грейферных портальных кранов. Здесь mсу – масса стрелового устройства (стрелы, оттяжки, хобота, канатов, блоков); КЭ – энергетический показатель, пропорциональный затратам энергии при работе механизма изменения вылета; L - длина грузовых канатов в зоне стрелового устройства; М - наибольшее значение грузового неуравновешенного момента; w - соотношение скоростей горизонтального перемещения конца хобота при установившемся движении изменения вылета от наибольшего до наименьшего. Заготовим таблицу по форме (табл.1) для квадратной матрицы W, которую предстоит заполнить. Всем элементам главной диагонали матрицы (i = j) присваиваем значение, равное двум (wi J = 2), так как любой показатель равноценен по важности самому себе. Показатель mСУ с позиции, например, инженера-конструктора завода-изготовителя является более важным, чем грузовой неуравновешенный момент, поэтому в 4-й клетке 1-й строки эксперт записывает w14 = 4 и в 1-й клетке 4-й строки w41 = 0. По сравнению с показателем КЭ масса также представляется более важной, однако КЭ прямо связан с экономичностью работы крана, поэтому w13 = 3 и w31 = 1. Поступая далее подобным образом, эксперт заполняет всю таблицу и затем вычисляет искомые коэффициенты весомости (табл.2). Таким образом, при сопоставлении вариантов стрелового устройства надлежит пользоваться комплексным показателем вида q = 0,34 mСУ+ 0,28 КЭ + 0,20 L + 0,12M + 0,06 w. Т а б л и ц а 1
Т а б л и ц а 2
Эксперт, связанный не с проектированием и изготовлением, а с эксплуатацией крана, по-видимому, иначе оценит сравнительную значимость конкретных показателей и получит иные коэффициенты весомости. Окончательный вид показателя q может быть составлен с учетом мнений всех экспертов. Для комплексной оценки качества подъемно-транспортных машин в целом используют также интегральный показатель качества по ГОСТ 22732-77, равный отношению суммарного полезного эффекта П4 от использования крана к приведенным затратам. Например, для перегрузочных портальных кранов J=m1 П4m2 Кгm3/Mm4Nдm5, где П4 – часовая производительность; Кг – коэффициент готовности, представляющий собой среднее относительное время пребывания машин в работоспособном состоянии в предельном стационарном режиме эксплуатации; М – масса крана; Nд – общая мощность двигателей; m1 = 0,24; m2 = 0,972; m3 = 0,685; m4 = 0,522; m5 = 0,025. Показатель m2 по абсолютному значению наибольший из (m2 ... m5), т.е. при оптимальном проектировании перегрузочных кранов важнейшим - являются параметры, изменение которых в наибольшей степени влияет на производительность крана. Задача об оптимизации марки материала для крановой стрелы. Масса оптимально спроектированной коробчатой стрелы обратно пропорциональна корню из допускаемого напряжения [s] (в дальнейшем это будет доказано). С увеличением [s] масса стрелы mС уменьшается (рис.2.6, кривая 1), наименьшее значение ее будет при наибольшем рассматриваемом [s]. Но здесь не учтено дополнительное нагружение стрелы деформационным моментом.
Можно сформулировать следующие положения:
2. В зависимости от постановки задачи оптимизации и выбранной целевой функции могут быть получены разные оптимальные решения, т.е. разные значения оптимальных параметров. Ограничения
Для формирования множества вариантов объекта, на котором производят поиск оптимального решения, необходимо правильно разработать и учесть различные ограничения. Ограничения математически выражают те или иные связи, наложенные на объект оптимизации, и могут быть записаны в виде равенства: j = 0 (5.1) или в виде неравенства: j < 0, j > 0 (5.2) или в виде нестрогого неравенства: j где j - некоторая функция от параметров, которая так же, как и критерии качества, может быть задана либо аналитическим выражением, либо замкнутым алгоритмом определения. Введение ограничений позволяет учесть реальные условия и изготовления и функционирования объекта оптимизации с тем, чтобы оптимизация была физически осуществима. Ограничения на параметры часто задают в виде диапазонов значений параметров либо в виде совокупности их дискретных значений, либо в форме строгих или нестрогих неравенств. Так, при поиске оптимальной высоты h0 сечения коробчатой балки мостового крана необходимо ввести ограничение j = h0 – [h] Для сочлененных стрел портальных кранов (см. рис.2.3,б) можно записать следующие ограничения на параметры: j1=Х1 - DR=0; j2=Х3 – H j5=X9 – A2 Здесь в ограничениях j1= 0 и j2 В ограничении j6 В приведенных примерах ограничения в виде равенства или неравенства, как правило, могут быть явно разрешены относительно тех или иных параметров. Часто встречаются ограничения, неразрешимые в явном виде относительно параметров. Примерами могут быть уравнения совместности деформаций (например, канонические уравнения метода сил) при оптимизации статически неопределенных систем, условия замкнутости или условия проворачиваемости при оптимизации шарнирных механизмов и т.д. Ограничения по прочности при оптимизации коробчатых сечений крановых металлических конструкций. Проектировочный расчет крановых конструкций обычно производят на прочность от наибольших нагрузок II расчетного случая по их расчетным комбинациям. Для стрел поворотных кранов принимают следующие комбинации нагрузок: IIа - вес конструкции, вес груза при коэффициенте динамичности jII (работает механизм подъема); IIb1 или IIb2 – вес конструкции, вес груза, грузовые канаты отклонены от вертикали на угол aII в плоскости качания стрелы в сторону увеличения вылета (IIb1) или его уменьшения (IIb2) (неустановившееся движение механизма изменения вылета); IIс – вес конструкции, вес груза, канаты отклонены от вертикали на угол bII перпендикулярно плоскости качания стрелы (неустановившееся движение механизма поворота). Ограничение по прочности для наихудшей из комбинаций IIа , IIb1 или IIb2 : j1 = Мz 1 /Wz + N1/ F – [s] по комбинации IIc: j2 = Mz 2 /Wz + My 2 / Wy + N2 / F – [s] Здесь Мz 1 , N1 - вертикальный изгибающий момент и сжимающая сила в сечении по наихудшей комбинации нагрузок в плоскости качания стрелы; Mz 2, N2 – вертикальный и горизонтальный изгибающие моменты и сжимающая сила по комбинации нагрузок, включающей боковые нагрузки; Wz, My, F - моменты сопротивления и площадь сечения; [s] – допускаемое напряжение. В более полной постановке задачи вводят также ограничения по местной устойчивости поясов и стенок, в составе сечения учитывают ребра жесткости и вводят ограничения на их размещение и количество, предписывают соответствие толщин листов сортаменту и т. д. Ограничения на критерии качества обычно задаются в виде неравенств и относятся к критериям качества, дополнительно учитываемым при оптимизации по выработанной целевой функции. Примеры таких ограничений: по прогибу и времени затухания колебаний при оптимизации параметров крановых мостов, по отклонению траектории груза от горизонтали и грузовому неуравновешенному моменту при оптимизации стреловых систем кранов и т.д. В таких случаях иногда говорят, что дополнительные критерии качества переведены в разряд ограничений. Каждое ограничение в виде равенства, накладываемое на параметры или критерии качества, уменьшает на единицу размерность задачи оптимизации, т. е. число параметров, определяемых из условия экстремума целевой функции. Если число параметров равно числу ограничений в виде равенства, то оптимизация сводится к решению системы ограничений относительно всех параметров; если ограничения совместны, то решение существует, а если несовместны, то решения нет. Если число n –параметров больше числа m независимых ограничений в виде равенства, то возможно оптимальное определение (n – m) параметров. Наконец, если число независимых ограничений в виде равенства превышает число параметров, то также возможна оптимизация, однако это является особым, не рассматриваемым здесь случаем и требует специальных подходов к формированию целевой функции.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 1807; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.118 (0.018 с.) |


 i = 1,2,... N. (3.3)
i = 1,2,... N. (3.3) объекта, доставляющие экстремум целевой функции q, т.е. найти
объекта, доставляющие экстремум целевой функции q, т.е. найти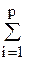 aiqi, (4.3)
aiqi, (4.3) ai – так называемый коэффициент весомости, отражающий важность, значимость i- го критерия качества, причем
ai – так называемый коэффициент весомости, отражающий важность, значимость i- го критерия качества, причем wi J = 2 p2, где p - число показателей. Коэффициент весомости i - го показателя вычисляют по формуле
wi J = 2 p2, где p - число показателей. Коэффициент весомости i - го показателя вычисляют по формуле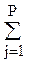 wij
wij  wij 2p2
wij 2p2 7.
7. =wij
=wij
 С учетом этого дополнительного нагружения получим изменение массы по кривой 2, часто имеющей минимум при некотором [s]. Наконец, различные значения [s] требуют различных марок стали (Ст.3, 09Г2С, 10ХСНД), различающихся по стоимости одной тонны. Кривая 3 (стоимость конструкции С) не будет непрерывной; при это наименьшее значение стоимости не совпадает по [s] с минимумом массы по кривой 2 и с наименьшим значением массы по кривой 1. Как показывает анализ, оптимальной по стоимости стрелы будет сталь 09Г2С.
С учетом этого дополнительного нагружения получим изменение массы по кривой 2, часто имеющей минимум при некотором [s]. Наконец, различные значения [s] требуют различных марок стали (Ст.3, 09Г2С, 10ХСНД), различающихся по стоимости одной тонны. Кривая 3 (стоимость конструкции С) не будет непрерывной; при это наименьшее значение стоимости не совпадает по [s] с минимумом массы по кривой 2 и с наименьшим значением массы по кривой 1. Как показывает анализ, оптимальной по стоимости стрелы будет сталь 09Г2С. 1. Критерии качества с изменением параметров объекта могут измениться как непрерывно, так и дискретно.
1. Критерии качества с изменением параметров объекта могут измениться как непрерывно, так и дискретно. 0, (5.3)
0, (5.3) 0; j3=X2 - R1
0; j3=X2 - R1 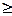 0; j6=X8 – D1
0; j6=X8 – D1 


