
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы нелинейного программированияСодержание книги
Поиск на нашем сайте
Общего метода решения нелинейных задач оптимизации пока не существует. Развитие нелинейного программирования сводилось к разработке частных алгоритмов, среди которых выделяются наиболее типичные. На эффективность того или иного метода оптимизации в задачах нелинейного программирования оказывают влияние: 1) вид целевой функции в окрестности экстремума и вообще в исследуемой области; 2) размерность задачи (число оптимизируемых параметров); 3) принятый шаг изменения оптимизируемых параметров в ходе решения; 4) требуемая точность определения оптимальных параметров. Для рассмотрения некоторых известных методов поиска параметров, доставляющих экстремум (в дальнейшем для определенности – минимум) нелинейных целевых функций, введем понятие о линиях (поверхностях) уровня функции.
Рис.2.10. К расчету статически неопределимой рамы
Пусть имеется непрерывная функция двух переменных Т а б л и ц а 3.
Конечно, в реальных задачах подобная таблица никогда не бывает заранее известна, в противном случае оптимальные значения параметров можно было бы установить непосредственно по ее данным; в нашем примере (см. табл. 3) это Пользуясь табл. 3 и в необходимых случаях интерполяцией, построим (рис. 2.11,а) кривые
Рис. 2.11. Линии поверхностей уровня
Для функций трех переменных можно построить поверхности уровня Если в исследуемой области функция имеет единственный экстремум, то поверхности уровня располагаются вокруг точки с координатами, отвечающими этому экстремуму (см. рис. 2.11,а, табл. 3). Функция с поверхностями уровня, подобными показанным на рис. 2.11,б, имеет два локальных экстремума (в общем случае – несколько экстремумов), причем эти экстремальные значения функции, вообще говоря, не совпадают между собой, и действительным (глобальным) экстремумом является какой-то один. В зависимости от начальной точки выбранного вычислительного процесса и принятой стратегии поиска мы найдем параметры, доставляющие либо глобальный экстремум, либо один из локальных, и для суждения о характере полученного результата нужны дополнительные исследования.
Наконец, если линии уровня в исследуемой области не замкнуты (рис. 2.11,в), то это означает, что экстремум функции (точнее ее наибольшее или наименьшее значение, когда производные от функции по параметрам не обращаются в нуль) отвечает точке, лежащей на границе области. Как уже отмечалось, форма поверхностей уровня обычно заранее не известна, если только она не ясна из физического смысла задачи или не исследовалась специально. Если данных о поведении функции в допустимой области нет, то поиск оптимальных параметров на компьютере ведут "вслепую". Понятны сопряженные с этим трудности и недостатки. Поэтому полезно, приступая к разработке алгоритма оптимизации, предварительно изучить поведение функции, выяснить форму поверхностей уровня и по возможности понять физические причины, лежащие в основе этих обстоятельств. Ниже рассматриваются некоторые типовые методы поиска экстремума нелинейной функции. Следует еще раз подчеркнуть, что ни один из них не является универсальным. Поэтому в практике оптимального проектирования конструкций подъемно-транспортных и строительных машин иногда удается применить эти типовые алгоритмы, но нередко приходится разрабатывать специальные алгоритмы оптимизации, отвечающие конкретным особенностям объектов, целевых функций и ограничений. Примерами таких специальных алгоритмов являются разработанные на кафедре ПТСМ СПбГТУ алгоритмы оптимизации параметров коробчатых сечений стрел и хоботов портальных кранов, включающих ребра жесткости, алгоритмы оптимального проектирования металлических конструкций балочных и шпренгельных стрел, порталов, стрел одноковшовых экскаваторов и т.д.
 , где , где  – размерность задачи. Известно применение этого метода для минимизации массы пролетного строения козлового крана; процесс оптимизации пяти параметров на компьютере занял примерно два часа. – размерность задачи. Известно применение этого метода для минимизации массы пролетного строения козлового крана; процесс оптимизации пяти параметров на компьютере занял примерно два часа.
Метод перебора может быть рекомендован для предварительного изучения изменчивости целевой функции по параметрам в исследуемой области.
 Метод локального поиска на координатной сетке (рис. 2.13). В начальной точке определяют значение функции. Затем все Метод локального поиска на координатной сетке (рис. 2.13). В начальной точке определяют значение функции. Затем все  параметров увеличиваются и уменьшаются на заданные малые числовые величины. В результате этого получают параметров увеличиваются и уменьшаются на заданные малые числовые величины. В результате этого получают  вариантов, лучший из которых принимают в качестве исходного для следующей итерации. Локальный поиск позволяет резко сократить число измерений функции по сравнению с методом перебора. При наличии нескольких локальных экстремумов метод приводит к одному из них в зависимости от выбранного начального приближения. вариантов, лучший из которых принимают в качестве исходного для следующей итерации. Локальный поиск позволяет резко сократить число измерений функции по сравнению с методом перебора. При наличии нескольких локальных экстремумов метод приводит к одному из них в зависимости от выбранного начального приближения.
Из векторной алгебры известно, что градиент скалярной функции направлен в сторону наискорейшего увеличения функции и что он ортогонален поверхности уровня, проходящей через данную точку. Вектор, противоположный градиенту (антиградиент), направлен в сторону наискорейшего уменьшения функции.
 по градиентному методу (рис. 2.14). В начальной точке численно определяют частные производные целевой функции по градиентному методу (рис. 2.14). В начальной точке численно определяют частные производные целевой функции  где где 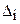 - малое приращение параметра - малое приращение параметра  ; затем выполняют шаг по антиградиенту, т.е. значения параметров в следующей итерации принимают согласно зависимостям ; затем выполняют шаг по антиградиенту, т.е. значения параметров в следующей итерации принимают согласно зависимостям  где где  - номер последней итерации; - номер последней итерации;  ; ;  - число параметров; - число параметров;  - коэффициент пропорциональности. После перехода к измененным значениям параметров вновь определяют составляющие градиента и совершают следующий шаг и так далее, пока все производные не окажутся меньше некоторой заранее заданной величины. - коэффициент пропорциональности. После перехода к измененным значениям параметров вновь определяют составляющие градиента и совершают следующий шаг и так далее, пока все производные не окажутся меньше некоторой заранее заданной величины.
 Метод наискорейшего спуска (рис. 2.15). Является модификацией градиентного метода и состоит в том, что при поиске минимума функции движение по антиградиенту, определенному в исходной точке, совершается до тех пор, пока функция в данном направлении убывает, после чего градиент вычисляют вновь до достижения заданной малой величины всех составляющих градиента. Итерационная формула процесса: Метод наискорейшего спуска (рис. 2.15). Является модификацией градиентного метода и состоит в том, что при поиске минимума функции движение по антиградиенту, определенному в исходной точке, совершается до тех пор, пока функция в данном направлении убывает, после чего градиент вычисляют вновь до достижения заданной малой величины всех составляющих градиента. Итерационная формула процесса:  где где  ; ;  - число параметров; - число параметров;  - номер точки, в которой определен градиент; - номер точки, в которой определен градиент;  - номер итерации, осуществляемой на данном направлении. - номер итерации, осуществляемой на данном направлении.
Градиентный метод и в особенности метод наискорейшего спуска обычно имеют более короткие траектории поиска, нежели локальный поиск на координатной сетке, однако требуют вычисления частных производных функции по параметрам. Их эффективность проявляется при большем удалении начальной точки от конечной и при меньшем числе параметров.
Список литературы
1. Вентцель Е.С. Исследование операций: Задачи, принципы, методология. М.: Наука, 1980. 208 с. 2. Троицкий В.А., Петухов Л.В. Оптимизация формы упругих тел. М.: Наука, 1982. 432 с. 3. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация/ Пер. с англ. М.: Мир, 1985. 509 с. 4. Реклейтис Г., Рейвиндран А., Рэгсдел К. Оптимизация в технике: В 2 кн./ Пер. с англ. М.: Мир, 1986. 5. Брауде В.И., Тер-Мхитаров М.С. Системные методы расчета грузоподъемных машин. Л.: Машиностроение, 1985. 181 с. 6. Букреев В.В. Расчет и конструирование строительных и дорожных машин. Оптимизация металлоконструкций на примере стрелы экскаватора: Лаб. практикум. СПб.: Изд-во СПбГТУ, 1998. 26 с. 7. Справочник по кранам. Т.1/ Под ред. М.М. Гохберга. Л.: Машиностроение, 1988. 536 с. 8. Справочник по кранам. Т.2/ Под ред. М.М. Гохберга. Л.: Машиностроение, 1988. 559 с.
Оглавление
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.119.149 (0.011 с.) |


 при ограничениях
при ограничениях  ,
,  . Также, пусть известна таблица значений функции
. Также, пусть известна таблица значений функции  (табл. 3).
(табл. 3).
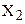

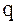
 ,
,  (с точностью до целых),
(с точностью до целых), 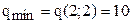 .
. в осях
в осях 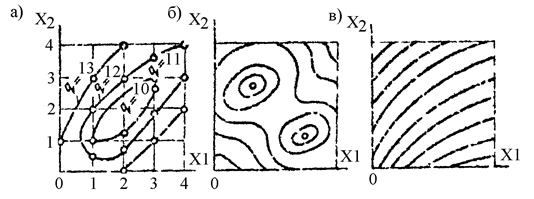
 в осях
в осях  . При числе переменных более трех говорят о поверхностях уровня в многомерном пространстве (или о гиперповерхностях уровня).
. При числе переменных более трех говорят о поверхностях уровня в многомерном пространстве (или о гиперповерхностях уровня). Метод перебора на координатной сетке (рис. 2.12). Разделив принятые интервалы изменения всех параметров на некоторое число частей, определяют значения целевой функции при всех возможных сочетаниях значений каждого из параметров (т.е. во всех узлах координатной сетки) и выбирают из них то, которое для достаточно гладкой функции и при достаточно малом шаге изменения переменных будет близко к искомому экстремуму.
Метод перебора на координатной сетке (рис. 2.12). Разделив принятые интервалы изменения всех параметров на некоторое число частей, определяют значения целевой функции при всех возможных сочетаниях значений каждого из параметров (т.е. во всех узлах координатной сетки) и выбирают из них то, которое для достаточно гладкой функции и при достаточно малом шаге изменения переменных будет близко к искомому экстремуму. Градиентный метод. Градиентом функции называют вектор, проекции которого на координатные оси равны частным производным функции по соответствующим координатам. Для функции трех переменных
Градиентный метод. Градиентом функции называют вектор, проекции которого на координатные оси равны частным производным функции по соответствующим координатам. Для функции трех переменных  , где
, где  - единичные векторы, ориентированные по соответствующим осям.
- единичные векторы, ориентированные по соответствующим осям.


